今天学了了强连通算法
Tarjan算法
Tarjan算法是一种求解有向图强连通分量的线性时间的算法,他运用到了DFS算法以及DFS的特性和数据结构——栈。
算法介绍:如果两个顶点可以相互通达,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
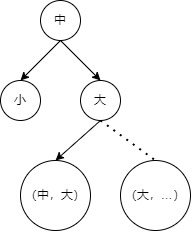
举一个列子,如下图所示:

这是一个有向图,我们可以了解到该图有4给个强连通分量,分别是{A,B,C},{D},{E},{F}.
首先我们需要使用存储图的办法,这边有俩个一个是邻接表,一个是邻接矩阵。我这里使用的是邻接矩阵。
这个算法使用到了DFS算法,我们设立一个时间戳,每访问一个节点给他一个时间,这里我们需要俩个全局变量——dfn、low以及一个栈。
在调用dfs函数的时候我们把该点入栈,时间戳++,然后遍历该点可以继续走下去的点,去遍历他。同时我们要看遍历下去的点里面的low值是不是比当前节点的low值小,如果小,我们是需要更新当前节点的low值(这个稍后再解释)

这里A节点下前面的1表示dfn的值,而后面的表示low的值,我们可以发现A点可以走的点为B,E,由于dfs的特性,我们会先走到B点,B点的时间戳是2,dfn和low数组的值分别是2,2.
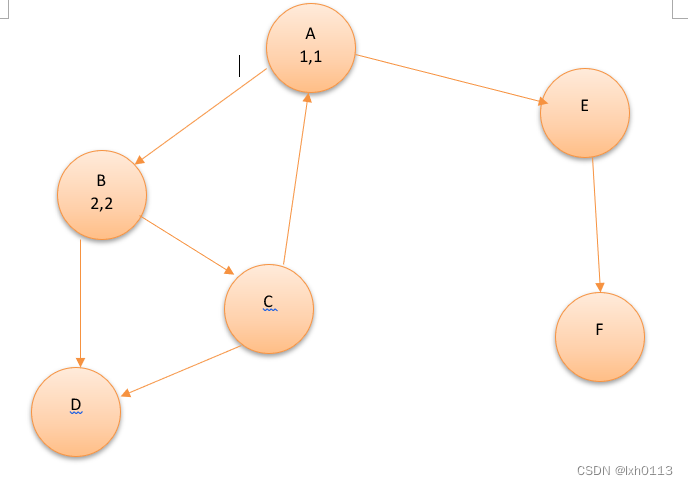
然后会从B遍历到C,D,我们到C会更新到3,3,同理D的值也会变成4,4。
D点此时是没有可以继续往下的值了,此时我们需要判断当前dfn的值是否对应low的值,这个和并查集有点相似,是看它的祖先,很明显D点是自己一个人构成环,所以D点出栈。

然后可以从C到的点还有A点,此时A点是已经访问过的节点,所以我们需要判断它是否还在栈里面,我们发现是的,于是我们执行low[x]=min(low[x],low[y]),我们需知道此时y也就是A节点的low值是1,所以我们需要给C点low赋值为1,因为C能够通往还在栈中的点说明是构成了强连通分量。
然后我们会返回到B点,B点其实也执行完了C点的dfs,下面要执行low[x]=min(low[x],low[y]),此时y的值是C点,C点的low已经变成了1,那么B点也相应的变成了1.

B点会接下来到D点我们会发现D点已经被访问过了,而且D也不再栈里面了,我们不执行任何操作。
这个时候该返回了,返回到B,此时B需要访问D,我们发现D已经走过,我们就需要再判D此时是否还在栈里面,我们发现上面的时候D已经出栈了,所以不执行任何操作,继而返回到A点。
此时A点深搜完了B点,会继续到E点,(下面是一样的了)搜到E赋值dfn为5,low为5……
最后会变成:

我们最后会全部出栈,每一次出栈都会找low值一样的一起出栈,是代表他们同属于一个强连通分量。
C代码如下:
//tarjan算法
#include<stdio.h>
#define N 100
int e[N][N],book[N];
int n,m,time;
int stack[N],top,dfn[N],low[N];
int min(int a,int b)
{
if(a>b) return b;
return a;
}
int fd(int x)
{
int i;
for(i=0;i<top;i++)
{
if(x==stack[i]) return 1;
}
return 0;
}
int tarjan(int x)
{
dfn[x]=low[x]=++time;
stack[top++]=x;
int i,k;
for(i=1;i<=n;i++)
{
if(e[x][i]&&dfn[i]==0)
{
tarjan(i);
low[x]=min(low[x],low[i]);
}
else if(e[x][i]&&dfn[i]&&fd(i))
{
low[x]=min(low[x],low[i]);
}
}
if(dfn[x]==low[x])
{
k=low[x];
while(low[stack[--top]]==k&&top>=0)
{
printf("%d ",stack[top]);
}
top++;
puts("");
}
return 0;
}
int main()
{
int i,x,y;
puts("请输入顶点个数:");
scanf("%d",&n);
puts("请输入边的个数:");
scanf("%d",&m);
puts("请输入哪些顶点是可以连通的:");
for(i=0;i<m;i++)
{
scanf("%d%d",&x,&y);
e[x][y]=1;
}
tarjan(1);
return 0;
}C++代码如下:
//tarjan算法
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int e[N][N],book[N];
int n,m,t;
int s[N],top,dfn[N],low[N];
int min(int a,int b)
{
if(a>b) return b;
return a;
}
int fd(int x)
{
int i;
for(i=0;i<top;i++)
{
if(x==s[i]) return 1;
}
return 0;
}
int tarjan(int x)
{
dfn[x]=low[x]=++t;
s[top++]=x;
int i,k;
for(i=1;i<=n;i++)
{
if(e[x][i]&&dfn[i]==0)
{
tarjan(i);
low[x]=min(low[x],low[i]);
}
else if(e[x][i]&&dfn[i]&&fd(i))
{
low[x]=min(low[x],low[i]);
}
}
if(dfn[x]==low[x])
{
k=low[x];
while(low[s[--top]]==k&&top>=0)
{
printf("%d ",s[top]);
}
top++;
puts("");
}
return 0;
}
int main()
{
int i,x,y;
cout << "请输入顶点个数:" << endl;
cin >> n ;
cout << "请输入边的个数:" << endl;
cin >> m ;
cout << "请输入哪些顶点是可以连通的:" << endl;
for(i=0;i<m;i++)
{
cin >> x >> y ;
e[x][y]=1;
}
tarjan(1);
return 0;
}