701 二叉搜索树的插入操作 medium

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

如果要按照题目中所说改变二叉树的原本结构来解决这道题，那这道题就会变得有些复杂。

所以，按照题意，遍历二叉树，找到空结点插入值就可以了。无论如何都可以找到一个叶子结点，满足待插入的结点要求（大于或小于当前叶子结点）。

如果使用递归法，返回类型是空（因为最终还是要返回根节点），传入参数是当前遍历到的结点值和目标值；

终止条件是找到空结点，然后给当前空结点赋值，返回即可

每次递归的处理逻辑要根据二叉搜索树的特点，如果插入值大于当前结点，就往右子树遍历；插入值小于当前结点，就往左子树遍历。

代码如下：

TreeNode* pre = nullptr;
void reversal(TreeNode* cur, int val) {
    if (cur == nullptr) {
        TreeNode* node = new TreeNode(val);
        if (pre->val > val) pre->left = node;
        else pre->right = node;
        return;
    }
    pre = cur;
    if (cur->val > val) reversal(cur->left, val);
    if (cur->val < val) reversal(cur->right, val);
    return;
}
TreeNode* insertIntoBST(TreeNode* root, int val) {
    pre = new TreeNode(0);
    if (root == nullptr) {
        TreeNode* node = new TreeNode(val);
        root = node;
    }
    reversal(root, val);
    return root;
}

这道题使用迭代法会更明了一些，先找到空结点，然后根据前一个结点值的大小判断插入位置就好了，代码如下：

TreeNode* insertIntoBST(TreeNode* root, int val) {
    if (root == nullptr) {
        TreeNode* node = new TreeNode(val);
        return node;
    }
    TreeNode* pre = root;
    TreeNode* cur = root;
    while (cur != nullptr) {
        pre = cur;
        if (cur->val > val) cur = cur->left;
        else cur = cur->right;
    }
    TreeNode* node = new TreeNode(val);
    if (pre->val > val) pre->left = node;
    else pre->right = node;

    return root;
}

---

450 删除二叉搜索树中的结点 medium

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1、首先找到需要删除的节点；
2、如果找到了，删除它。

这道题，找到要删除的结点并不难，关键是如何删除目标结点。

所以如果采用递归法找结点，关键就在于终止条件

终止条件第一步，遍历结点值一定等于目标值

终止条件第二步：

• 如果该结点是叶子结点，最简单，直接删掉，返回空结点就行；

• 如果该结点左孩子为空，就要把右孩子返回（同样满足二叉搜索树）

• 如果该结点右孩子为空，就要把左孩子返回（同样满足二叉搜索树）

• 如果该结点左右孩子都不为空，理论上肯定要用右孩子顶替当前结点，但关键问题在于如果右孩子还有左孩子（可恶的孙子），参见下图：

  

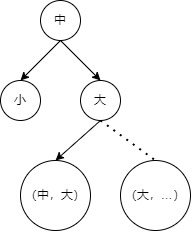
  如果要删除（中）结点，（中）结点的左右子树都存在，从小到大还剩下

  （小）， （中，大），（大），（大，…）四个结点，代码随想录的方法是把（小）结点移动到（中，大）的左孩子，然后用（大）结点替代（中）结点。

整体代码如下：

TreeNode* deleteNode(TreeNode* root, int key) {
    if (root == nullptr) return root;
    if (root->val == key) {
        if (root->left == nullptr && root->right == nullptr) {
            delete root;
            return nullptr;
        }
        else if (root->left != nullptr && root->right == nullptr) {
            auto temp = root->left;
            delete root;
            return temp;
        }   
        else if (root->left == nullptr && root->right != nullptr) {
            auto temp = root->right;
            delete root;
            return temp;
        }
        else {
            auto node = root->right;
            // 关键点，要一直找，找到最左侧的结点
            while (node->left != nullptr) 
                node = node->left;
            node->left = root->left;
            TreeNode* temp = root;
            root = root->right;
            delete temp;
            return root;
        }
    }
    // 找到目标结点
    if (root->val > key) root->left = deleteNode(root->left, key);
    if (root->val < key) root->right = deleteNode(root->right, key);

    return root;
}

使用delete命令的目的是令代码更规范，除了随想录中的写法，只要合理都可以。

本道题同样可以使用迭代法，代码直接参考随想录中的写法：

private:
    // 将目标节点（删除节点）的左子树放到 目标节点的右子树的最左面节点的左孩子位置上
    // 并返回目标节点右孩子为新的根节点
    // 是动画里模拟的过程
    TreeNode* deleteOneNode(TreeNode* target) {
        if (target == nullptr) return target;
        if (target->right == nullptr) return target->left;
        TreeNode* cur = target->right;
        while (cur->left) {
            cur = cur->left;
        }
        cur->left = target->left;
        return target->right;
    }
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        TreeNode* cur = root;
        TreeNode* pre = nullptr; // 记录cur的父节点，用来删除cur
        while (cur) {
            if (cur->val == key) break;
            pre = cur;
            if (cur->val > key) cur = cur->left;
            else cur = cur->right;
        }
        if (pre == nullptr) { // 如果搜索树只有头结点
            return deleteOneNode(cur);
        }
        // pre 要知道是删左孩子还是右孩子
        if (pre->left && pre->left->val == key) {
            pre->left = deleteOneNode(cur);
        }
        if (pre->right && pre->right->val == key) {
            pre->right = deleteOneNode(cur);
        }
        return root;
    }