折半查找概念

折半查找，也称为二分查找，是一种在有序数组中查找特定元素的高效算法。
其基本思想是：首先确定整个查找区间的中间位置，即 mid = (left + right) / 2，然后使用要查找的值 key 与中间位置的元素进行比较。
如果 key 等于中间元素，则查找成功，返回该元素的存储位置；
如果 key 大于中间元素，则在数组的右半部分继续查找；
如果 key 小于中间元素，则在数组的左半部分继续查找。
每次比较都使搜索范围缩小一半，因此查找效率较高。
需要注意的是，折半查找要求待查表为有序表，且插入和删除操作困难。

查找过程

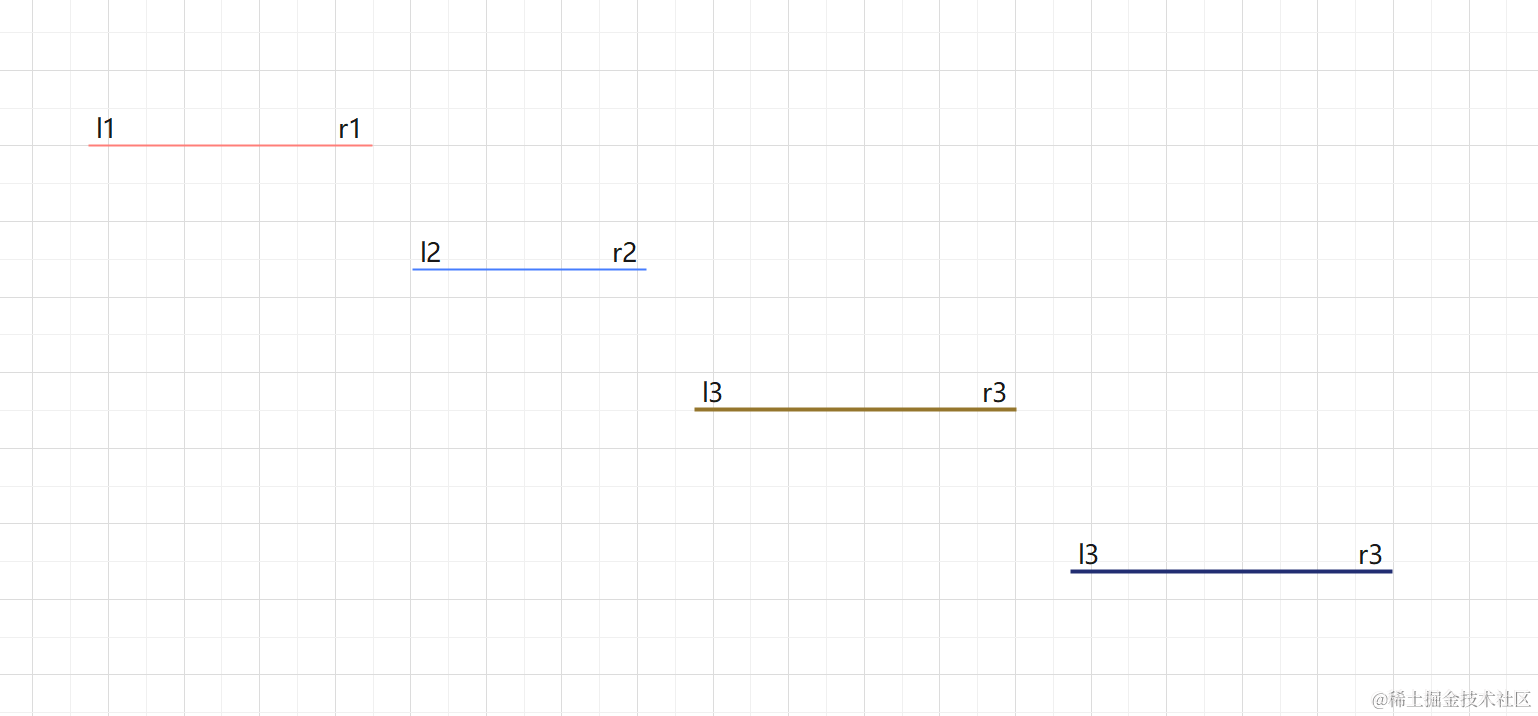
每次将待查记录所在的区间缩小一半
查找过程：

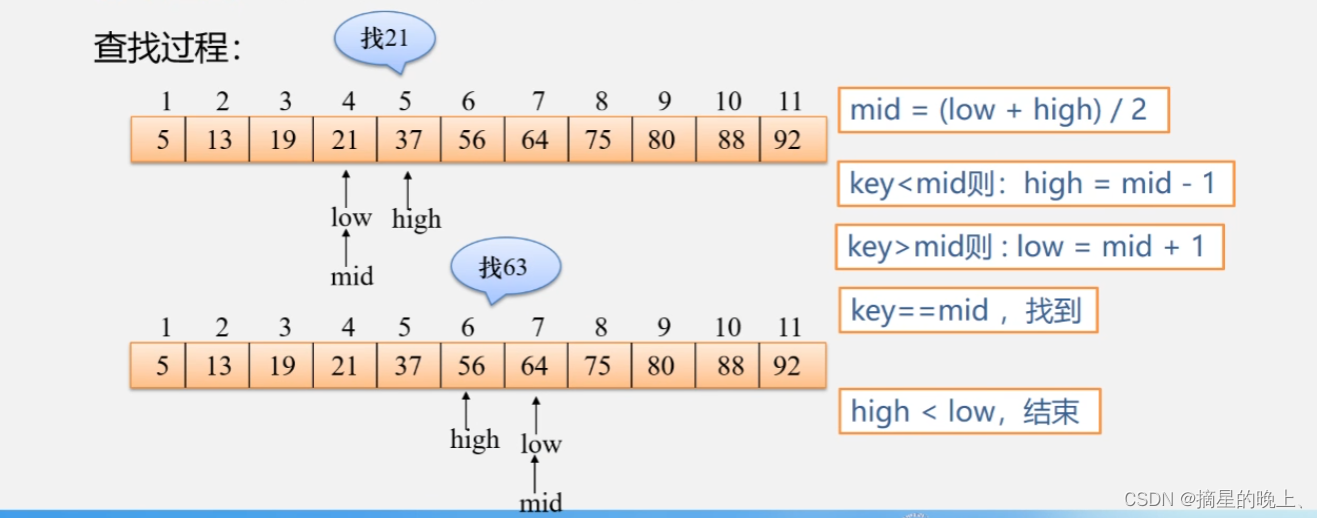
注意：在做查找的过程中，如果 low 指针和 high 指针的中间位置在计算时位于两个关键字中间，即求得 mid 的位置不是整数，需要统一做取整操作。

折半查找算法: (非递归算法)

设表长为n，low、high和mid分别指向待查元素所在区间的上界，下界和中点，key为给定的要查找的值

初始时，令low=1，high=n，mid=(low+high)/2
让k与mid指向的记录比较
若key==R[mid].key，查找成功
若key<R[mid].key，则 high=mid-1
若key>R[mid].key，则 low=mid+1
重复上诉操作，直到low>high时，查找失败。

算法的简单实现：

int Search_Bin (SSTable ST, KeyType key ){
	low = 1 ; // 置区间初值
	high = ST.length;
	while (low <= high) {
		mid = (low + high) / 2 ;
		if (ST.R[mid].key == key) return mid ; // 找到待查元素
		else if (key < ST.R[mid].key) //缩小查找区间
			high=mid-1;//继续在前半区间进行查找
		else low = mid + 1; // 继续在后半区间进行查找
	}
return 0;// 顺序表中不存在待查元素
} // Search Bin

折半查找法的性能分析

性能分析：

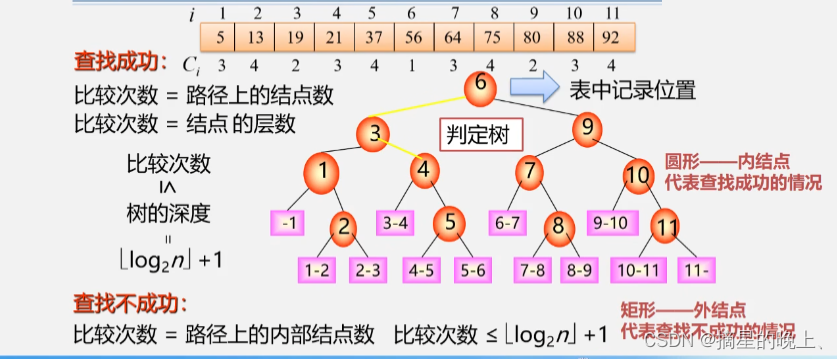
示例：

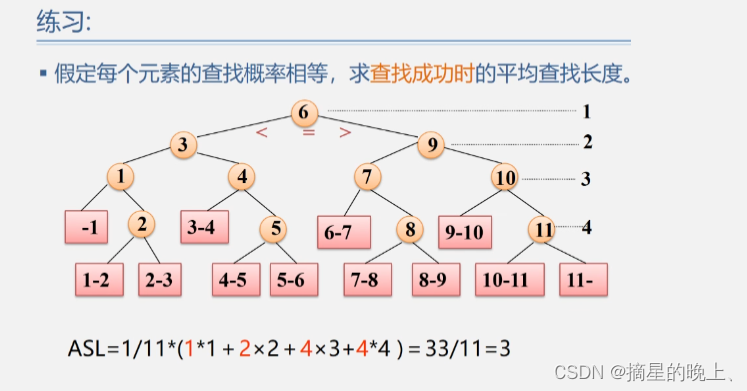
平均查找长度ASL：

成功时：

复杂度

折半查找的时间复杂度为 O(log2n)，折半查找的效率比顺序查找高，但折半查找只适用千有序表，且限于顺序存储结构

折半查找法的特点：

折半查找法的优点：效率比顺序查找高。比较次数少，查找效率高。
折半查找法的缺点：只是适用于有序表，且限于顺序存储结构，对链式表无效。对表结构要求高，只能用于顺序存储的有序表。
如果对无席表进行二分查找，查找前需要排序，而排序本身是一种费时的运算，同时为了保持顺序表的有序性，对有序表进行插入和别除时，平均比较和移动表中一半元素，这也是一种费时的运算。因此，折半查找不适用于数据元素经常变动的线性表。

参考资料：数据结构与算法基础-王卓老师