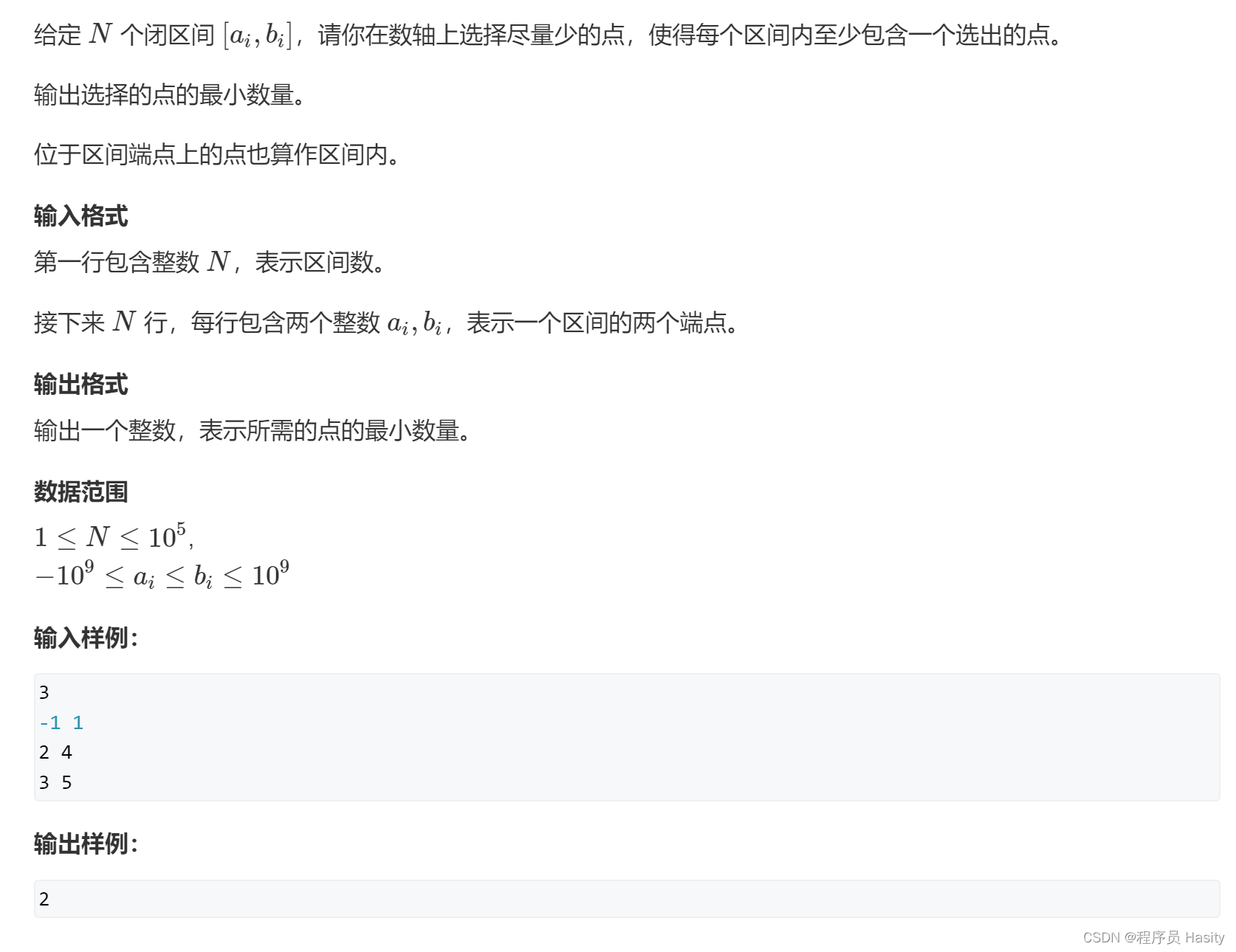
905. 区间选点

思路

（贪心）O(nlogn)

根据右端点排序

1. 将区间按右端点排序

2. 遍历区间，如果当前区间左端点不包含在前一个区间中，则选取新区间，所选点个数加1，更新当前区间右端点。如果包含，则跳过。

3. 输出所选点的个数。

举例: 为什么不能根据左端点排序呢？

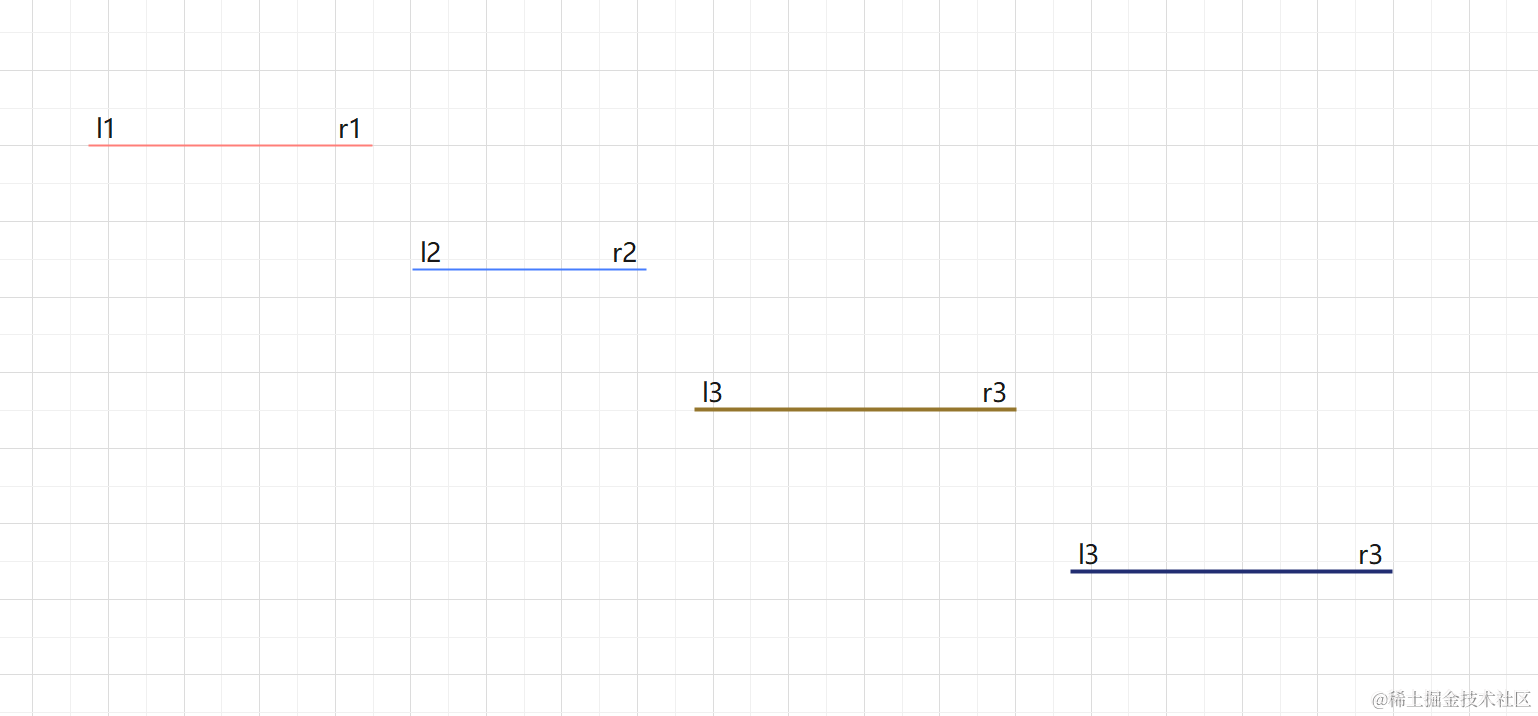
如下图所示，有三个区间

我们按右侧排序是如图所示，l3 > r2，点数加1，更新右端点，l1 < l3，无需更新，直接跳过

如果改成按左侧排序的话，r2 < r1 && r3 < r1,无需更新所需点数，输出点数为1（错误）。

• 第一个区间为l1~r1, 当我们遍历到l2~r2的时候，没有问题，l2 < r1, 无需更新。
• 但当我们遍历到l3~r3这个区间的话，就出现问题了，l3 < r1, 无需更新
• 输出点数1

解决办法 ：在遍历其他区间的时候，同时更新区间右端点取最小值

Java代码

import java.util.*;
class Range implements Comparable<Range>{
    int l,r;
    public Range(int l,int r){
        this.l = l;
        this.r = r;
    }
    public int compareTo(Range o){
        return Integer.compare(r,o.r);
        //return this.r - o.r;
    }
}
public class Main{
    static int N = 100010,INF = 0x3f3f3f3f,n;
    static Range[] range = new Range[N];//结构体创建数组需要定义成全局变量
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);

        n = scan.nextInt();
        for(int i = 0 ; i < n ; i ++ ){
            int l = scan.nextInt();
            int r = scan.nextInt();
            range[i] = new Range(l,r);
        }
        //结构体排序
        Arrays.sort(range,0,n); 
        //Arrays.sort(range, 0, n, (o1, o2) -> o1.r - o2.r);

        int res = 0;//表示一共需要多少点
        int ed = -INF; // 上一个点的右端点
        for(int i = 0 ; i < n ; i ++ ){
            if(range[i].l > ed){
                res ++ ;
                ed = range[i].r;
            }
        }
        System.out.println(res);
    }
}

根据左端点排序

import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        List<Pair> v = new ArrayList<>();
        for(int i = 0; i < n; i ++) {
            int l = sc.nextInt();
            int r = sc.nextInt();
            v.add(new Pair(l, r));
        }
        Collections.sort(v, (a, b) -> a.x - b.x);
        int l = Integer.MIN_VALUE;
        int r = Integer.MIN_VALUE;
        int res = 0;
        for(Pair p : v) {
            if(p.x <= r) {
                // l = Math.max(l, p.x);
                r = Math.min(r, p.y);   (每次取r的最小值，本质上其实还是根据右端点进行排序)
            } else {
                res += 1;
                l = p.x;
                r = p.y;
            }
                
        }
        System.out.println(res);
    }


}

class Pair implements Comparable<Pair> {
    int x;
    int y;
    public Pair(int x, int y) {
        this.x = x;
        this.y = y;
    }


    @Override
    public int compareTo(Pair o) {
        return Integer.compare(this.x, o.x);
    }
}

正确性证明 ：

定义：Ans 为所有可行方案中所需点最小数量，Cnt为当前方案中所需点的数量(一种可行方案)

1. 为证明 Ans == Cnt ，我们只需证明 Ans >= Cnt , Ans <= Cnt即可。

2. 既然Ans为最小数量，易得Ans <= Cnt。

3. 由于我们是根据右端点进行排序遍历，举一个极端例子，由图可知，Cnt等于4，Ans >= 4。

4. Ans >= Cnt &&Ans <= Cnt -> Ans = Cnt。