【C++】优先级队列priority

这里先简单介绍一下优先级队列priority_queue：优先队列是一种容器适配器,默认的情况下，如果没有为特定的priority_queue类实例化指容器类，则使用vector (deque 也是可以的),需要支持随机访问迭代器，以便始终在内部保持堆结构

文章目录

- 一、使用
- 二、仿函数
- 三、模拟实现
- - 1、基础接口
  - 2、push与向上调整
  - 3、pop与向下调整
  - 4、构造函数
  - 5、总体代码

一、使用

在有了前面容器使用的基础之下，我们对于优先级队列priority_queue的使用成本不是很大，值得注意的是头文件为

普通的队列是先进先出，优先级队列默认是优先级高的先出

Container:优先级队列默认使用vector作为其底层存储数据的容器，支持[]的使用，支持随机访问，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。

Compare:注意：默认情况下priority_queue是大堆，仿函数为less。

构造函数

接口

查看文档的接口

常用接口

函数声明	接口说明
priority_queue()/priority_queue(first, last)	构造一个空的优先级队列
empty( )	检测优先级队列是否为空，是返回true，否则返回 false
top( )	返回优先级队列中最大(最小元素)，即堆顶元素
push(x)	在优先级队列中插入元素x
pop()	删除优先级队列中最大(最小)元素，即堆顶元素

直接进入代码环节：

1.默认情况下，priority_queue是大堆

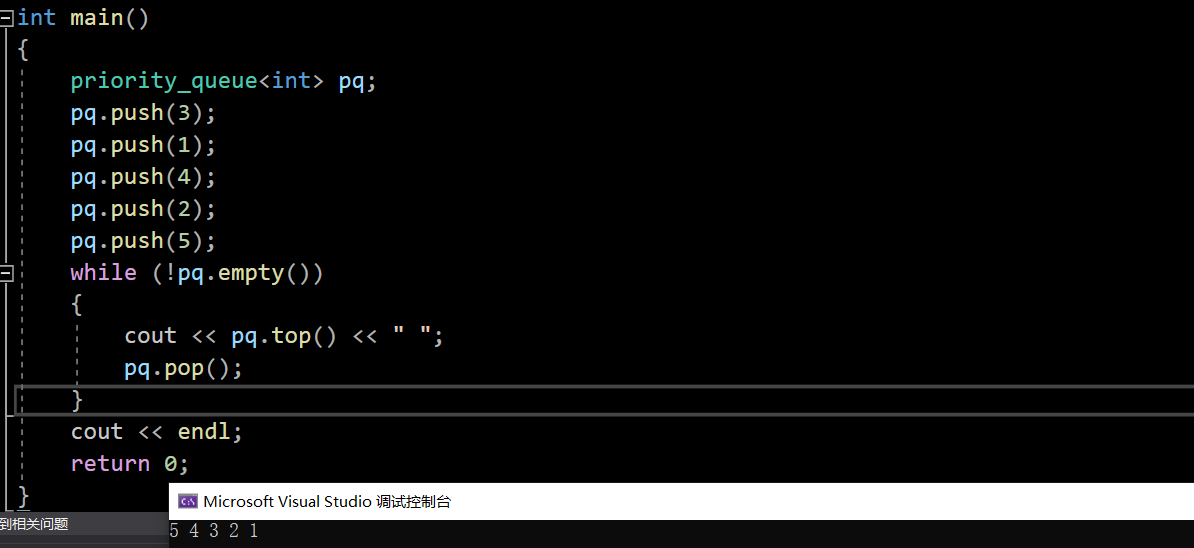
2.想让priority_queue是小堆:greater,头文件为functional

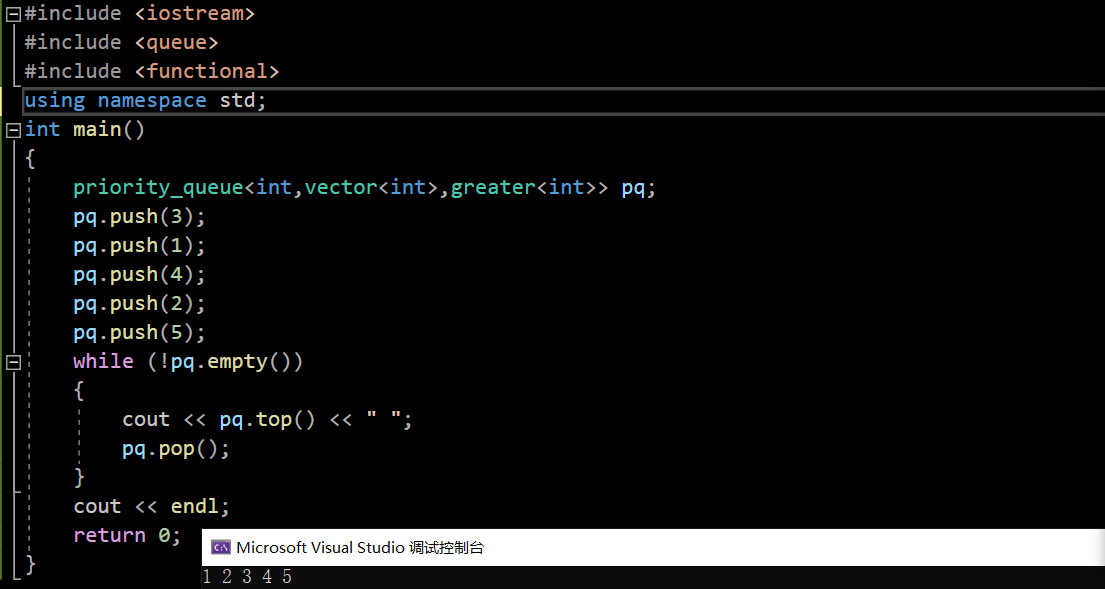
到了这里，我们发现priority_queue的使用并不难，下面，我们通过一道题目来看看priority_queue的妙处把：

数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

直接排序是O（NlogN），这个地方既可以建大堆也可以建小堆:建n个数的大堆，建堆是O(n),然后在pop K次，即O（N+k*logN），缺陷在于N太大。建K个数的小堆，剩下的数进一个数据与堆顶做比较，大的进堆，最终第K大的就是堆顶，建K个数的小堆为O（K），故时间复杂度为O（K+（N-K）*logK），当N远大于K是建议采用第二种。

第一种：建n个数的大堆

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        //建大堆
        priority_queue<int> pq(nums.begin(),nums.end());
        //前k-1个pop
        while(--k)
        {
            pq.pop();
        }
        return pq.top();
    }
};

第二种：建K个数的小堆

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        //前k个数建小堆
        priority_queue<int,vector<int>,greater<int>>pq(nums.begin(),nums.begin()+k);
        for(size_t i =k;i<nums.size();i++)
        {
            if(nums[i]>pq.top())
            {
                pq.pop();
                pq.push(nums[i]);
            }
        }
        return pq.top();
    }
};

我们可以发现在有了优先级队列之后我们对于这道题的解法大大简便了。不用像之前一样去自己手动实现一个堆了。

二、仿函数

仿函数/函数对象也是类，是一个类对象。仿函数要重载operator()，我们直接自己来通过代码来看一看仿函数：

namespace hwc
{
	template <class T>
	class less
	{
	public:
		bool operator()(const T& x, const T& y)
		{
			return x < y;
		}
	};
	template <class T>
	class greater
	{
	public:
		bool operator()(const T& x, const T& y)
		{
			return x > y;
		}
	};

}
int main()
{
	hwc::less<int> lessFunc;
	lessFunc(1, 2);
	return 0;
}
//lessFunc是一个对象，仿函数对象，可以像函数一样使用

仿函数的作用在于：在C语言中我们通过传入函数指针解决升序降序问题，虽然C++兼容了C，但是C++并没有继续利用函数指针，而是通过仿函数来控制升序和降序，我们直接以之前写过的排序为例子，通过利用仿函数来实现升序和降序：

template<class T,class Compare>
void BubbleSort(T* a, int n, Compare com)
{
	for (int j = 0; j < n; j++)
	{
		int exchange = 0;
		for (int i = 1; i < n - j; i++)
		{
			//if (a[i]<a[i-1])
			if (com(a[i], a[i-1]))
			{
				swap(a[i - 1], a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
		{
			break;
		}
	}
}
int main()
{
	hwc::less<int> lessFunc;
	hwc::greater<int> greaterFunc;
	lessFunc(1, 2);
	int a[] = { 2,3,4,5,6,1,2,8 };
    BubbleSort(a, sizeof(a) / sizeof(int),lessFunc);
	for (auto e : a)
	{
		cout << e << " ";
	}
	cout << endl;
	BubbleSort(a, sizeof(a) / sizeof(int), greaterFunc);
	for (auto e : a)
	{
		cout << e << " ";
	}
	cout << endl;

	return 0;
}

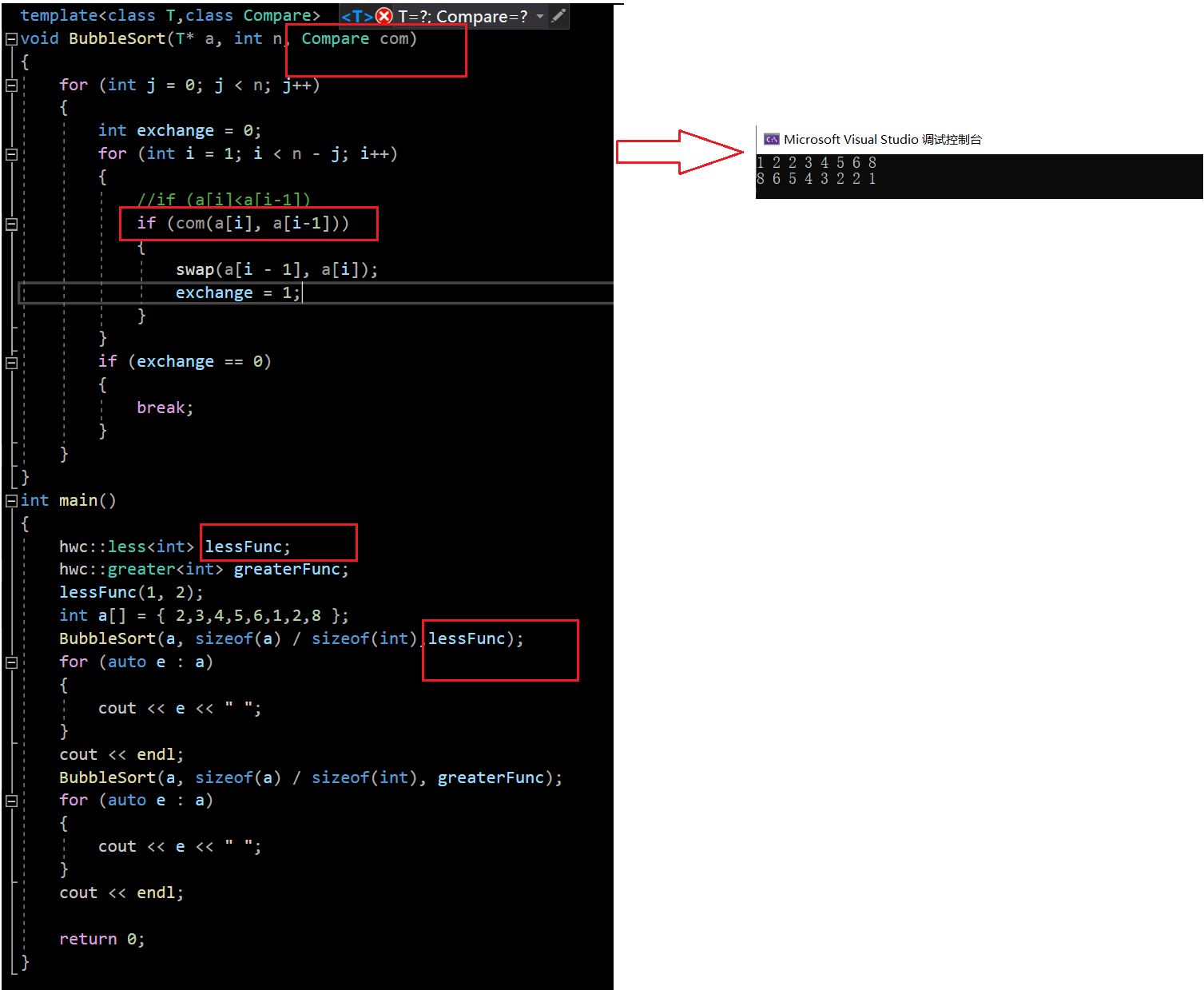
传值传参问题：这里是直接传值传参Compare com,当然也可以传引用传参const Compare& com,不过要记得加上const进行修饰，另外一般的仿函数比较小，问题不是很大。

自定义类型
这里的比较大小是比较常见的，如果是自定义类型：

比如日期类，那该如何去进行大小的比较？一种是重载大小的比较运算符，使之支持日期类的大小比较。另一种是可以自己定义仿函数专门去进行日期类的大小比较

1.重载运算符

比较大小需要我们自己去重载>,<,<<，这些在日期类的时候我们就详细的说过了，直接来看代码：

#include <iostream>
#include <queue>
#include <functional>
#include <algorithm>
#include <vector>


using namespace std;
class Date
{
public:
	Date(int year = 1900, int month = 1, int day = 1)
		: _year(year)
		, _month(month)
		, _day(day)
	{}
	bool operator<(const Date& d)const
	{
		return (_year < d._year) ||
			(_year == d._year && _month < d._month) ||
			(_year == d._year && _month == d._month && _day < d._day);
	}
	bool operator>(const Date& d)const
	{
		return (_year > d._year) ||
			(_year == d._year && _month > d._month) ||
			(_year == d._year && _month == d._month && _day > d._day);
	}
	friend ostream& operator<<(ostream& _cout, const Date& d)
	{
		_cout << d._year << "-" << d._month << "-" << d._day;
		return _cout;
	}
private:
	int _year;
	int _month;
	int _day;
};
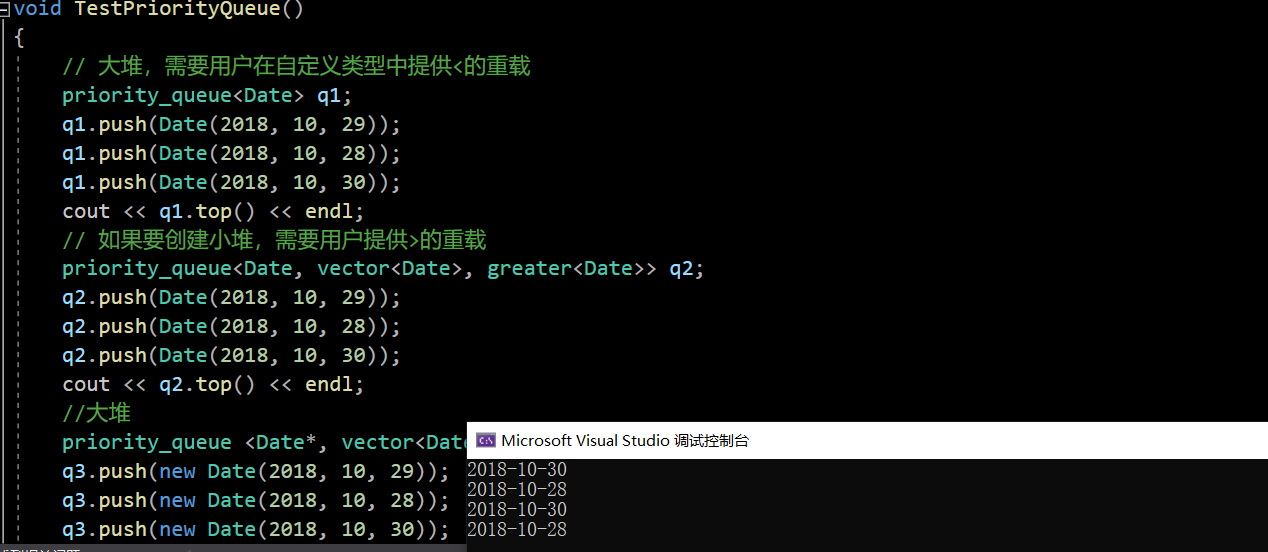
void TestPriorityQueue()
{
	// 大堆，需要用户在自定义类型中提供<的重载
	priority_queue<Date> q1;
	q1.push(Date(2018, 10, 29));
	q1.push(Date(2018, 10, 28));
	q1.push(Date(2018, 10, 30));
	cout << q1.top() << endl;
	// 如果要创建小堆，需要用户提供>的重载
	priority_queue<Date, vector<Date>, greater<Date>> q2;
	q2.push(Date(2018, 10, 29));
	q2.push(Date(2018, 10, 28));
	q2.push(Date(2018, 10, 30));
	cout << q2.top() << endl;
}
int main()
{
	TestPriorityQueue();
}

2.定义仿函数

如果传入的是Date*指针，此时上面的运算符重载已经不符合我们的需求了，比较的是地址的大小，但是我们要比较的是日期的大小，所以我们通过自己定义仿函数的方式来实现我们的需求：

class Date
{
public:
	Date(int year = 1900, int month = 1, int day = 1)
		: _year(year)
		, _month(month)
		, _day(day)
	{}
	bool operator<(const Date& d)const
	{
		return (_year < d._year) ||
			(_year == d._year && _month < d._month) ||
			(_year == d._year && _month == d._month && _day < d._day);
	}
	bool operator>(const Date& d)const
	{
		return (_year > d._year) ||
			(_year == d._year && _month > d._month) ||
			(_year == d._year && _month == d._month && _day > d._day);
	}
	friend ostream& operator<<(ostream& _cout, const Date& d)
	{
		_cout << d._year << "-" << d._month << "-" << d._day;
		return _cout;
	}
private:
	int _year;
	int _month;
	int _day;
};

struct PDateLess
{
	bool operator()(const Date* d1, const Date* d2)
	{
		return *d1 < *d2;
	}
};

struct PDateGreater
{
	bool operator()(const Date* d1, const Date* d2)
	{
		return *d1>*d2;
	}
};
void TestPriorityQueue()
{
    //大堆
	priority_queue <Date*, vector<Date*>, PDateLess> q3;
	q3.push(new Date(2018, 10, 29));
	q3.push(new Date(2018, 10, 28));
	q3.push(new Date(2018, 10, 30));
	cout << *q3.top() << endl;
	//小堆
	priority_queue<Date*, vector<Date*>, PDateGreater> q4;
	q4.push(new Date(2018, 10, 29));
	q4.push(new Date(2018, 10, 28));
	q4.push(new Date(2018, 10, 30));
	cout << *q4.top() << endl;
}

最终顺利完成：

有了上面的知识内容之后，下面我们进入的是优先级队列priority_queue的模拟实现！👇

三、模拟实现

1、基础接口

const T& top() const
{
    return _con[0];
}

bool empty() const
{
    return _con.empty();
}

size_t size() const
{
    return _con.size();
}

2、push与向上调整

优先级队列就是堆结构，插入一个数之后，我们还需要去进行向上调整

void push(const T& x)
{
    _con.push_back(x);
    adjust_up(_con.size() - 1);
}

向上调整算法：

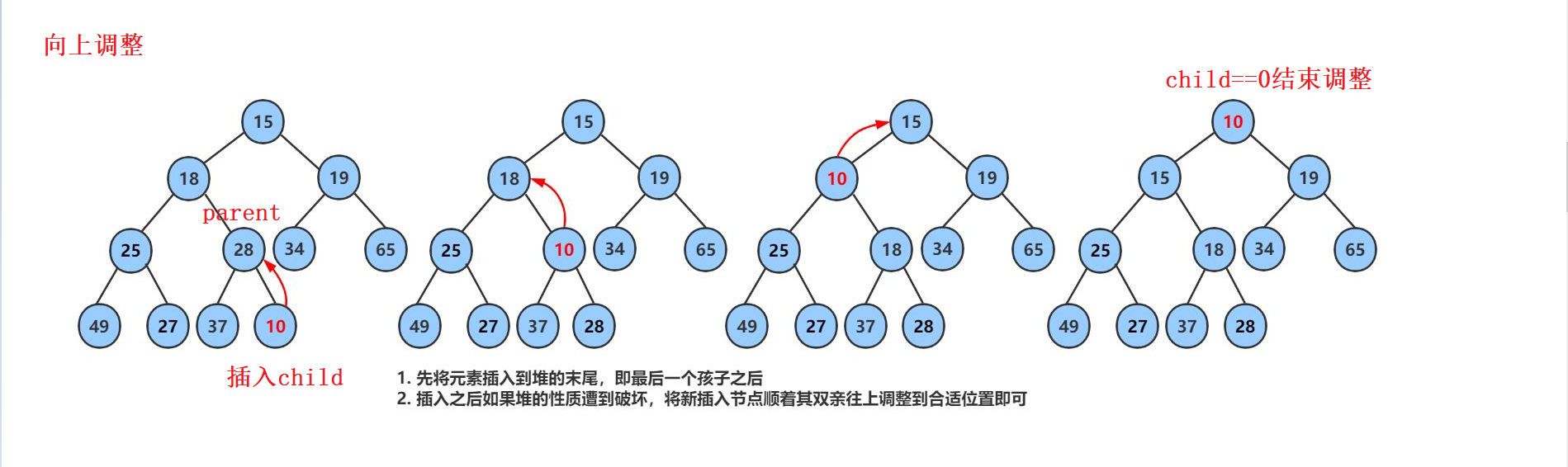
void adjust_up(size_t child)
{
    //仿函数
    Compare com;
	size_t parent = (child - 1) / 2;
	while (child > 0)
    {
        //if ( _con[parent]<_con[child])
		if (com(_con[parent], _con[child]))
        {
            swap(_con[child], _con[parent]);
			child = parent;
			parent = (child - 1) / 2;
        }
        else
        {
            break;
        }
    }
}

3、pop与向下调整

void pop()
{
    swap(_con[0], _con[_con.size() - 1]);
	_con.pop_back();
    adjust_down(0);
}

向下调整：

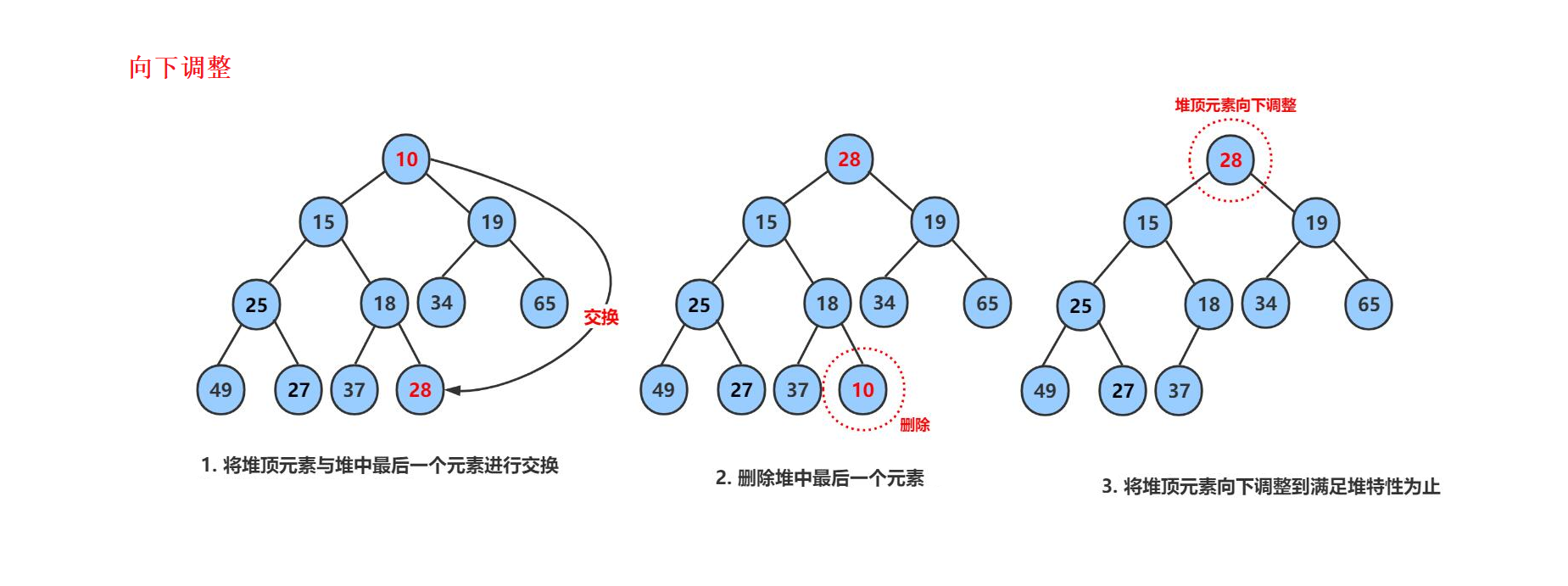
void adjust_down(size_t parent)
{
    Compare com;//仿函数
    size_t child = parent * 2 + 1;
	while (child < _con.size())
    {
        //if (child + 1 < _con.size() && _con[child] < _con[child + 1])
        if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
        {
            child++;
        }
        //if (_con[parent]<_con[child])
        if (com(_con[parent], _con[child]))
        {
            swap(_con[child], _con[parent]);
            parent = child;
            child = parent * 2 + 1;
		}
        else
        {
            break;
		}
	}
}

4、构造函数

这里主要说一下迭代器区间的构造函数：自定义类型会调用自己的迭代器区间构造，所以我们并不需要一个一个push，走个初始化列表即可，同时，数据进去之后我们还要建堆，利用向下调整算法：从倒数第一个非叶子节点，既最后一个节点的父节点开始进行向下调整：

priority_queue()
{}
template <class InputIterator>
priority_queue(InputIterator first, InputIterator last)
    :_con(first, last)
    {
        for (int i = (_con.size() - 1 - 1) / 2; i >= 0; i--)
        {
            adjust_down(i);
        }
    }

5、总体代码

#pragma once
namespace hwc
{
	template <class T>
	class less
	{
	public:
		bool operator()(const T& x, const T& y) const
		{
			return x < y;
		}
	};
	template <class T>
	class greater
	{
	public:
		bool operator()(const T& x, const T& y) const
		{
			return x > y;
		}
	};
	template<class T, class Container = vector<T>, class Compare = less<T>>
	class priority_queue
	{
	public:
		priority_queue()
		{}
		template <class InputIterator>
		priority_queue(InputIterator first, InputIterator last)
			:_con(first, last)
		{
			for (int i = (_con.size() - 1 - 1) / 2; i >= 0; i--)
			{
				adjust_down(i);
			}
		}

		void adjust_up(size_t child)
		{
			Compare com;
			size_t parent = (child - 1) / 2;
			while (child > 0)
			{
				//if ( _con[parent]<_con[child])
				if (com(_con[parent], _con[child]))
				{
					swap(_con[child], _con[parent]);
					child = parent;
					parent = (child - 1) / 2;
				}
				else
				{
					break;
				}
			}
		}

		void adjust_down(size_t parent)
		{
			Compare com;
			size_t child = parent * 2 + 1;
			while (child < _con.size())
			{
				//if (child + 1 < _con.size() && _con[child] < _con[child + 1])
				if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
				{
					child++;
				}
				//if (_con[parent]<_con[child])
				if (com(_con[parent], _con[child]))
				{
					swap(_con[child], _con[parent]);
					parent = child;
					child = parent * 2 + 1;
				}
				else
				{
					break;
				}
			}
		}

		void push(const T& x)
		{
			_con.push_back(x);

			adjust_up(_con.size() - 1);
		}

		void pop()
		{
			swap(_con[0], _con[_con.size() - 1]);
			_con.pop_back();

			adjust_down(0);
		}

		const T& top() const
		{
			return _con[0];
		}

		bool empty() const
		{
			return _con.empty();
		}

		size_t size() const
		{
			return _con.size();
		}
	private:
		Container _con;
	};
}

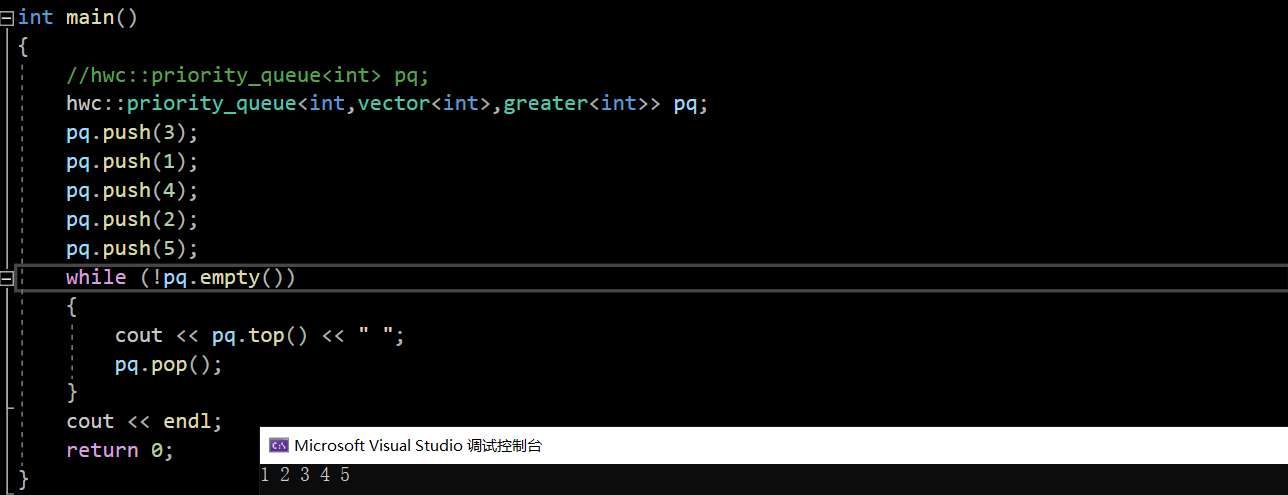
#include <iostream>
#include <queue>
#include <functional>
#include <algorithm>
#include <vector>


using namespace std;

#include "priority_queue.h"


int main()
{
	//hwc::priority_queue<int> pq;
	hwc::priority_queue<int,vector<int>,greater<int>> pq;
	pq.push(3);
	pq.push(1);
	pq.push(4);
	pq.push(2);
	pq.push(5);
	while (!pq.empty())
	{
		cout << pq.top() << " ";
		pq.pop();
	}
	cout << endl;
	return 0;
}