本文首发于馆主君晓的博客,文章链接
简要介绍
这是谷歌和多伦多大学合作的一篇发表在CVPR2022上的工作,延续NeRF重建的相关思路。考虑到之前的一些工作要么是在合成数据集上进行的NeRF重建,要么就是用到真实的场景,但是场景很小,这篇文章主要关注街景的重建和新视图的生成。Urban NeRF主要针对原始NeRF做了三个扩展,扩展如下:
- 增加了输入数据的模态,引入异步捕获的点云数据。
- 解决捕获的图像之间曝光度变化的问题。
- 利用得到的分割mask来监督指向天空的射线上点的体积密度。

方法概览如上图,输入就是多视角的图像以及激光雷达扫描得到的点云,然后渲染出各种新视角的图像以及重建得到的准确的3D结构。至于作者是如何利用点云数据的,如何得到重建的mesh的,我们在后文会讲到。
核心方法
首先是核心方法的整体介绍,损失函数分为两个部分。第一个部分是光度一致性损失,第二部分是点云相关的损失。光度一致性损失就是就是原始NeRF的损失,也就是对应位姿渲染出来的图像与真实图像的MSE损失。这里与原始NeRF有一些区别的地方就在于渲染的时候加入了曝光变量 β \beta β。因为不同的图像在不同的位置拍摄,从而受到的光照是不一样的,所以这个对图像的渲染是存在影响的,所以这里加入了曝光参数,是一种常见的做法。
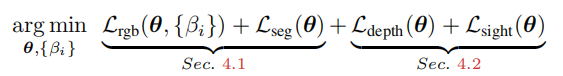
接下来详细介绍一下作者是如何做的。首先是曝光补偿,作者提到我们使用现代化耳朵设备去拍摄照片,通常都是相机设置的自动曝光和自动白平衡。由于相机的自动曝光和自动白平衡,这对NeRF的渲染过程造成很大的困难,因为我们不知道每一张图像的曝光参数这些,而且不同图像的曝光参数不一样。对于这个问题之前有人提到,他们通常引入一个隐码(latent code)来对每一张图像的外观进行编码(appearance code)。使用隐码来对每一张图像的外观进行编码是没有问题的,但是作者认为拍摄出来的照片主要是白平衡和曝光补偿的区别,所以作者认为直接用隐码输入到网络中是一种过度参数化,会解决那些非曝光补偿的错误。作者的观点就是,既然我们认为渲染出来的照片主要与白平衡和曝光补偿相关,那么我们就去解决这个问题。这里作者仍然采用隐码的方式,但不同的是,作者这里是学一个仿射变换(3x3的仿射矩阵),这样就只建模白平衡和曝光补偿。那么其它因素的影响就不会考虑进去了。而且这个仿射变换是直接加在渲染的过程中的。
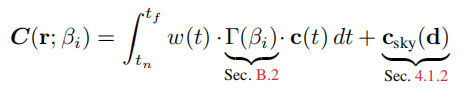
接着便是天空建模。首先这篇文章关注的是街景相关的建模的渲染,那不可避免的,图像中会拍摄到天空。对于天空区域的光线,没有穿透过任何不透明的表面,那么在训练的过程中,对这部分的监督是微弱的。那么作者就考虑天空部分单独进行处理,首先使用分割网络对图像进行分割,分割成有天空区域和没有天空的区域形成mask。对于天空区域的光线,因为没有障碍物遮挡,那么体积密度肯定就是0,那么就会出现下面的损失函数。其中 S i ( r ) S_{i}(r) Si(r)表示某条光线是否是朝向天空的光线,是就是1,否则为0。
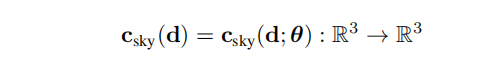
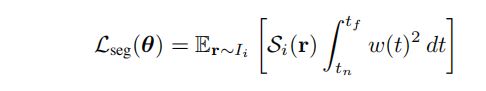
到此为止,光度一致性损失算是讲完了。接下来是lidar相关的损失。首先是深度监督,既然引入了激光雷达扫描得到的点云,那么自然便是深度监督。即渲染得到的深度去匹配雷达点云中的深度。具体损失函数如下:
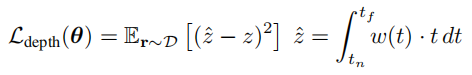
除此之外,还有一个重要的深度损失就是视线先验,对于激光雷达观测到的点,一个合理的假设是,一个测量点p对应于一个非透明表面上的位置,大气介质对激光雷达测量的颜色没有贡献。说人话就是对于某个物体表面上的一点,其颜色与该点附近的体积密度有关,与更远的空气介质无关。那么我们期望辐射集中在沿着射线的一个点上,也就是说一个点负责观察到的颜色,如下面公式所示:
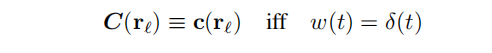
即是当且仅当权重函数等于冲激函数(狄拉克函数),一条射线上所有颜色的集合只等于某一点的颜色。这里解释一下为什么要当权重函数等于狄拉克函数,首先狄拉克函数在定义域内 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)积分为1,也就是面积为1。其次是任意不包含0的区间内积分为0。既然是冲击函数,也就是就在某一点有明显强烈的值,但是在其它点就没有。而我们知道NeRF的权重函数表示从某一点到某一点光线的透射率,如果权重函数为狄拉克函数,那么就表示只在某一点不透,其它点全透。那么就能够表达出作者想要表达的视觉先验了,即从光线原点出发,到达的第一个在物体表面上的点,决定颜色,在那之前和之后的点都不决定这个颜色。于是loss可以变成下面的样子,也就是从 [ t n , t f ] [t_{n},t_{f}] [tn,tf]对权重函数与狄拉克函数的差进行积分,值越小越符合我们的这个先验。
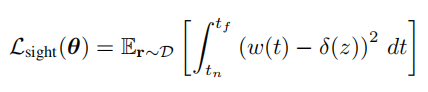
为了让数值更容易处理,作者这里将狄拉克函数换成了一个分布,均值为0,方差为 ( ϵ 3 ) 2 (\frac{\epsilon}{3})^{2} (3ϵ)2,这样的一个分布。除此之外,为了便于计算,作者将这样的一个损失函数分为三个部分,一个是处于射线原点到物体表面点附近的empty loss,另外一个就是物体表面点附近的near loss。最后一个是从物体表面点到最远端点的distant loss。
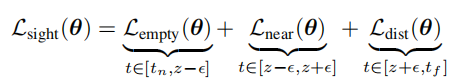
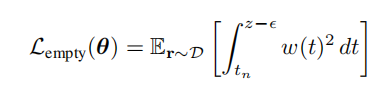
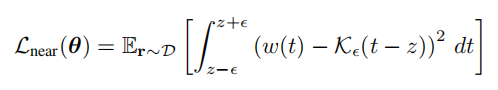
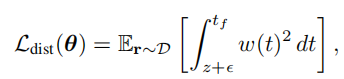
在empty和dist阶段,都是想让他们的权重函数尽量越小越好,因为和他们没有太大关系。在near阶段,则是让权重函数与冲击函数越接近越好。这就是将实现先验用到了损失函数当中,当然作者也提到过,在这里需要控制到 ϵ \epsilon ϵ的大小,太小的 ϵ \epsilon ϵ会影响模型的performance,作者在补充材料中提到使用一种指数衰减策略来找到一个合适 ϵ \epsilon ϵ。
实验相关
首先是数据,作者选取的是街景数据集(Street View Dataset),并且做了两种设置,一种设置是将每个场景分为训练集和测试集,对于测试集是随机选取20%的图像用作测试集。选取所有的与相机位置接近的lidar rays作为我们的测试集。另外一种设置是为了评价作者的模型在没有lidar的情况下会表现出什么样子。所以选取建筑物,将光线终止在建筑物表面的光线全部抹去(不使用),用剩下的lidar rays作为我们的训练集。
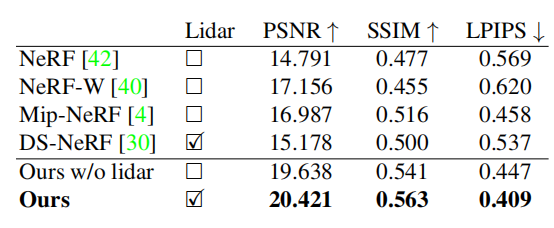
然后就是选取的basline,主要选择了四个模型:NeRF,Mip-NeRF、DS-NeRF、NeRF-W。对于生成新视角图像的这个任务,实验结果对比如下,我们可以看到在PSNR、SSIM、LPIPS这三个指标上,本文提出的方法都达到一个SOTA的结果。不过我认为与选择的场景有关,因为本文是为了街景而设计的NeRF,其它的NeRF除了NeRF-W能够用于室外,其它都是在室内场景下表现不错。
然后是重建相关的指标对比,如下图,就不做过多介绍了。接着是消融实验。

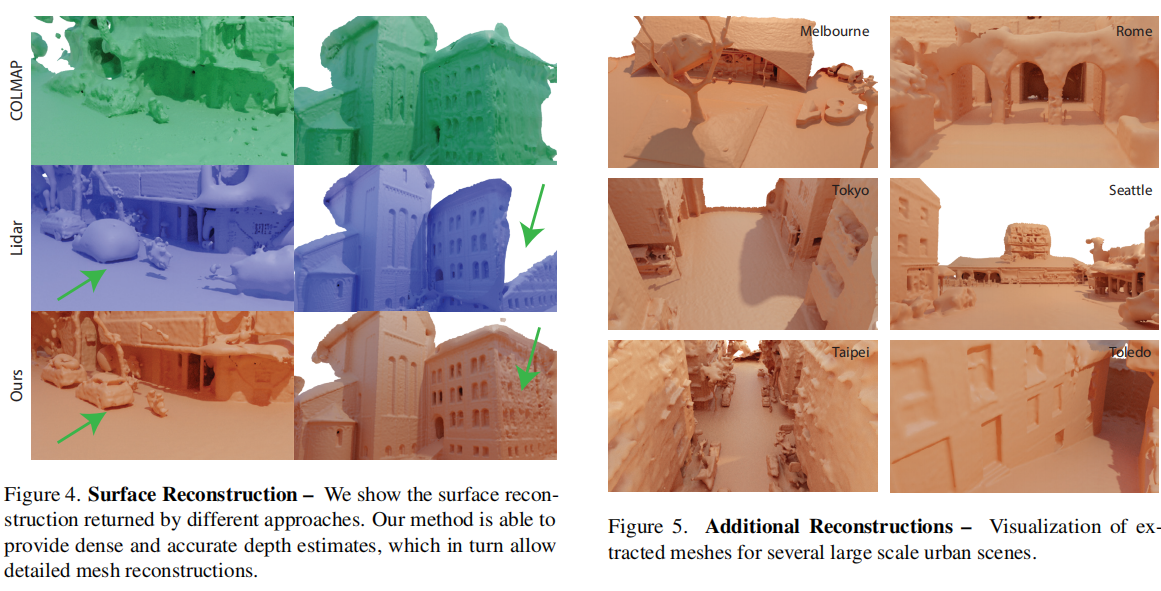

总结
总体来说这篇文章的思路是清楚的,首先确定任务为街景重建,之后找到目前室外的基于NeRF重建存在的几个问题,首先是光照的变化,将latent code解码成仿射变换,直接关注曝光补偿和白平衡。然后是对于天空的那些射线,体积密度的监督。接着便是引入lidar scan做的一些工作,深度监督自然是少不了的。关键的是那个视线先验,确定物体表面上的一点的颜色与该点相关,而与其它点关系不大,从而得到insight loss。不过有点可惜的是这篇文章没有开源代码,也没有非官方的开源代码,不知道是何原因,以后若有时间,复现一下。