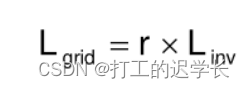1、题目：

A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）-- everyone involved in moving a product from supplier to customer.

Starting from one root supplier, everyone on the chain buys products from one's supplier in a price P and sell or distribute them in a price that is r% higher than P. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.

Now given a supply chain, you are supposed to tell the highest price we can expect from some retailers.

Input Specification:

Each input file contains one test case. For each case, The first line contains three positive numbers: N (≤105), the total number of the members in the supply chain (and hence they are numbered from 0 to N−1); P, the price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then the next line contains N numbers, each number Si​ is the index of the supplier for the i-th member. Sroot​ for the root supplier is defined to be −1. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the highest price we can expect from some retailers, accurate up to 2 decimal places, and the number of retailers that sell at the highest price. There must be one space between the two numbers. It is guaranteed that the price will not exceed 1010.

Sample Input:

9 1.80 1.00
1 5 4 4 -1 4 5 3 6

Sample Output:

1.85 2

2、24分思路：

将该问题看成最长路处理，每条有向边的权重都是1 + r/100，求出最长的那个，并统计有多少条最长路。

有一个点过不去，无语死了

代码如下：

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-8;
int h[N],e[2*N],ne[2*N],idx;
double w[2*N];

double dist[N];
ll cntdist[N];
bool st[N];
int n;
double p,r,maxx=-2e9;
ll cnt = 0;
void add(int a,int b,double c)
{
	e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
}
void spfa(int x)
{
	memset(dist,-0x3f,sizeof dist);
	queue<int> q;
	dist[x] = p;
	cntdist[x] = 1;
	q.push(x);
	while(q.size())
	{
		int t = q.front();
		q.pop();
		for(int i = h[t];~i;i = ne[i])
		{
			int j = e[i];
			if(dist[j] < dist[t] * w[i])
			{
				dist[j] = dist[t] * w[i];
				q.push(j);
				maxx = max(maxx,dist[j]);
				cntdist[j] = cntdist[t];
			}
			else if(abs(dist[j]-dist[t]*w[i])<=eps)
			{
				cntdist[j] += cntdist[t];
			}
		}
	}
}
int main()
{
	std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	memset(h,-1,sizeof h);
	cin>>n>>p>>r;
	int sta = 0;// 初始节点 
	if(n==1)
	{
		cout<<p<<endl;
		return 0;
	}
	for(int i = 0;i<n;i++)
	{
		int supply;
		cin>>supply;
		if(supply!=-1)
			add(supply,i,1.0 + r/100);
		else sta = i;
	}
	spfa(sta);
	for(int i = 0;i<n;i++)
	{
		if(abs(maxx-dist[i])<=eps)
		{
			cnt += cntdist[i];
		}
	}
	cout<<fixed<<setprecision(2)<<maxx-1e-6<<" "<<cnt;
	return 0;
}

3、满分思路

用的是深搜，搜索最长距离，如果有更长，就更新，并把数量置为1，如果相等，数量++。

这个思路不错，我参考其他人的题解的，学到了怎么求深度哈哈哈

 代码如下：

#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
const int N = 1e5 + 10;
int n,maxdepth = 0,maxnum = 0,temp,root;
vector<int> v[N];

void dfs(int index,int depth)
{
	if(v[index].size()==0)// 叶子节点 
	{
		if(maxdepth == depth)
			maxnum++;
		if(maxdepth<depth){
			maxdepth = depth;
			maxnum = 1; 
		}
		return;	
	}
	for(int i = 0;i<v[index].size();i++)
		dfs(v[index][i],depth + 1);
}

int main()
{
	double p,r;
	scanf("%d%lf%lf",&n,&p,&r);
	for(int i = 0;i<n;i++)
	{
		scanf("%d",&temp);
		if(temp==-1)
			root = i;
		else 
			v[temp].push_back(i);
	}
	dfs(root,0);
	printf("%.2lf %d",p*pow(1.0 + r/100,maxdepth),maxnum);
	return 0;
}