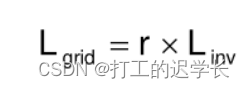一、算法原理

表面法线是几何表面的重要属性，在许多领域（例如计算机图形应用程序）中大量使用，以应用正确的光源来生成阴影和其他视觉效果。

给定一个几何表面，通常很容易将表面上某个点的法线方向推断为垂直于该点表面的向量。但是，由于我们获取的点云数据集代表了真实表面上的一组点样本，因此有两种可能性：

• 从获取的点云数据集中获取底层表面，使用表面网格划分技术，然后从网格计算表面法线；
• 使用近似值直接从点云数据集推断表面法线。

1.理论入门

尽管存在许多不同的法线估计方法，但我们将在本教程中重点介绍的方法是最简单的方法之一，其公式如下。确定表面上一点的法线的问题近似于估计与表面相切的平面的法线的问题，这反过来又变成了最小二乘平面拟合估计问题。

有关更多信息，包括最小二乘问题的数学方程，请参阅pclpy 最小二乘法拟合平面-CSDN博客。

因此，用于估计表面法线的解决方案简化为对从查询点的最近邻居创建的协方差矩阵的特征向量和特征值（或 PCA – 主成分分析）进行分析。更具体地说，对于每个点pi，我们C按如下方式组装协方差矩阵：

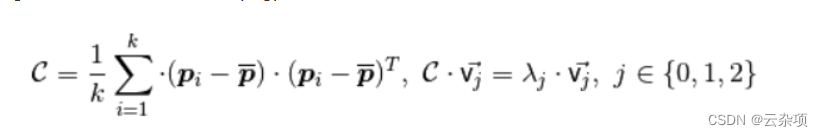
为考虑点邻居的数目在附近 pi，p 表示3D质心最近的邻居，入j是 j)协方差矩阵的特征值第，并且vj 在j个特征向量。

一般来说，因为没有数学方法来求解法线的符号，如上所示通过主成分分析 (PCA) 计算的方向是不明确的，并且在整个点云数据集上的方向不一致。下图展示了这些对代表厨房环境一部分的较大数据集的两个部分的影响。图的右半部分表示扩展高斯图像 (EGI)，也称为法线球体，它描述了点云中所有法线的方向。由于数据集是 2.5D，因此是从单个视点获取的，因此法线应仅出现在 EGI 球体的一半上。然而，由于方向不一致，它们遍布整个球体。

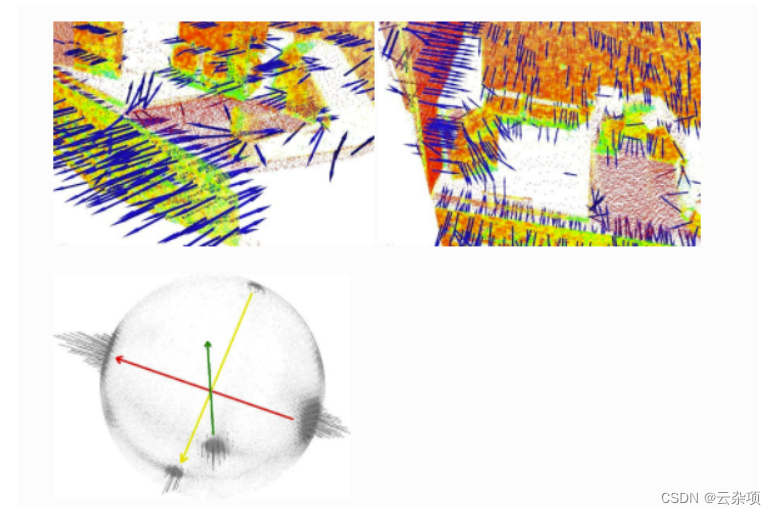
如果观点vp 实际上是已知的，那么这个问题的解决方案是微不足道的。为了使所有法线ni 一致地朝向视点，它们需要满足等式：

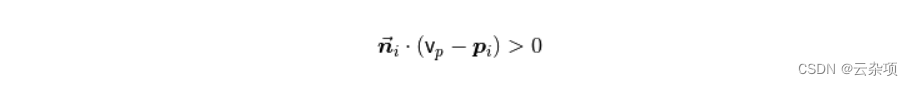
下图显示了上图数据集中的所有法线一致指向视点后的结果。

2.选择正确的比例

如前所述，一个点的表面法线需要从该点的周围点邻域支持（也称为k-neighborhood）估计 。

最近邻估计问题的细节提出了正确比例因子的问题：给定采样点云数据集，正确的k（通过pcl::Feature::setKSearch给出）或r（通过pcl::Feature给出）是多少 ::setRadiusSearch ) 值应该用于确定一个点的最近邻居集？

这个问题非常重要并且构成了点特征表示的自动估计（即，没有用户给定阈值）的限制因素。为了更好地说明这个问题，下图展示了选择较小尺度（即较小的r或k）与较大尺度（即较大的r或k ）的效果）。图中的左侧部分描绘了一个合理的精心选择的比例因子，两个平面的估计表面法线近似垂直，整个桌子上都可以看到小边缘。然而，如果比例因子太大（右侧部分），因此相邻表面的邻居集合更大，覆盖来自相邻表面的点，则估计的点特征表示会失真，在两个平面的边缘处具有旋转的表面法线，并被涂抹边缘和抑制细节。

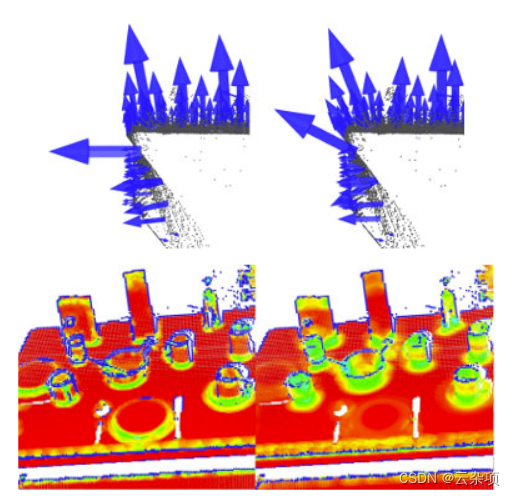
无需涉及太多细节，现在假设必须根据应用程序所需的详细程度来选择确定点邻域的尺度就足够了。简而言之，如果杯子手柄和圆柱部分之间边缘的曲率很重要，则比例因子需要足够小以捕捉这些细节，否则就大。

二、代码

from pclpy import pcl


if __name__ == '__main__':
    # 加载点云
    cloud = pcl.PointCloud.PointXYZ()
    reader = pcl.io.PCDReader()
    reader.read("res/bunny.pcd", cloud)
    print(cloud.size())  # 打印点云的数目
    # 构造法线估计类
    ne = pcl.features.NormalEstimation.PointXYZ_Normal()  # 法线对象
    ne.setInputCloud(cloud)  # 将cloud放入到ne中

    tree = pcl.search.KdTree.PointXYZ()  # 建立kd搜索树
    ne.setSearchMethod(tree)

    cloud_normals = pcl.PointCloud.Normal() 
    ne.setRadiusSearch(0.03)  # 设置半径搜索领域0。03m
    # 计算法线
    ne.compute(cloud_normals)  # 计算法线
    print(cloud_normals.size())  # 打印法线的数目

三、结果

[output]
点云数目： 35947
法线数目： 35947

四、相关数据

法线估计官网：Normal Estimation Using Integral Images — Point Cloud Library 0.0 documentation (pcl.readthedocs.io)