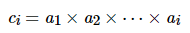今天是打卡第十一天，题目主要是栈结构的运用

20. 有效的括号

题目链接如下：20. 有效的括号

我们挨个遍历字符串，每有一个向左的字符串我们就往栈里面存一个向右的括号，遍历到向右的括号时，如果栈中类型相同就弹出，如果符号条件就是遍历结束且栈中元素为空，否则不符合条件

class Solution {
public:
    bool isValid(string s) {
    stack<char> st;
//如果是奇数，直接剪枝，不可能符合
    if( s.size() % 2 != 0) return false;
    for( int i = 0; i < s.size(); i++){
        if( s[i] == '('){
        st.push(')');
        }else if( s[i] == '{'){
            st.push('}');
        }else if( s[i] == '['){
            st.push(']');
//如果这时为空或者类型不符，则false
        }else if(st.empty() || s[i] != st.top()){
            return false;
        }else{
            st.pop();
        }
        
    }
//看遍历完还有没有剩下的
    return st.empty();
    }
};

1047. 删除字符串中的所有相邻重复项

题目链接如下：1047. 删除字符串中的所有相邻重复项

如果和栈顶存有元素相同，我们删除，反之加入栈中，思路和代码都很容易

class Solution {
public:
    string removeDuplicates(string s) {
    string res;
    for( char x : s ){
//为空为优先条件，证明还没有两个一样的字母
    if(res.empty() || x != res.back()){
        res.push_back(x);
    }else{
        res.pop_back();
    }
    }
    return res;
    }
};

在翻题目评论时看到别人写的原地修改，实在厉害，模拟栈的做法

class Solution {
public:
    string removeDuplicates(string S) {
        int top = 0;
        for (char ch : S) {
            if (top == 0 || S[top - 1] != ch) {
                S[top++] = ch;
            } else {
                top--;
            }
        }
        S.resize(top);
        return S;
    }
};

150. 逆波兰表达式求值

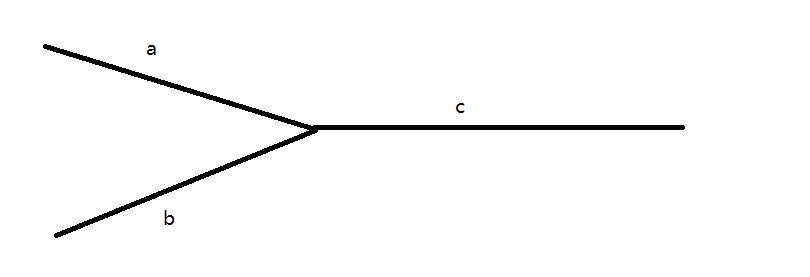
逆波兰表达式的顺序实际上就是二叉树的后序遍历，二叉树节点为运算符号，叶子为数字

以(1+2)*(3*4)为例：

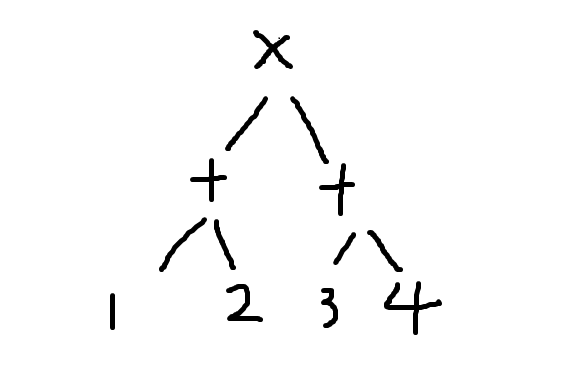
这样做便于计算机运行效率的提高，因为不用在意括号的优先级，虽然有点反人类

题目也说了用栈解决，那我们就用栈解决吧

注意这里是一个string数组，所以每个元素都是字符串，我们要用双引号

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
    stack<int> st;
    for(int i = 0; i < tokens.size(); i++){
        if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
            int num1 = st.top();
            st.pop();
            int num2 = st.top();
            st.pop();
            if (tokens[i] == "+") st.push(num2 + num1);
//注意是num2 - num1
            if (tokens[i] == "-") st.push(num2 - num1);
            if (tokens[i] == "*") st.push(num2 * num1);
            if (tokens[i] == "/") st.push(num2 / num1);
        }else{
//stoi函数是把字符串转换成数字
            st.push(stoi(tokens[i]));
        }
        
    }
//这里不清空栈直接返回也行
    int res = st.top();
        st.pop();
        return res;
    }
};