2022年9月CSP认证题解如此编码（k进制），何以包邮？（背包问题），吉祥物投票（珂朵莉树、懒标记、并查集）

news2025/10/25 14:07:12

在这里插入图片描述

T1 如此编码

思路

由公式
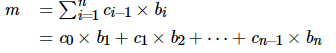
在这里插入图片描述
和前缀乘积定义

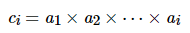
得 $m=b_1+a_1\times b_2+···+a_1\times a_2\times···\times a_{n-1}\times b_n$ ，
上述公式可以提取公共乘项 $a_i$ ，写成 $m=(b_nb_{n-1}···b_1)_{a}$ ，类似 $k$ 进制表达，但每一位权的变化倍数不是常数 $k$ ，而是 $a_k$ ，对于 $b [i]$ 的求解，类比10进制转 $k$ 进制，将 $k$ 替换为 $a [i]$ 即可。

代码

void solve() {
    int n, m;
    cin >> n >> m;
    vector<int> a(n), b(n);
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0; i < n; i++) {
        b[i] = m % a[i];
        m /= a[i];
    }
    for (int i = 0; i < n; i++) cout << b[i] << ' ';
    cout << '\n';
}

T2 何以包邮？

思路

背包问题，问题等价于求 $(m - x)$ 的钱最多买几本书。

代码

void solve() {
    int n, x; 
    cin >> n >> x;
    vector<int> a(n);
    int sum = 0;
    for (int i = 0; i < n; i++) cin >> a[i], sum += a[i];
    int v = sum - x;
    vector<int> dp(v + 1, 0);
    for (int i = 0; i < n; i++) {
        for (int j = v; j >= 0; j--) {
            if (j >= a[i]) {
                dp[j] = max(dp[j], dp[j - a[i]] + a[i]);
            }
        }
    }
    cout << sum - dp[v] << '\n';
}

T4 吉祥物投票

思路

看见区间赋值操作且维护区间长度为 $1 e 9$ ，很容易想到珂朵莉树，用set维护一系列区间。

珂朵莉树模板

结构体node中v用mutable修饰，访问容器set时迭代器const修饰，只读，通过该mutable使得整个结构体只读时该成员仍可变，为后面区间加操作铺垫。
split()将区间从pos处断开，并返回以pos为左端点的迭代器。这里首先调用set自身的二分方法lower_bound()找到左端点不小于pos的区间，找到后判断it->l == pos，若满足则不需要断开区间，直接返回；否则pos在前面一个区间中，将该区间断开为node(L, pos - 1, V)和node(pos, R, V)，重新插入容器，insert方法成功插入后返回迭代器，返回该对象。
assign()区间赋值，这里先split(r+1)获取结束端点是因为(r+1)可能在begin指向区间，操作使迭代器begin失效。之后erase(begin,end)，插入新区间即可。

struct node {
    ll l ,r;
    mutable ll v;
    node(ll l, ll r, ll v) : l(l), r(r), v(v) {}
    bool operator<(const node &a) const { return l < a.l; }
};

set<node> tree;

set<node>::iterator split(ll pos) {
    auto it = tree.lower_bound(node(pos, 0, 0));
    if (it != tree.end() && it->l == pos)
        return it;
    it--;
    ll L = it->l, R = it->r, V = it->v;
    tree.erase(it);
    tree.insert(node(L, pos - 1, V));
    return tree.insert(node(pos, R, V)).first;
}

void assign(ll l, ll r, ll v) {
    auto end = split(r + 1), begin = split(l);
    tree.erase(begin, end);
    tree.insert(node(l, r, v));
}

部分分做法

用一个数组cnt[]维护每个作品的得票，在assign操作时实时更新，这样可以 $O (1)$ 回应操作4，查询每个作品的得票。
对于操作2,3，暴力 $O (m)$ 访问容器内所有段，修改v值，由于mutable关键字我们可以直接通过迭代器修改。
对于操作5，开一个map，暴力 $O (m)$ 访问容器内所有段，统计最大者。
这样可以得45分。

全部分做法

① 首先，用set维护区间最大值， $O (1)$ 回应操作5，这个在之前的3月份的第四题通信管理中也用到过，详见我的博客CSP22.3 T4通信系统管理；
② 对于操作2,3，我们并不需要真的修改容器内的值，只需要改变标签和v值的映射即可，一种懒惰更新方法，开一数组lazy[]，标签 $i$ 所对应的v值为lazy[i]，对于操作2，交换lazy[x]和lazy[y]；而对于操作2，我们引入并查集，将多个v值映射到一个懒标记lazy[w]上，此时标签 $i$ 所对应的v值可能有多个，满足find(v)=lazy[i]，同时lazy[x]赋一个从未使用过的数字即可，另外我们维护从懒标记到标签的映射inv[]。

举个例子：
假设set中维护了以下段：（1，3，2），（4，5，1），（6，9，3），（10，12，2），此时还未执行过操作2,3，标签和lazy，fa层之间的映射为

tag	lazy	fa
1	1	1
2	2	2
3	3	3

执行操作3 1 2后，容器内容不变：

tag	lazy	fa
1	2	1
2	1	2
3	3	3

这时统计标签为1的段，应该统计val值满足lazy[1]=2的段，执行操作2 2 1之后，容器同样不变，而映射变为：

tag	lazy	fa
1	2	2
2	4	2
3	3	3
		4

统计标签为1的段，应统计val值满足find(val)=lazy[1]=2的段，即val值为1,2的段。

坑

有一个地方我调了很久，就是操作5中输出最多得票的编号最小者，这个编号经过层层映射，早已不是容器内v值，或者find(v)，而是对应标签inv[find(v)]的最小者，由于我们插入时已经取了find(v)，保证v==find(v)，因此将所有最多得票者的inv[v]中取最小输出答案。

代码

struct node {
    int l ,r;
    mutable int v;
    node(int l, int r, int v) : l(l), r(r), v(v) {}
    bool operator < (const node &a) const { return l < a.l; }
};

struct pp
{
    int k, v;
    bool operator < (const pp& a) const {
        if (v != a.v) return v > a.v;
        return k < a.k;
    }
};

set<node> tree;     // Chthollty tree
int lazy[200005], cnt[200005], fa[200005];
map<int , int> inv;     // 建立标记和标签之间双射
set<pp> all;  // 维护区间最值

int _find(int x) {
    if (x == fa[x]) return x;
    return (fa[x] = _find(fa[x]));
}

void _union(int x, int y) {
    fa[_find(y)] = _find(x);
}

set<node>::iterator split(int pos) {
    auto it = tree.lower_bound(node(pos, 0, 0));
    if (it != tree.end() && it->l == pos)
        return it;
    it--;
    int L = it->l, R = it->r, V = it->v;
    tree.erase(it);
    tree.insert(node(L, pos - 1, V));
    return tree.insert(node(pos, R, V)).first;
}

void assign(int l, int r, int v) {
    auto end = split(r + 1), begin = split(l);
    int tv; // 标记可能被操作2合并至另一个标记，fa[]存储真实标记
    for (auto it = begin; it != end; it++) {
        tv = _find(it->v);
        all.erase({tv, cnt[tv]});
        cnt[tv] -= (it->r - it->l + 1);
        all.insert({tv, cnt[tv]});
    }
    tree.erase(begin, end);
    tv = _find(v);
    tree.insert(node(l, r, tv));
    all.erase({tv, cnt[tv]});
    cnt[tv] += (r - l + 1);
    all.insert({tv, cnt[tv]});
}

void solve() {
    int n, m, q; cin >> n >> m >> q;
    int tot = m;
    tree.insert(node(1, n, 0));
    for (int i = 0; i <= max(2 * m, 2 * q); i++) lazy[i] = fa[i] = i;
    for (int i = 1; i <= m; i++) inv[i] = i;

    cnt[0] = n;
    all.insert({0, n}); // 1e9

    int op, l, r, x, w, y;
    while (q--) {
        cin >> op;
        if (op == 1) {
            cin >> l >> r >> x;
            assign(l, r, lazy[x]);
        }
        else if (op == 2) {
            cin >> x >> w;
            int fx = lazy[x], fy = lazy[w];
            all.erase({fx, cnt[fx]});
            all.erase({fy, cnt[fy]});
            cnt[fy] += cnt[fx];   // 标记lazy[x]弃用
            all.insert({fy, cnt[fy]});
            _union(fy, fx);
            lazy[x] = ++tot, inv[tot] = x;  // 创建一个新标记
        }
        else if (op == 3) {
            cin >> x >> y;
            swap(inv[lazy[x]], inv[lazy[y]]);
            swap(lazy[x], lazy[y]);
        }
        else if (op == 4) {
            cin >> w;
            cout << cnt[lazy[w]] << '\n';
        }
        else if (op == 5) {
            int ans = 0, ansi = 0;
            for (auto it : all) {
                if (it.k && it.v > ans) {
                    ans = it.v;
                    ansi = inv[it.k];
                }
                if (it.k && it.v == ans && inv[it.k] < ansi) ansi = inv[it.k];
                if (ans > it.v) break;
            }
            cout << ansi << '\n';
        }
    }
}