求非线性方程或方程组解的问题也就是求函数零点的问题。对于任意函数,在求解范围内可能有零点,也可能没有;可能只有一个零点,也可能有多个甚至无数个零点。MATLAB没有可以求解所有函数零点的通用命令,下面将分别讨论一元函数和多元函数零点的求解问题。
一元函数的零点
在所有函数中,一元函数是最简单的。在MATLAB中,可以使用fzero 函数来计算一元函数的零点,具体调用方法如下。
x =fzero( fun, x0) %在x0点附近寻找函数fun的零点
x =fzero( fun , x0 , options) %options为使用optimsect 函数设定优化器参数的选项
x =fzero( fun ,[ x0,x1]) %在[ x0,x1]区间寻找函数fun的零点
optimset 函数的具体调用方法如下。
optimset%显示优化器的现有参数名及其参数值
options = optimset( " paraml',value1 ,' param2 ' ,value2,...)%使用参数名和参数值设定优化器的参数
options = optimset( oldopts, ' paraml ' ,value1,...)%在现有优化器oldopts的基础上,使用参数名和参数值变更优化器参数
optimset 函数中可以设置的主要优化器参数见表。
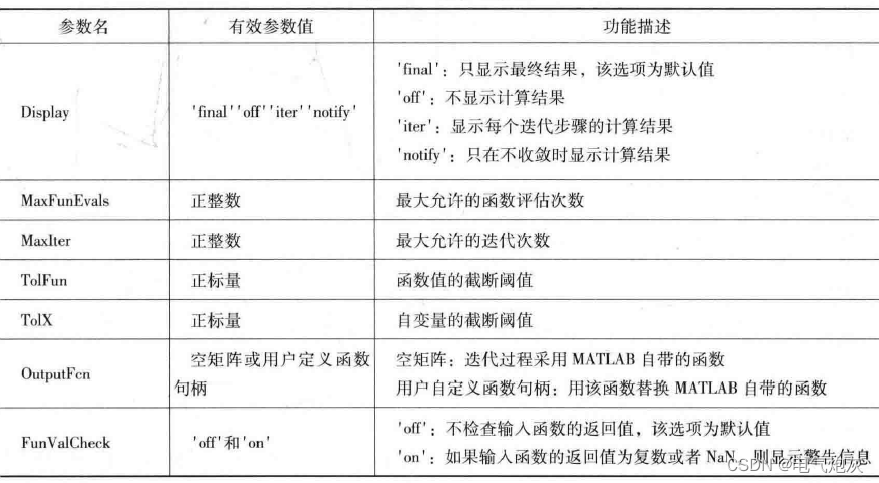
例:计算一元函数fx )= (x^2)*cosx一x+1在[-3,3]区间上的零点。
首先绘制函数的曲线,在命令行窗口中输入如下语句。
>>x=-3:0.1:3;
y =x.*x.*cos( x)-x+1;
plot(x,y,'r ')
xlabel( 'x ');ylabel('fx)');
title( 'The zero of function ')
hold on
h=line([-3,3],[0,0]);
set( h, 'color '.'g')
grid;
图形窗口中的输出结果如图所示。
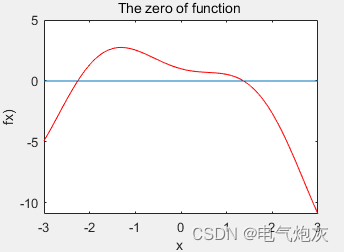
在求解函数零点之前,先绘制函数的图形,这样在后面的步骤中使用fzero命令时,方便选择初始数值x0。由上图不难看出,曲线在[ -3,3]区间内包含2个零点。
计算函数在某点附近的零点,在命令窗口中输入如下语句。
>>f=@(x)x*x * cos(x)-x+1;
X1 =fzero(f,-2)
X2=fzero(f,1)
命令行窗口中的输出结果如下所示。
X1=
-2.2621
X2=
1.3719
多元函数的零点
非线性方程组的标准形式为F(x)=0,其中x为向量,F(x)为函数向量。在MATLAB中,使用fsolve命令求解多元函数,具体调用方法如下。
X=fsolve( fun,xo) %在向量x附近寻找函数fun的解
X=fsolve( fun,xo , options) %使用options设定优化器参数
例:求解二元方程组的零点。
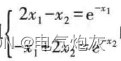
首先绘制函数的曲线,在命令行窗口中输人如下语句。
>>x=[-5:0.1:5];
y=x;
[X,Y] = meshgrid(x,y);
Z=2*X-Y-exp( -X);
surf(X,Y,Z)
xlabel( 'x ')
ylabel( 'y')
zlabel('z ')
title( 'The figure of the function ')
图形窗口中的输出结果如图所示。
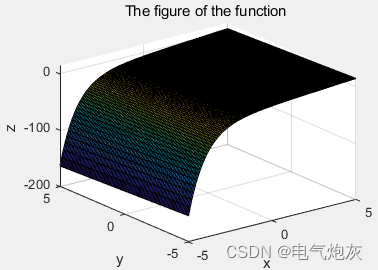
编写对非线性方程组进行函数描述的M文件,输人代码如下。
function F= fsolvefun(x)
F=[2*x(1)-x(2)-exp(-x(1));-x(1)+2*x(2)-exp( -x(2))];
将上述程序代码保存为fsolvefun. m文件。
下面求解二元函数的零点,在命令行窗口中输人如下语句。
>>x0=[-5;-5];
options =optimset( 'Display ','iter ');
x= fsolve( @ fsolvefun, x0 ,options)
命令行窗口中的输出结果如下所示。
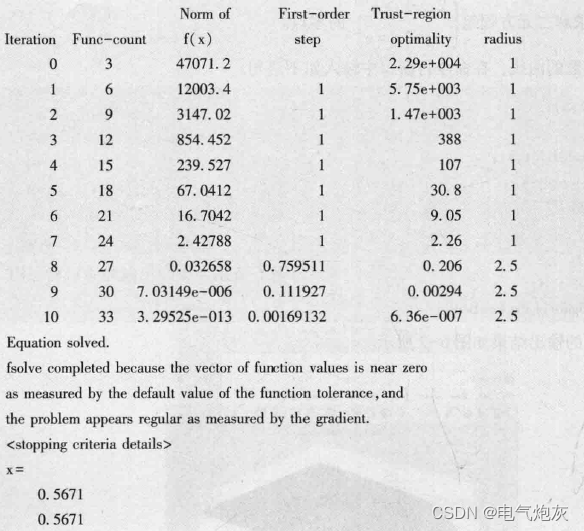
例:求解

编写对非线性方程组进行函数描述的M文件,并保存为myfun6. _8. m,如下所示。
function T= myfun6_ 8(x)
T=x^4-[2,5;-8,7];
然后求解非线性方程组,在命令行窗口中输人如下语句。
>>x0=[3 1;2 1];
options= optimset( 'Display',' of');
X= fsolve( @ myfun6 8, x0 options)
命令行窗口中的输出结果如下所示。
X=
1.4438 0.3202
-0. 5123 1.7640