LeetCode59:

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

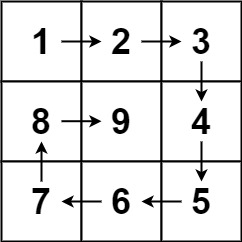
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：1 <= n <= 20

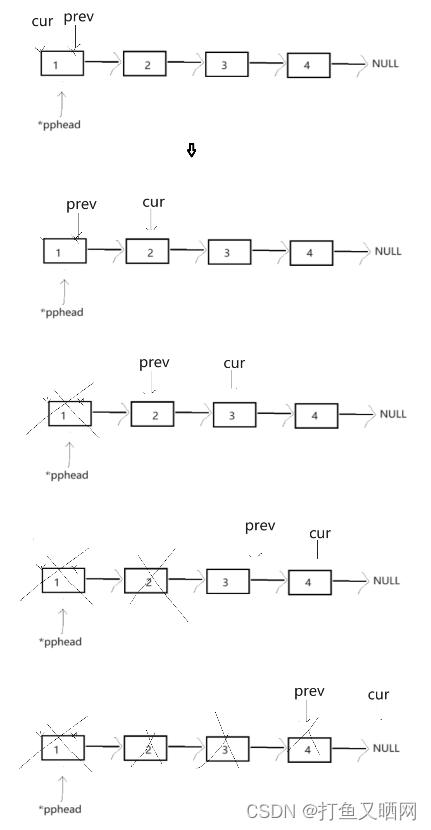
思路分析： 这道题目不考具体的算法，纯模拟过程，考察对边界条件的处理和对代码的掌控能力。

模拟顺时针画矩阵的过程：

1.填充上行从左到右

2.填充右列从上到下

3.填充下行从右到左

4.填充左列从下到上

由外向内这样一圈一圈画下去，画每一条边都必须坚持左闭右开原则。

代码:

class Solution:
    def generateMatrix(self, n: int)-> List[List[int]]:
        nums = [[0] * n for _ in range(n)]  # 创建一个长度为n，值均为0的列表
        startx, starty = 0, 0  # 起始点为[0,0]
        loop, mid = n // 2, n // 2  # 整除2，设置循环的层数（往里缩一圈需要减少2个位置）、n为奇数时； 矩阵的中心点
        count = 1  # 计数

        for offset in range(1, loop + 1):  # 每循环一层偏移量加1， 偏移量从1开始

            for i  in range(starty, n - offset):  # 设置上行，从左至右，左闭右开
                nums[startx][i] = count  # 行标不变，列标递增
                count += 1  # 计数递增

            for i in range(startx, n - offset):  # 设置右列，从上至下，左闭右开
                nums[i][n - offset] = count  # 列标不变，行标递增
                count += 1 # 计数递增

            for i in range(n - offset, starty, -1):  # 设置下行，从右至左，左闭右开
                nums[n - offset][i] = count  # 行标不变（下行行标为n-offset，动态变化)，列标递增
                count += 1 # 计数递增
            
            for i in range(n - offset, startx, -1):  # 设置左列，从下至上，左闭右开
                nums[i][starty] = count  # 列坐标是starty, 而不是n-offset哦！
                count += 1 # 计数器递增
            
            startx += 1
            starty += 1  # 注意循环完一圈后，startx, starty都要加1哦
        
        if n % 2 != 0:  # 当n为奇数时，填充中心点
            nums[mid][mid] = count  # 因为上面每次赋值完，count都会后加1，所以直接赋值就好了
        return nums  # 返回排列好的矩阵
                


        

总结：处理边界需要严格按照左闭右开的原则，另外理解loop怎么算也很关键。上述代码的注释写的非常详细，复习时应精读来理解整个过程。