线性回归
什么是线性回归
1 线性回归是一个有监督算法。简单来说在有监督模型中有两种问题,第一种是分类问题,一种是回归问题
2 分类问题就是会有几个类别,不是1就是0。(去银行贷款,是否给贷款就是分类,1就是给,0就是不给)
3 回归问题就在一定范围内找出一个确定的值。(去银行贷款,问可以贷款多少,得出的数字就是解决一个回归问题)
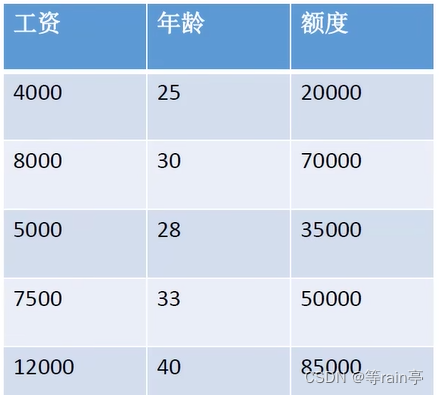
对于上图,由于工资和年龄都会对额度产生影响。设工资和年龄分别为x1和x2,额度是Y。我们希望得到x1和x2的系数对于Y的影响。建立αx1+βx2=Y回归方程,希望通过Y,x1,x2得到α和β,这个就是我们线性回归的一个核心目标。

现在我们从 αx1+βx2=Y 回归方程知道这个是一种线性的回归方程,那既然是线性回归方程就没有办法满足现实中可能出现的一些特殊的产生波动的点,类似与上图。图中红色的点就是通过x1和x2得到的Y,图中的平面是回归方程算出的Y。因为由于线性方程的问题,没有办法去涵盖所有的Y值,所以希望得到的回归方程可以尽可能的满 足更多的Y。
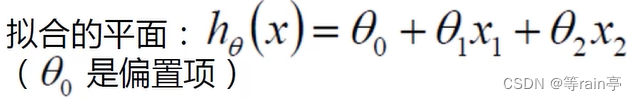
公式中相对于αx1+βx2=Y 多出了一个 。这个参数就是为了调节算出的结果可能与真实的结果不相同而添加的偏置项,
1和
2可以看成x1和x2在这个函数中的权重。
由于此方程有一个单独的,我们希望函数可以写成矩阵的方式进行计算,往往会添加多一个x3与单独的
相乘,那由于公式中独立加了一个单独的
,其实x3的矩阵那一列可以写成全为1,使得
,x3相乘得到的结果还是为
。整合得到下列公式。
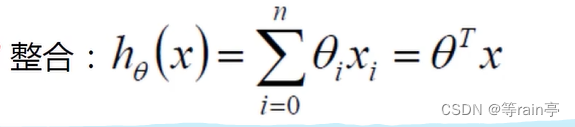
误差

其中 y(i)是真实值,tx(i)是预测值,预测值和真实值之间往往会有差距,所以在公式中加入了
(i),此项为误差项。不同样本的误差项是不相同的,希望误差项接近0。

独立:指的是公式中的i都是相互独立的(去银行贷款,张三李四去贷款是相互独立的)
相同分布:都是算一个结果(都是在这家银行贷款)
服从均值为0的方差为平方的的高斯分布:如下图
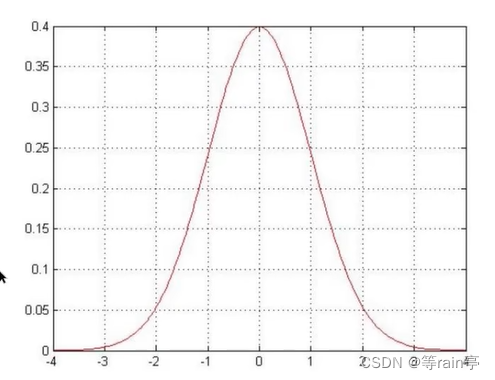
在横轴均值为0的情况下结果是最多的,因为正常情况都是这个范围,而特殊情况可能就比较偏离对称轴。
以上算是笔记,还有很多更深层次的问题可见视频:
1-线性回归整体模块概述_哔哩哔哩_bilibili