🏆个人主页:企鹅不叫的博客
🌈专栏
- C语言初阶和进阶
- C项目
- Leetcode刷题
- 初阶数据结构与算法
- C++初阶和进阶
- 《深入理解计算机操作系统》
- 《高质量C/C++编程》
- Linux
⭐️ 博主码云gitee链接:代码仓库地址
⚡若有帮助可以【关注+点赞+收藏】,大家一起进步!
💙系列文章💙
【C++高阶数据结构】并查集
【C++高阶数据结构】图
【C++高阶数据结构】LRU
【C++高阶数据结构】B树、B+树、B*树
文章目录
- 💙系列文章💙
- 💎一、概念
- 💎二、实现
- 💎三、性能分析
💎一、概念
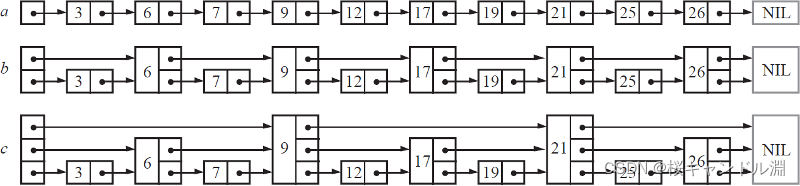
假如我们每相邻两个节点升高一层,增加一个指针,让指针指向下下个节点,如下图b所示。这样所有新增加的指针连成了一个新的链表,但它包含的节点个数只有原来的一半。由于新增加的指针,我们不再需要与链表中每个节点逐个进行比较了,需要比较的节点数大概只有原来的一半。
以此类推,我们可以在第二层新产生的链表上,继续为每相邻的两个节点升高一层,增加一个指针,从而产生第三层链表。如下图c,这样搜索效率就进一步提高了。
实际上,按照上面生成链表的方式,上面每一层链表的节点个数,是下面一层的节点个数的一半,这样查找过程就非常类似二分查找,使得查找的时间复杂度可以降低到O(log n)。
不再严格要求对应比例关系,而是插入一个节点的时候随机出一个层数
一个结点到底应该给几层?
一个节点的平均层数(也即包含的平均指针数目),计算如下:
当p=1/2时,每个节点所包含的平均指针数目为2;
当p=1/4时,每个节点所包含的平均指针数目为1.33。
💎二、实现
设计跳表
思路:
- 首先设计节点,包含节点值和存储next指针
- 跳表设计,定义一个头节点,最大层数,生成层数概率
struct SkiplistNode { int _val; //用来存next指针的vector vector<SkiplistNode*> _nextV; SkiplistNode(int val,int level) :_val(val) ,_nextV(level,nullptr) {} }; class Skiplist { typedef SkiplistNode Node; public: Skiplist() { srand(time(0)); //头结点,层数是1 _head=new Node(-1,1); } vector<Node*> FindPrevNode(int num) { //创建一个临时节点先指向我们的头节点 Node* cur = _head; //初始化我们的层数是我们头结点的层数 int level = _head->_nextV.size() - 1; // 插入位置每一层前一个节点指针 vector<Node*> prevV(level + 1, _head); //当我们还没有走到最底下那一层的时候 while (level >= 0) { // 目标值比下一个节点值要大,向右走 // 下一个节点是空(尾),目标值比下一个节点值要小,向下走 if (cur->_nextV[level] && cur->_nextV[level]->_val < num) { // 向右走 cur = cur->_nextV[level]; } //如果当前层没有下一个节点了 //或者当前层的下一个节点比我们的目标值小 else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num) { //只有当需要转移到下一层的时候,我们才找到了当前层的前置结点 // 更新level层前一个 prevV[level] = cur; // 向下走 --level; } } return prevV; } //查找数据 bool search(int target) { Node* cur=_head; //往最高层走 int level=_head->_nextV.size()-1; while(level>=0) { //目标值比下一个结点值要大,向右走 //下一个节点是空(尾),目标值比下一个结点值要小,向下走 if(cur->_nextV[level]&&cur->_nextV[level]->_val<target) { //向右走 cur=cur->_nextV[level]; } else if(cur->_nextV[level]==nullptr || cur->_nextV[level]->_val>target) { //向下走 --level; }else{ return true; } } return false; } void add(int num) { vector<Node*> prev=FindPrevNode(num); //产生新节点的层数 int n=RandomLevel(); //数据是num,有n层的结点 Node* newnode=new Node(num,n); //如果n超过了当前最大的层数,那就升高一下head的层数 if(n>_head->_nextV.size()) { //将头结点的next数组的大小开辟到我们当前的最大的层数大小,新的部分用nullptr填补 _head->_nextV.resize(n,nullptr); //将我们的前置结点也同样开辟到n的大小 prev.resize(n,_head); } //链接前后节点 //每一层我们都是要更新的 for(size_t i=0;i<n;++i) { newnode->_nextV[i]=prev[i]->_nextV[i]; prev[i]->_nextV[i]=newnode; } } bool erase(int num) { vector<Node*> prev=FindPrevNode(num); //第一层下一个不是val,或者val不在表中 if (prev[0]->_nextV[0]==nullptr ||prev[0]->_nextV[0]->_val!=num) { return false; } else{ Node* del =prev[0]->_nextV[0]; //del结点每一层的前后指针链接起来 for(size_t i=0;i<del->_nextV.size();i++) { prev[i]->_nextV[i]=del->_nextV[i]; } delete del; // 如果删除最高层节点,把头节点的层数也降一下 int i = _head->_nextV.size() - 1; while (i >= 0) { if (_head->_nextV[i] == nullptr) --i; else break; } _head->_nextV.resize(i + 1); return true; } } int RandomLevel() { size_t level=1; // rand()最大值在[0,RAND_MAX]之间 //相当于[0, 1]的范围 while(rand()<RAND_MAX*_p&&level<_maxLevel) { ++level; } return level; } private: Node* _head;//头结点 size_t _maxLevel=32;//最大层数 double _p=0.5;//创建新层的概率 }; /** * Your Skiplist object will be instantiated and called as such: * Skiplist* obj = new Skiplist(); * bool param_1 = obj->search(target); * obj->add(num); * bool param_3 = obj->erase(num); */
💎三、性能分析
- skiplist相比平衡搜索树(AVL树和红黑树)对比,都可以做到遍历数据有序,时间复杂度也差不多。skiplist的优势是:a、skiplist实现简单,容易控制。平衡树增删查改遍历都更复杂。b、skiplist的额外空间消耗更低。平衡树节点存储每个值有三叉链,平衡因子/颜色等消耗。skiplist中p=1/2时,每个节点所包含的平均指针数目为2;skiplist中p=1/4时,每个节点所包含的平均指针数目为1.33;
- skiplist相比哈希表而言,就没有那么大的优势了。相比而言a、哈希表平均时间复杂度是O(1),比skiplist快。b、哈希表空间消耗略多一点。skiplist优势如下:a、遍历数据有序b、skiplist空间消耗略小一点,哈希表存在链接指针和表空间消耗。c、哈希表扩容有性能损耗。d、哈希表再极端场景下哈希冲突高,效率下降厉害,需要红黑树补足接力