本文编辑：调皮哥的小助理

FMCW毫米波雷达系统的性能参数主要包含：

(1)距离估计、距离分辨率、距离精度、最大探测距离;

(2)速度估计、速度分辨率、速度精度、最大不模糊速度；

(3)角度估计、角度分辨率、角度精度、最大角度范围。

分析以及理解上述这些参数有助于我们学习雷达和设计雷达。

一、距离维度

1.距离估计

对中频信号进行 ADC 采样， 然后做 FFT 提取信号的频率信息， 假设 FFT 得到频谱的谱峰值对应的频率为fm ， 则目标的距离信息可以表示如下：

$R=\frac{cT{f}_m}{2B}$

该公式的推导过程已经在之前进行过详细的论述，如果还有不清楚的可以查看下列文章：https://zhuanlan.zhihu.com/p/422798513

2.距离分辨率

距离分辨率表示距离上分辨两个目标的能力，用如下公式表示：

$\Delta R=\frac{c}{2B}$

该公式的推导过程也在之前的文章中详细论述过：https://zhuanlan.zhihu.com/p/510398532,

3.距离精度

测距精度表示测量单目标的距离测量精度，由信噪比和有效带宽决定，用如下公式表示：

${\sigma }_R=\frac{c}{3.6B\sqrt{2SNR}}$

这里的信噪比是距离FFT的信噪比，如果我们带入距离分辨率ΔR，那么上述公式可以写为：

${\sigma }_R=\frac{\Delta R}{1.8\sqrt{2SNR}}$

这样我们也可以说距离精度与距离分辨率和信噪比有关，距离分辨率越小，距离精度值也越小，信噪比越高，距离精度值越小。

关于测距精度的公式推导可以见这两篇论文：
(1)https://ieeexplore.ieee.org/stamp/stamp.jsp?
(2)https://www.mers.byu.edu

4.最大探测距离

雷达最大探测距离，也可以叫做雷达威力。雷达的最大探测距离通常采用基于弗里斯方程的雷达方程来计算，这部分工作通常也叫做雷达链路预算，FMCW雷达的雷达方程如下所示：

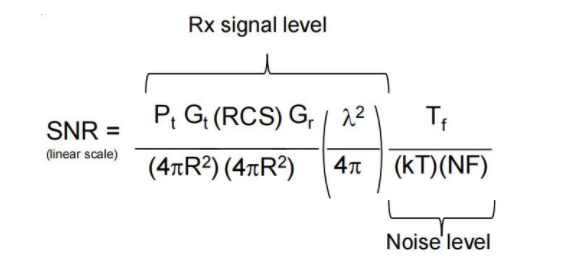
其中，Tf是一帧内Chirp的总时间，如果帧占空比为100%，则Tf等于帧周期，否则Tf般要小于帧周期。Pt是发射功率，Gt是发射天线增益，Gr是接收天线增益。

雷达的最大探测距离还有另外一种计算方法，我习惯称雷达方程为雷达探测距离的决定式，因为只有满足雷达方程，后续的计算和处理才有意义。这种方式的雷达最大探测距离取决于最大的中频信号带宽IFmax，表示如下：

$I{F}_{\max }=S\ast \tau =\frac{2S\ast R_{\max }}{c}$

$R_{\max }=\frac{c\ast I{F}_{\max }}{2S}$

其中，S是调频斜率。最大中频信号的带宽大小与ADC采样率相关，在TI毫米波雷达DCA1000数据采集平台上具备两种模式，如下所示：

(1)在complex 1x模式下:

$I{F}_{\max }\le 0.9\ast f_s$

(2)在complex 2x和实采样模式下:

$I{F}_{\max }\le \frac{0.9\ast f_s}{2}$

因此，也可以用下式来估计最大作用距离，意味着雷达最大探测距离取决于中频信号的采样率：

$R_{\max }=\frac{f_s\ast c}{2S}$

我们也可以采用下面的过程来证明这个实事，也就是说ADC的采样率应该尽可能高，这样对于提升雷达的性能有帮助。

$\min \left\{\frac{\Delta R}{R_{\max }}\right\}=\min \left\{\frac{c}{2B}\ast \frac{2S}{f_s{\ast }_c}\right\}=\min \left\{\frac{1}{f_s\ast T_c}\right\}$

二、速度维度

1.速度估计

雷达速度估计的公式如下所示：

$v=\frac{\lambda \Delta \varphi }{4\pi T_{\mathrm{c}}}$

具体的推导过程见文章：https://zhuanlan.zhihu.com/p/422798513

2.速度分辨率

速度分辨率表示速度维区分两个同一位置的目标的能力。假设一帧传输 N 个Chirp，速度维频率分辨率为：

$\Delta v=\frac{\lambda }{2N{T}_c}$

3.速度精度

测速精度表示测量单目标的速度测量精度，取决于信噪比，同样也可以和上述距离精度分析那样带入速度分辨率公式，该过程读者可以自行推导。

${\sigma }_v=\frac{\lambda }{3.6N{T}_c\sqrt{SNR}}$

4.最大不模糊速度

目标速度是通过提取chirp之间的相位差（多普勒频率）来计算。连续chirp之间的相位差的相位差可表示为：

$\Delta \varphi =2\pi f_c\Delta \tau =2\pi f_c\frac{2\Delta R}{c}=2\pi f_c\frac{2v{T}_c}{c}=\frac{4\pi v{T}_c}{\lambda }$

当相位测量不模糊时：

$|\Delta \varphi |<\pi$

带入上述公式，得到最大不模糊速度为：

$v_{\max }=\frac{\lambda }{4T_c}$

三、角度维度

1.角度估计

相邻天线的波程差 取决于到达角 ：

$\Delta =d\sin (\theta )$

波程差导致相邻天线之间的相位变化 ：

$W=\frac{2\pi }{\lambda }d\sin (\theta )$

该相位变化可以使用三维FFT估计，一旦 被估计，到达角 就可以很容易地求出：

${\theta }_{\mathrm{est}}={\sin }^{-1}\left(\frac{w_{est}\lambda }{2\pi d}\right)$

2.角度分辨率

角度分辨率表示在角度维分离相同距离、速度目标的能力。雷达的角度分辨率一般较低，TI单芯片毫米波雷达AWR1xxx系列1T4R的角度分辨率28°左右。在实际情况下，由于距离、速度分辨率较高，目标一般可以在距离和速度维区分开。

假设接收天线个数为NRx，角度维频率分辨率为:

$\Delta \theta =\frac{2\pi }{N_{RX}}$

$\Delta \omega =\frac{2\pi d}{\lambda }[\sin (\theta +\Delta \theta )-\sin \theta ]=\frac{2\pi d}{\lambda }\cos \theta \Delta \theta >\frac{2\pi }{N_{RX}}$

$\Delta \theta =\frac{\lambda }{N_{RX}d\cos \theta }$

由上述公式可知，角度分辨率随着目标偏离法线的角度增大而增大，在法线位置目标的角度分辨率值最小。

3.角度精度

测角精度表示测量单目标的角度测量精度，取决于信噪比和3dB波束宽度：

${\sigma }_{\theta }=\frac{{\theta }_{3dB}}{1.6\sqrt{2SNR}}$

4.最大探测角度

角度通过RX天线间的接收信号相位差（由波程差引起）来计算，相位差为：

$\omega =\frac{2\pi d\sin \theta }{\lambda }$

当相位差不模糊时，即：

$|\omega |<\pi$

得到测角范围为：

${\theta }_{\max }={\sin }^{-1}\left(\frac{\lambda }{2d}\right)$

上述公式计算可能会得到±90°，但是在实际工程中，角度探测范围还跟天线的波束宽度有关系，一般选择-3dB或者-6dB，所以水平角度范围一般是120°~160°。