大纲
- 1.1统计学习的特点
- 1.2统计学习方法步骤
- 1.3 统计学习的分类
- 基本分类:
- 1.4 监督学习方法的三要素
- 模型:条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)或决策分布 Y = f ( X ) Y=f(X) Y=f(X)
- 策略:在所有假设空间中选择一个最优模型
- 注意事项:
- 算法:学习模型的具体计算方法
- 1.5 训练误差与测试误差
- 1.6过拟合与模型选择
- image-20230106222807847
- 在多项式拟合的过程中改变多项式的参数个数求解系数:
- 训练误差和测试误差与模型复杂度的关系:
- 1.7正则化和交叉验证
- 1.8泛化能力
- 1.9生成模型和判别模型
- 1.10监督学习的应用-分类问题
- 1.11监督学习的应用-标注问题
- 1.12监督学习的应用-回归问题
1.1统计学习的特点

1.2统计学习方法步骤

1.3 统计学习的分类
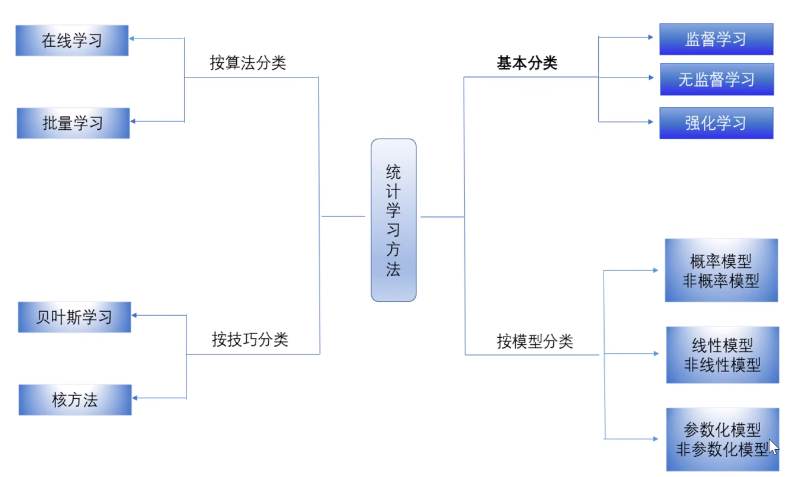
基本分类:
-
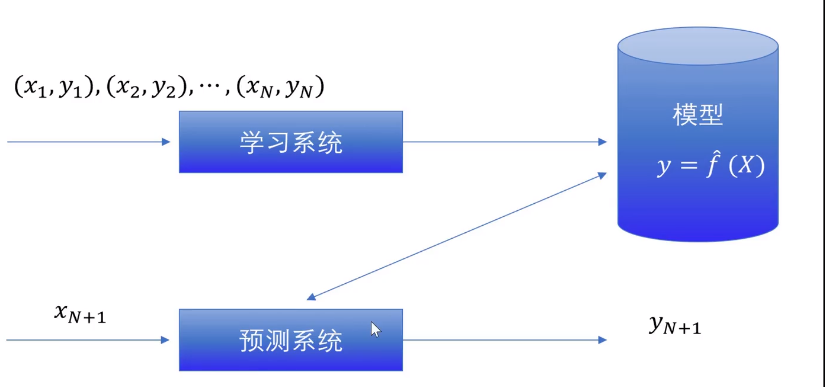
监督学习:从标注数据 中学习预测模型,学习输入到输出映射的统计规律,这一映射一模型表示
-
根据输入输出变量类型不同给予预测问题不同的名称
- 输入输出均连续:回归问题
- 输出有限个离散:分类问题
- 输入与输出均为变量序列:标注问题
-
模型形式:条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)或决策分布 Y = f ( X ) Y=f(X) Y=f(X)
-
流程图
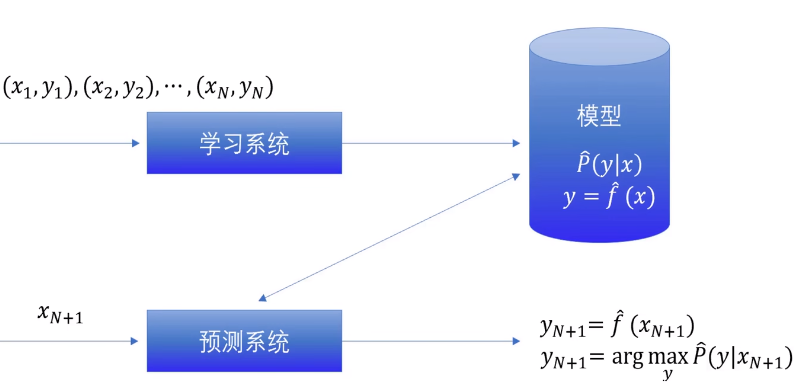
-
-
无监督学习:从无标注数据中学习预测模型的机器学习问题,学习数据中统计规律和潜在结构
- 模型形式:函数 z = g ( x ) z=g(x) z=g(x),条件概率分布 P ( z ∣ x ) P(z|x) P(z∣x)或条件概率分布 P ( x ∣ z ) P(x|z) P(x∣z)
- 流程图
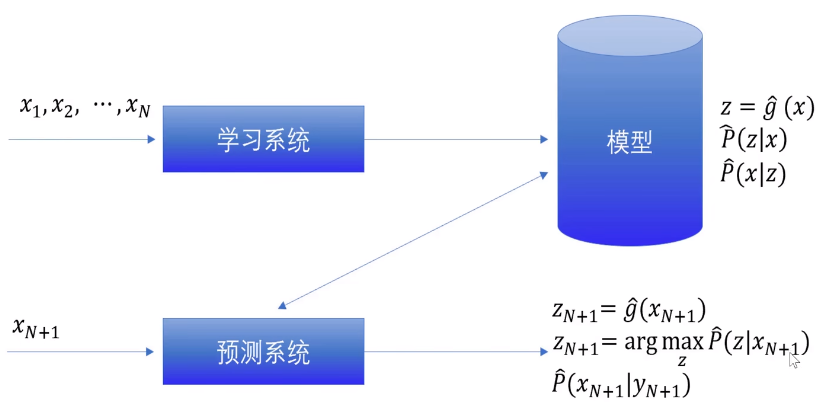
-
强化学习:智能系统在与环境的连续互动中学习最优行为策略的机器学习问题,学习最优的序贯决策
- 可以基于最优策略或最优价值得到最优模型
- 流程图
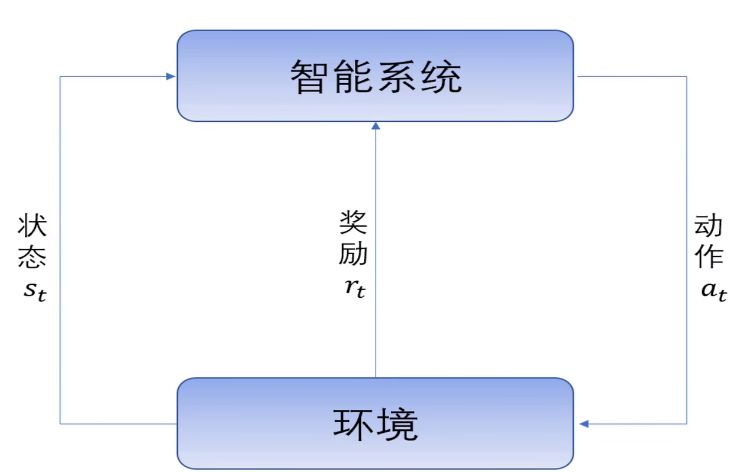
1.4 监督学习方法的三要素
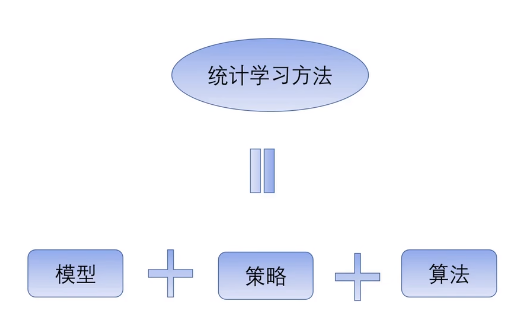
模型:条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)或决策分布 Y = f ( X ) Y=f(X) Y=f(X)
假设空间(Hypothesis Space):所有可能的条件概率分布或决策函数,假设空间模型数量一般为无限个

策略:在所有假设空间中选择一个最优模型
度量模型好坏的几个概念:
- 损失函数:
L
(
Y
,
f
(
X
)
)
L(Y,f(X))
L(Y,f(X)),非负实值函数,也称为代价函数
- 常见损失函数:

- 常见损失函数:
- 风险函数: R e x p ( f ) = E P [ L ( Y , f ( x ) ) ] = R_{exp}(f)=E_{P}[L(Y,f(x))]= Rexp(f)=EP[L(Y,f(x))]= ∫ X × Y L ( Y , f ( X ) ) P ( x , y ) d x d y \int_{X\times Y}^{}L(Y,f(X))P(x,y)dxdy ∫X×YL(Y,f(X))P(x,y)dxdy,度量平均意义下模型预测的好坏
- 经验风险: R e m p ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) R_{emp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) Remp(f)=N1∑i=1NL(yi,f(xi)),模型关于训练集的平均损失
根据大数定律,样本N趋于无穷时,经验风险趋于期望风险。但是由于现实样本数量通常是有限的,所以需要对经验风险进行一定的矫正,这就关系到监督学习的两个基本策略:经验风险最小化和结构风险最小化
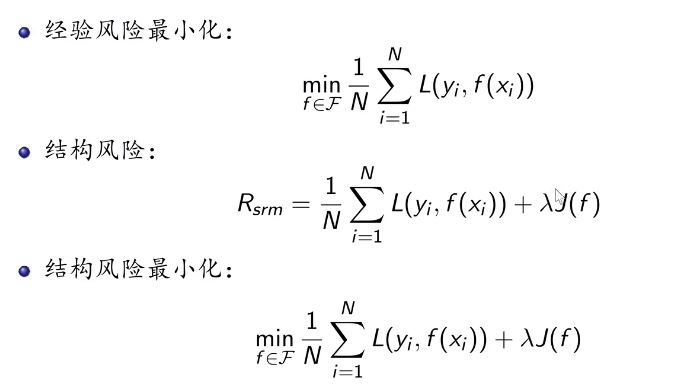
注意事项:
- 当模型是条件概率分布时,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计。
- 样本过小使用经验风险最小化会产生过拟合
- 结构风险最小化等价于正则化,是为了防止过拟合在经验风险基础上加上表示模型复杂度的正则化项或罚项
- 模型复杂度与惩罚项呈现正相关
- 最大后验概率估计等价于模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示的结构风险最小化
算法:学习模型的具体计算方法
1.5 训练误差与测试误差



1.6过拟合与模型选择
在多项式拟合的过程中改变多项式的参数个数求解系数:
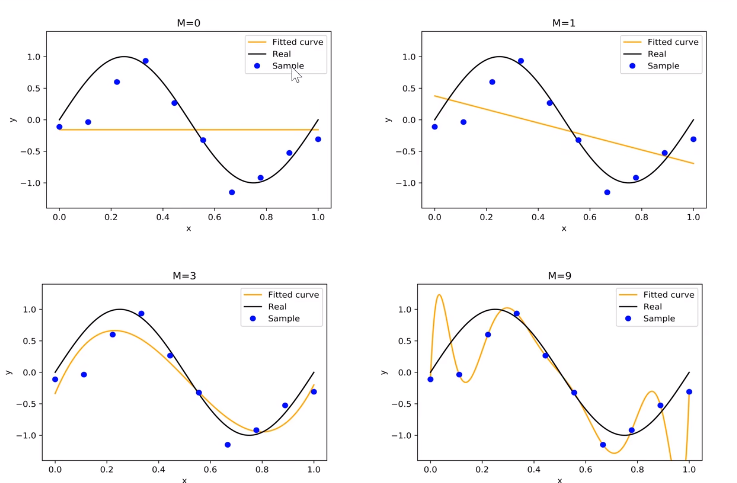
过拟合就是参数过多,对已知数据预测很好,但对未知数据预测很差的现象
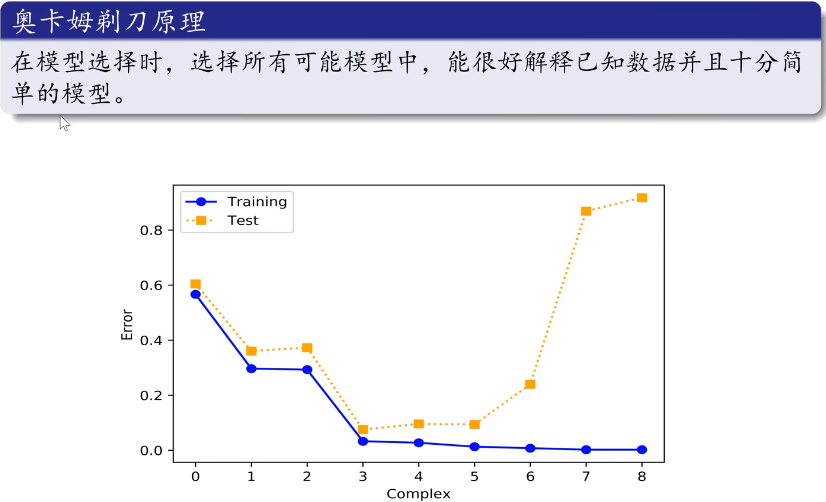
训练误差和测试误差与模型复杂度的关系:
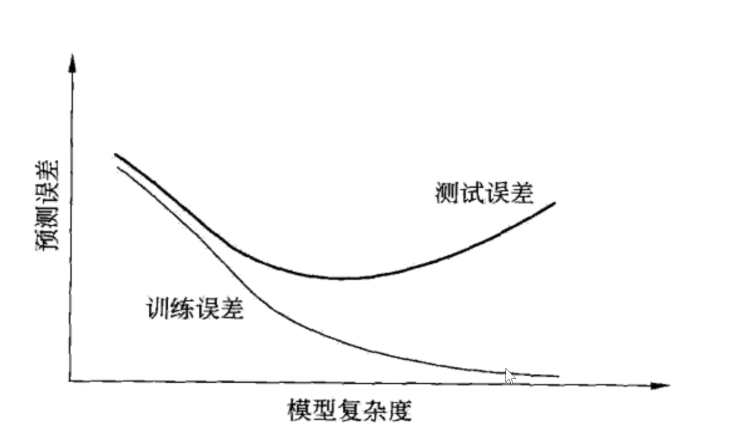
要选择训练误差和测试误差都比较小的参数个数
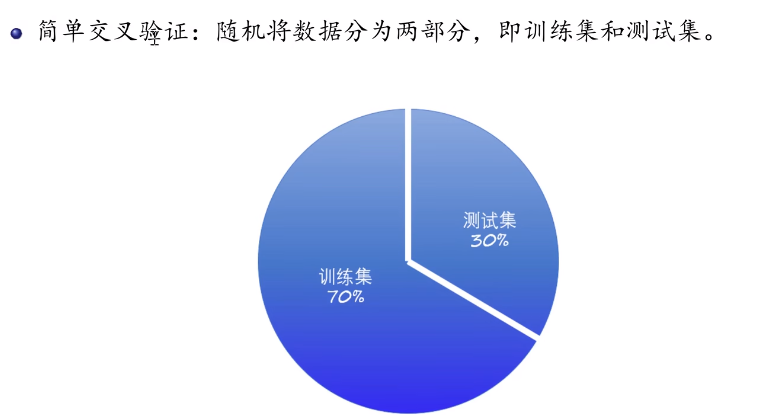
1.7正则化和交叉验证

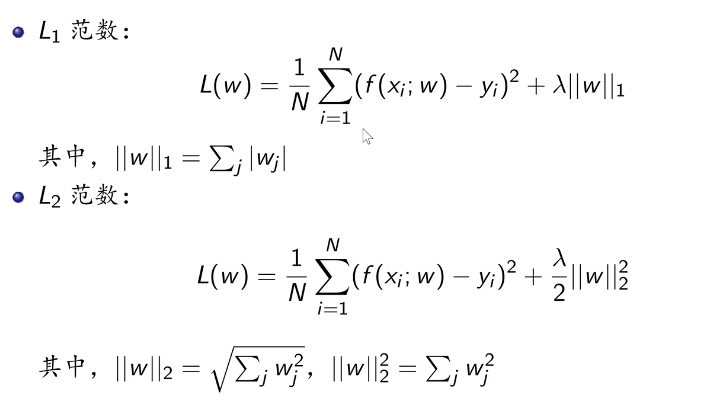

1.8泛化能力


泛化能力定理证明(二分类问题)

1.9生成模型和判别模型



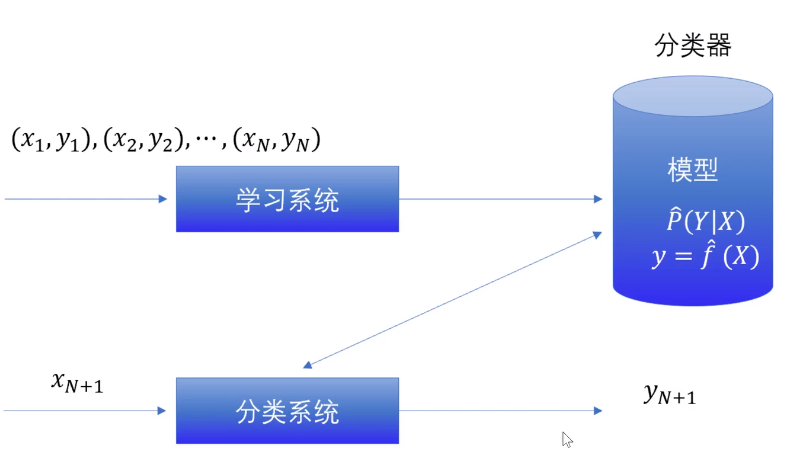
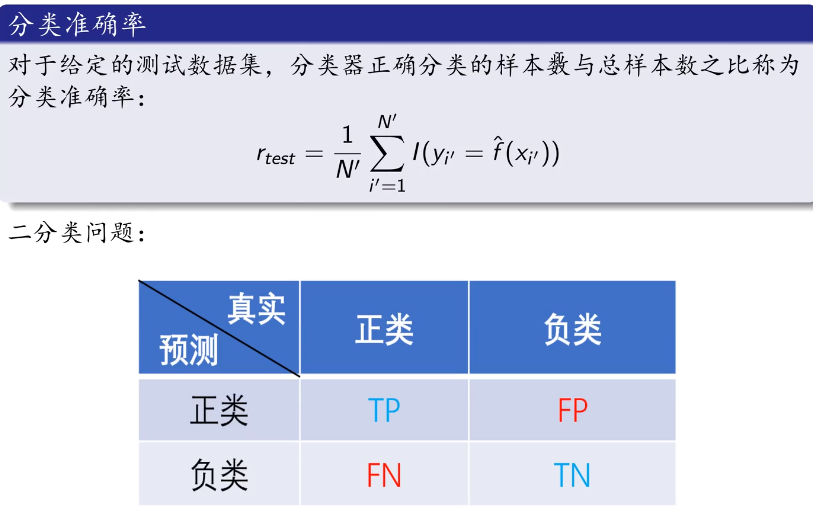
1.10监督学习的应用-分类问题


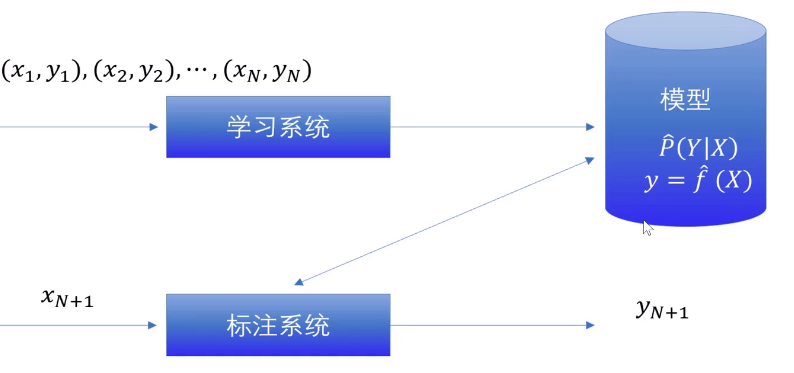
1.11监督学习的应用-标注问题


1.12监督学习的应用-回归问题