跳表

对链表进行改造，在链表上加多级索引的结构就是跳表，使其可以支持类似“二分”的查找算法。

跳表是一种各方面性能都比较优秀的动态数据结构，可以支持快速地插入、删除、查找操作，时间复杂度都为O(logn)，写起来也不复杂，甚至可以替代红黑树（Red-black tree）。

应用场景：Redis 中的**有序集合（Sorted Set）**就是用跳表来实现的。

• Redis 中的有序集合支持的核心操作：

  • 插入一个数据；

  • 删除一个数据；

  • 查找一个数据；

  • 迭代输出有序序列；

  • 按照区间查找数据（比如查找值在[100, 356]之间的数据）；

    对于按照区间查找数据这个操作，跳表可以做到 O(logn) 的时间复杂度定位区间的起点，然后在原始链表中顺序往后遍历就可以了。这样做非常高效。

"""
    An implementation of skip list.
    The list stores positive integers without duplicates.

    跳表的一种实现方法。
    跳表中储存的是正整数，并且储存的是不重复的。

    Author: Wenru
"""

from typing import Optional
import random


class ListNode:

    def __init__(self, data: Optional[int] = None):
        self._data = data
        self._forwards = []  # Forward pointers


class SkipList:
    _MAX_LEVEL = 16

    def __init__(self):
        self._level_count = 1
        self._head = ListNode()
        self._head._forwards = [None] * type(self)._MAX_LEVEL

    def find(self, value: int) -> Optional[ListNode]:
        p = self._head
        for i in range(self._level_count - 1, -1, -1):  # Move down a level
            while p._forwards[i] and p._forwards[i]._data < value:
                p = p._forwards[i]  # Move along level

        return p._forwards[0] if p._forwards[0] and p._forwards[0]._data == value else None

    def insert(self, value: int):
        level = self._random_level()
        if self._level_count < level: self._level_count = level
        new_node = ListNode(value)
        new_node._forwards = [None] * level
        update = [self._head] * level  # update is like a list of prevs

        p = self._head
        for i in range(level - 1, -1, -1):
            while p._forwards[i] and p._forwards[i]._data < value:
                p = p._forwards[i]

            update[i] = p  # Found a prev

        for i in range(level):
            new_node._forwards[i] = update[i]._forwards[i]  # new_node.next = prev.next
            update[i]._forwards[i] = new_node  # prev.next = new_node

    def delete(self, value):
        update = [None] * self._level_count
        p = self._head
        for i in range(self._level_count - 1, -1, -1):
            while p._forwards[i] and p._forwards[i]._data < value:
                p = p._forwards[i]
            update[i] = p

        if p._forwards[0] and p._forwards[0]._data == value:
            for i in range(self._level_count - 1, -1, -1):
                if update[i]._forwards[i] and update[i]._forwards[i]._data == value:
                    update[i]._forwards[i] = update[i]._forwards[i]._forwards[
                        i]  # Similar to prev.next = prev.next.next

    def _random_level(self, p: float = 0.5) -> int:
        level = 1
        while random.random() < p and level < type(self)._MAX_LEVEL:
            level += 1
        return level

    def __repr__(self) -> str:
        values = []
        p = self._head
        while p._forwards[0]:
            values.append(str(p._forwards[0]._data))
            p = p._forwards[0]
        return "->".join(values)


if __name__ == "__main__":
    l = SkipList()
    for i in range(10):
        l.insert(i)
    print(l)
    p = l.find(7)
    print(p._data)
    l.delete(3)
    print(l)

跳表的由来

单链表的查找效率太低

对于一个单链表来讲，即便链表中存储的数据是有序的，如果我们要想在其中查找某个数据，也只能从头到尾遍历链表。这样查找效率就会很低，时间复杂度会很高，是 O(n)。

提高单链表的查找效率

当链表的长度n比较大时，比如 1000、10000 的时候，在构建索引之后，查找效率的提升就会非常明显。

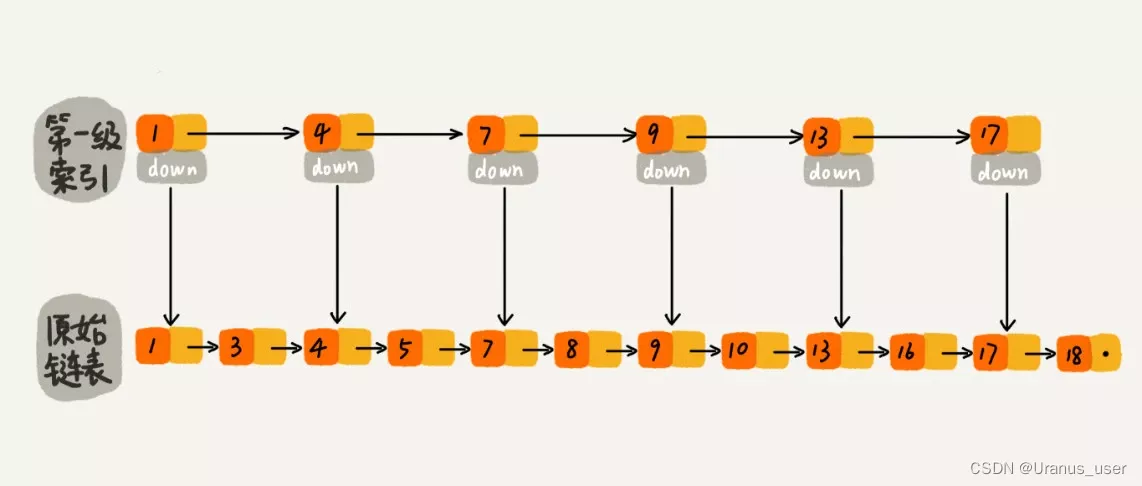
• 建立一级索引

  每两个结点提取一个结点到上一级，我们把抽出来的那一级叫做索引或索引层。

  如果我们现在要查找某个结点，比如 16。我们可以先在索引层遍历，当遍历到索引层中值为 13 的结点时，我们发现下一个结点是 17，那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针，下降到原始链表这一层，继续遍历。这个时候，我们只需要再遍历 2 个结点，就可以找到值等于 16 的这个结点了。这样，原来如果要查找 16，需要遍历 10 个结点，现在只需要遍历 7 个结点。

  加来一层索引之后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了。

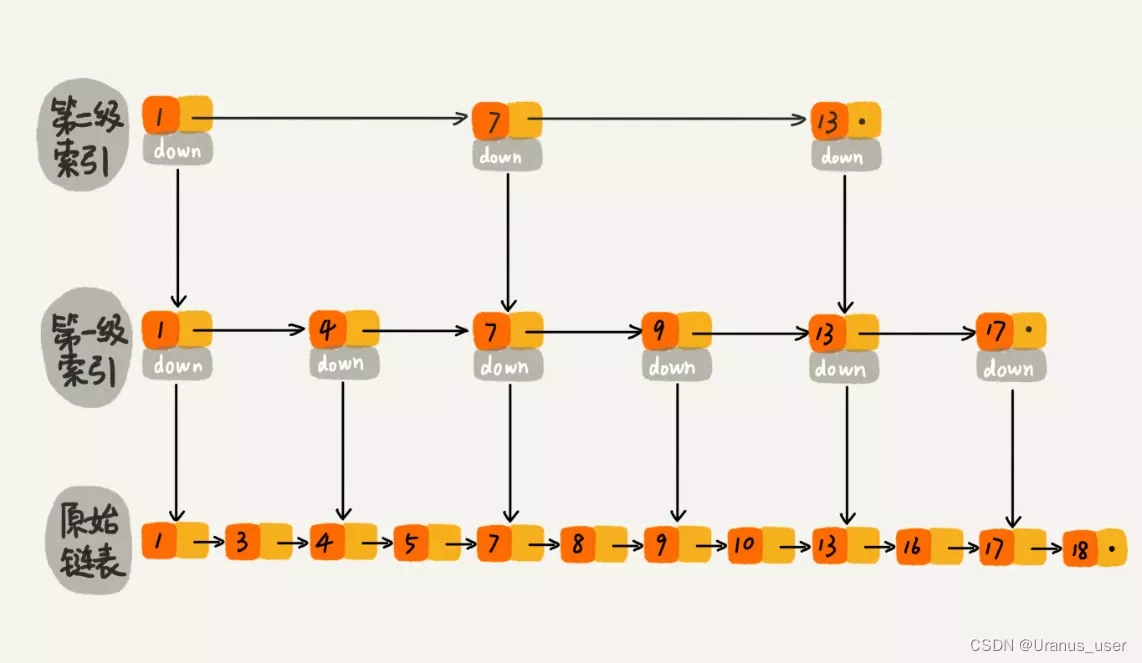
• 建立二级索引

  跟前面建立第一级索引的方式相似，我们在第一级索引的基础之上，每两个结点就抽出一个结点到第二级索引。

跳表的时间复杂度分析

跳表中查询任意数据的时间复杂度就是 O(logn)。

这个查找的时间复杂度跟二分查找是一样的。换句话说，我们其实是基于单链表实现了二分查找

这种查询效率的提升，前提是建立了很多级索引，是空间换时间的设计思路。

跳表的空间复杂度分析

假设原始链表大小为 n，那第一级索引大约有 n/2 个结点，第二级索引大约有 n/4 个结点，以此类推，每上升一级就减少一半，直到剩下 2 个结点。

如果我们把每层索引的结点数写出来，就是一个等比数列。这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是 O(n)。

实际上，在软件开发中，我们不必太在意索引占用的额外空间。在讲数据结构和算法时，我们习惯性地把要处理的数据看成整数，但是在实际的软件开发中，原始链表中存储的有可能是很大的对象，而索引结点只需要存储关键值和几个指针，并不需要存储对象，所以当对象比索引结点大很多时，那索引占用的额外空间就可以忽略了。

跳表的插入操作

对于纯粹的单链表，需要遍历每个结点，来找到插入的位置。但是，对于跳表来说，我们讲过查找某个结点的时间复杂度是 O(logn)，所以这里查找某个数据应该插入的位置，方法也是类似的，时间复杂度也是 O(logn)。

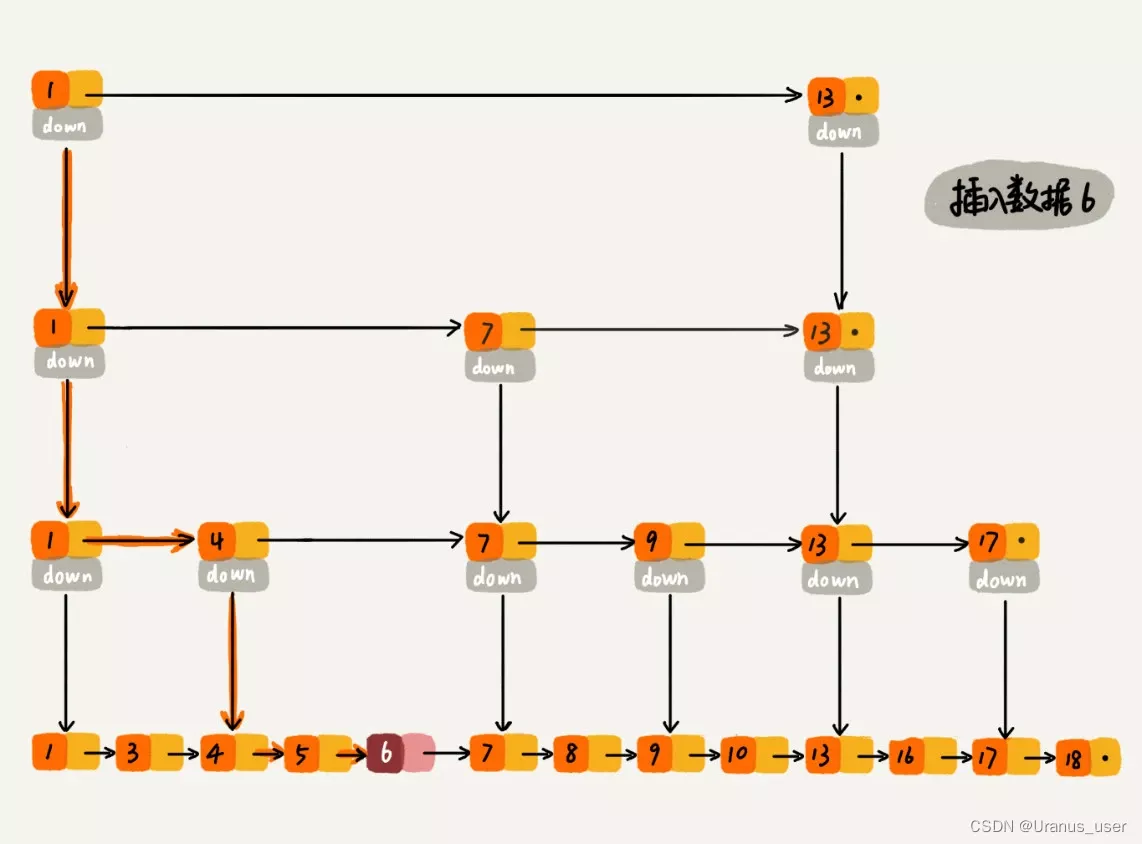
跳表的删除操作

跳表索引动态更新

• 索引需要更新的原因 - 避免操作性能下降

  当我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下，跳表还会退化成单链表。

  作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操作性能下降。

• 索引动态更新的方法

  跳表是通过随机函数来维护前面提到的“平衡性”。

  当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。通过一个随机函数，来决定将这个结点插入到哪几级索引中。