目录
- 1、算法的概念
- 1.1 举例:
- 1.2 算法的五大特性:
- 1.3 时间复杂度
- 1.4 空间复杂度
- 2、数据结构
- 2.1 内存的存储结构
- 2.2 数据结构的分类
- 2.3 顺序表存储方式
- 3、链表
- 3.1链表实现
- 3.2链表的方法
- 3.3链表增加节点
- 3.4链表删除节点
- 3.5链表总结
1、算法的概念
算法与数据结构作用:大大提升程序的性能。(战役中的兵法)
数据结构:存储、组织数据的方式
相同的数据不同的组织方式就是数据结构。([老王,18,男]或者{name:‘老王’,age:18,sex:‘男’})
算法:为了实习业务目的的各种方法和思路
算法独立存在,代码只是实现算法思想的方式而已。(例如穷举法,可以C语言实现也可以python代码实现)
算法概念:
1.1 举例:
若a+b+c =1000,且a^2+b ^2 =c ^2,如何求出所有abc的可能组合
#穷举法
#1,列举所有可能取值,2,判断是否满足条件
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
if a**2+b**2 == c**2 and a+b+c==1000:
print('a b c:',a,b,c)
end_time = time.time()
cost_time = end_time-start_time
print(cost_time)
统计运行的时间:time.time()
1.2 算法的五大特性:
- 输入。0个或多个输入
- 输出。算法至少有1个或者多个输出
- 有穷性:算法在有限的步骤之后会自动结束而不会无限循环,并且每一个步骤可以在可接受的时间内完成
- 确定性:算法中的每一步都有确定的含义,不会出现二义性
- 可行性:算法的每一步都是可行的,即每一步都能够执行有限次数完成
#方法二:在知道abc关系了,所以不用再对c遍历
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
c= 1000-a-b
if a**2+b**2 == c**2 :
print('a b c:',a,b,c)
end_time = time.time()
cost_time = end_time-start_time
print(cost_time)
实现算法程序的执行时间可以反应出算法的优劣
代码执行总时间 = 操作步骤数量*操作步骤执行时间
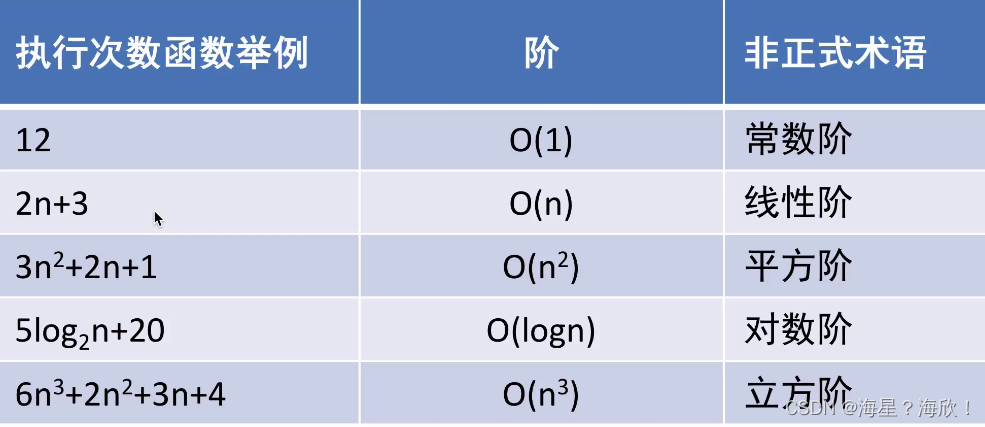
1.3 时间复杂度


时间复杂度可以表示一个算法随着问题规模不断变化的最主要趋势
衡量到算法的量级即可。大O记法
方法一的时间复杂度:T(n) = O(n^3)
方法二的时间复杂度:T(n) = O(n^2)

最优时间复杂度:算法完成工作最少需要多少基本操作。价值不大
最坏时间复杂度:算法完成工作最多需要多少基本操作。一种保证
平均时间复杂度:算法完成工作平均需要多少基本操作。一种全面评价


1.4 空间复杂度
空间复杂度:一个算法在运行过程中临时占用存储空间大小的度量
算法的时间复杂度和空间复杂度合称为算法的复杂度
2、数据结构
数据结构作用:数据结构是存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。

数据结构:静态的描述了数据元素之间的关系
高效的程序需要需要在数据结构的基础上设计和选择算法
算法是为了解决实际问题而设计的,数据结构是算法需要处理问题的载体
数据结构+算法 = 程序
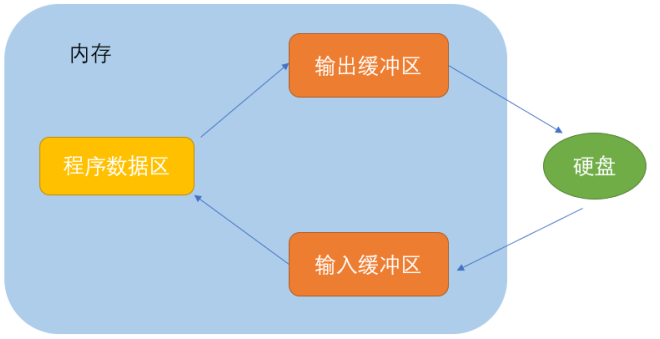
2.1 内存的存储结构
内存是以字节为基本存储单位的(1024b=1kb),每个基本存储空间都有自己的地址。内存地址是连续的
整型:占4个字节
字符:1个字节
2.2 数据结构的分类
线性结构和非线性结构
线性结构:表中各个结点具有线性关系。(栈,队列等)
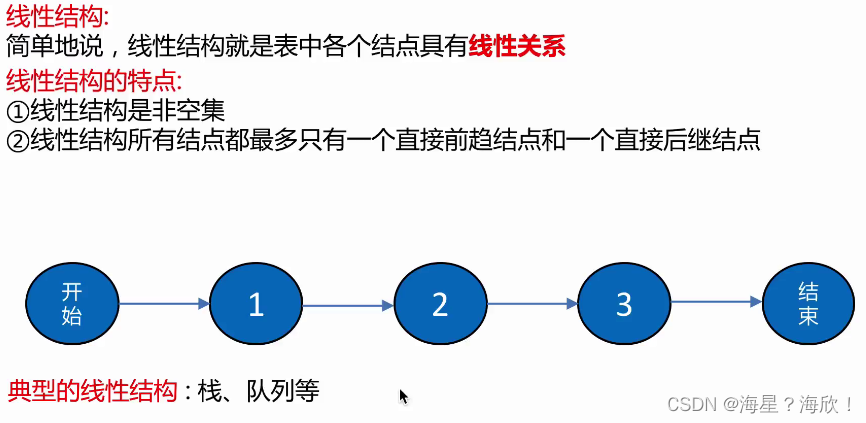
线性结构:表中各个结点具有多个对应关系。(树结构,图结构等)

2.3 顺序表存储方式
线性结构的实际存储方式,分为:顺序表和链表
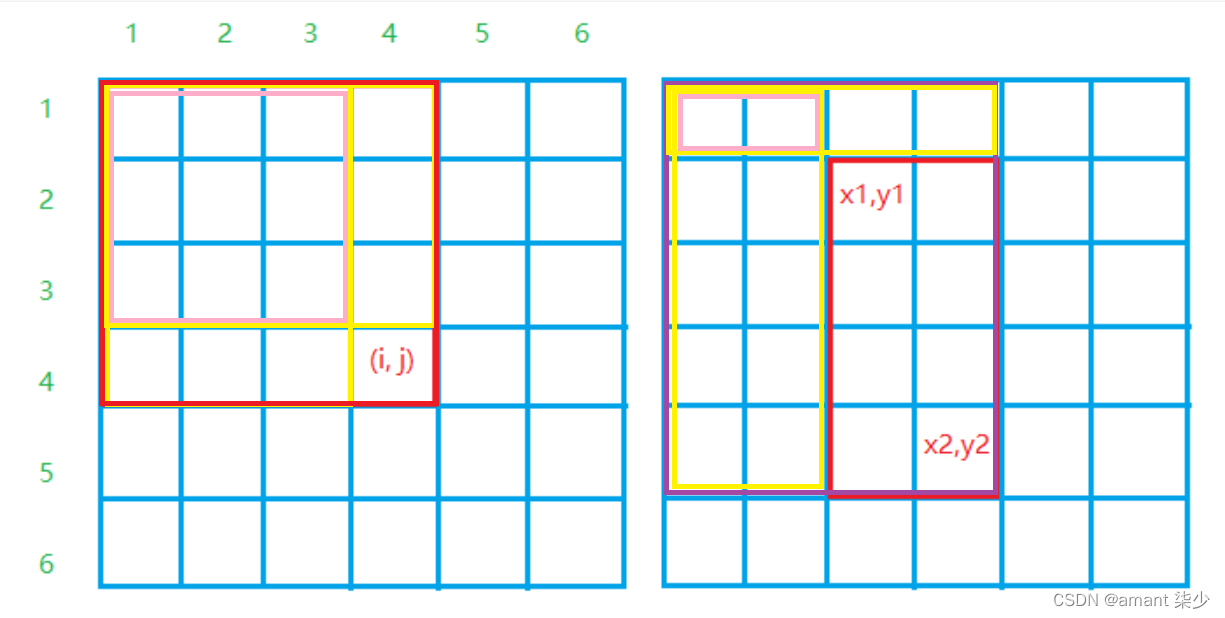
顺序表:将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由他们的存储顺序自然表示
链表:通过链接构造起来的一系列存储块中,存储区是非连续的。

顺序表存储数据的两种情况:一体式结构、分离式结构
顺序表的完整信息:数据区与信息区(元素存储区的容量和当前表中已有的元素个数)
顺序表删除元素:

3、链表
3.1链表实现
链表:不需要连续的存储空间
存储地址,保证了能找到下一个存储地址
顺序表是一个连续的存储空间

#链表结点实现
class SingleNode(object):
def __init__(self,item):
#item:存放元素 next:标识下一个结点
self.item = item
self.next = None
#结点
node1 = SingleNode(10)
print(node1.item)
print(node1.next)
#单链表的实现
class SingleLinkList(object):
def __init__(self,node=None):
#head:首节点
self.head=node
#链表
link1 = SingleLinkList()
print(link1.head)
link2 = SingleLinkList(node1)
print(link2.head.item) #输出10
链表:不需要连续的存储空间
实现链表:结点类;单链表类(由多个节点组成)

3.2链表的方法
链表的判空:看head是否为空
链表的长度测量:增加一个游标cur和一个计数count
链表的遍历:游标cur经过的每个元素都打印出来
#链表结点实现
class SingleNode(object):
def __init__(self,item):
#item:存放元素 next:标识下一个结点
self.item = item
self.next = None
#单链表的实现
class SingleLinkList(object):
def __init__(self,node=None):
#head:首节点
self.head=node
#判断链表是否为空
def is_empty(self):
if self.head is None:
return True
else:
return False
#获取链表长度
def length(self):
cur = self.head #游标记录当前所在位置
count = 0 #记录链表长度
while cur is not None:
cur = cur.next
count+=1
return count
#遍历链表
def travel(self):
cur = self.head
while cur is not None:
print(cur.item)
cur = cur.next
if __name__ =='__main__':
node1 = SingleNode(10)
#链表
link1 = SingleLinkList()
#判空
print(link1.is_empty())
#长度
print(link1.length())
#遍历
link1.travel()
3.3链表增加节点
三种情况:链表头部增加结点add(item)、尾部增加结点append(item)、指定位置增加结点insert(item)
1,链表头部增加结点add(item)
先新结点指向原头部
再头部head指向新结点
2,尾部增加结点append(item)
找到尾结点,让尾结点指向新结点
while cur.next is not None
cur = cur.next
cur.next = new_node
3,指定位置增加结点insert(item)
第一步:找到插入位置的前一个结点,
while count <pos:
cur = cur.next
count +=1
第二步:插入新结点
node.next = cur.next
cur.next = node
#链表结点实现
class SingleNode(object):
def __init__(self,item):
#item:存放元素 next:标识下一个结点
self.item = item
self.next = None
#单链表的实现
class SingleLinkList(object):
def __init__(self,node=None):
#head:首节点
self.head=node
#头部增加结点
def add(self,item):
#新结点存储数据
node = SingleNode(item)
node.next = self.head
self.head = node
#尾部增加结点
def append(self,item):
node = SingleNode(item)
#判断是否为空链表
if self.is_empty():
self.head = node
else:
cur = self.head
while cur.next is not None:
cur = cur.next
cur.next = node
#指定位置增加结点
def insert(self,pos,item):
#新结点
node = SingleNode(item)
if pos <=0: #头部增加新结点
self.add(item)
elif pos>=self.length(): #尾部增加新结点
self.append(item)
else:
#游标
cur = self.head
#计数
count = 0
#找到插入位置的前一个结点,
while count <pos-1:
cur = cur.next
count +=1
#插入新结点
node.next = cur.next
cur.next = node
if __name__ =='__main__':
node1 = SingleNode(10)
#链表
link1 = SingleLinkList()
#头部增加节点
link1.add(9)
#尾部增加结点
link1.append(11)
#指定位置增加结点
link1.insert(100,0)
link1.travel()
3.4链表删除节点
remove(item)删除节点
search(item)查找结点是否存在
remove()在头部找到要删除的元素:
cur = head
pre = None
while cur is not None:
if cur.item == item:
#要删除元素在头部
if cur ==head:
head = cur.next
#要删除元素不在头部
else:
pre.next = cur.next
return
#链表结点实现
class SingleNode(object):
def __init__(self,item):
#item:存放元素 next:标识下一个结点
self.item = item
self.next = None
#单链表的实现
class SingleLinkList(object):
def __init__(self,node=None):
#head:首节点
self.head=node
#删除节点
def remove(self,item):
cur = self.head #游标
while cur is not None:
if cur.item ==item: #找到了删除元素
if cur == self.head: #要删除的在头部
self.head = cur.next
else: #要删除的不在头部
pre.next = cur.next
return
else: #没找到要删除元素
pre = cur
cur = cur.next
#查找结点是否存在
def search(self,item):
cur = self.head
while cur is not None:
if cur.item ==item:
return True
cur= cur.next
return False
if __name__ =='__main__':
node1 = SingleNode(10)
#链表
link1 = SingleLinkList()
#头部增加节点
link1.add(9)
#尾部增加结点
link1.append(11)
#指定位置增加结点
link1.insert(100,0)
link1.travel()
#删除元素
link1.remove(9)
link1.travel()
#查找结点是否存在
print(link1.search(11))
print(link1.search(9))
3.5链表总结
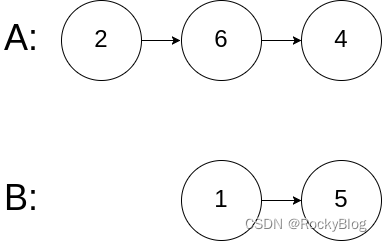
线性结构:最多只能有一个前驱结点和一个后继结点
非线性结构:可以有多个前驱结点和一个后继结点
线性结构:顺序表、链表
顺序表:元素顺序地存放在一块连续的存储区里,元素间的顺序关系由他们的存储顺序自然表示
链表:将元素存放在通过链接构造起来的一系列存储块中,存储空间非连续