随机分布模型

前言

本文首先结合自身研究经验，在前言部分简单叙述自己对随机概念的理解，描述可能不是很专业，仅供参考。正文部分重点描述常见的离散型随机变量以及连续性随机变量的分布类型，这部分参考各方资料，如果问题，欢迎评论区具体指出。

个人认为目前随机概念更多的是对结果的描述，人们往往容易忽略产生这种随机结果的原因。以抛骰子为例，普遍认为，如果随机抛出骰子，每次投出结果是不同的，我们把这种输出结果看似随机的现象认为是随机事件。

事实上，抛骰子可以认为是一种相当复杂的物理过程，其结果受抛出骰子时，手对骰子的力，所处环境中的重力，骰子飞行过程受到的阻力以及骰子碰撞地面的受力情况等诸多因素的影响。我们尝试对抛骰子这样一个物理过程进行精准建模，在抛骰子过程中，如果我们能够弄清楚影响骰子结果的所有要素，并且也能在投骰子过程精确的保证所有要素在每次实验都能一致，是否意味着每次实验结果都能惊人的一致。

问题是对抛骰子过程的建模是非常困难的，一方面整个物理过程影响要素很多，碰撞方面机理或许不是完全清楚，另一方面，很难保证抛骰子的力度以及角度完全确定。因此，目前的研究是将其作为一个黑盒子模型进行研究，模型输入是随机抛出骰子，投出骰子的状态、使出的力度、投出的角度凭借试验者的经验进行，这样就可以对模型输出的结果进行研究，并基于概率统计原理对结果进行分析。

由于结果随机出现的特性，投骰子被运用到赌博上，一些人为了得到想要的结果上，一方面，有些人可能会在大量投骰子训练过程中找到投出特定点数的手感，以此大幅提高投出特定点数的概率；另一方面，有些人会对骰子进行改造，如改变骰子重心（利用重心越低，物理状态越稳定的规律），使其投出特定点数的概率大大提升。

上述论述多是自己的遐想，感兴趣的读者可以以此来对随机概念进行新的思考。有些随机过程并不像投骰子那样可以轻易改变分布类型，如接收机中的热噪声，或者说产生各种随机现象的机理并不容易研究，而我们又急需从随机的结果中获取所需的信息（个人感觉有点像现在的人工智能，机器学习），因此，人们巧妙的避开机理上的问题，用统计结果的分布特点来描述整个过程，利用少数的统计参量依概率描述复杂的模型准确性。为了更加严谨描述随机现象，随机结果用随机变量描述，并根据结果特点分为离散型随机变量和连续性随机变量，下面简单介绍。

一、离散型随机变量

1.1 0-1分布

0-1分布又称两点分布或伯努利（ Bernoulli）分布，试验结果只有两个（如成功、失败）。设随机变量X 只取 0或 1两个值，它的分布律为

$P\left \{ X=k \right \}=p^{k}(1-p)^{1-k}\, \, \, \, \, \, \, \, \, \, \, k=0,1$

则称随机变量 X 服从参数为 p的（0 —1）分布，记作 $X\sim b\left ( 1,p \right )$ 。

均值

$E\left ( X \right )=\sum_{k=0}^{1}kp^{k}(1-p)^{1-k}=p$

方差

$D\left ( X \right )=E\left [ \left ( X-E\left ( X \right ) \right )^{2} \right ]=\sum_{k=0}^{1}\left (k-p \right )^{2}p^{k}(1-p)^{1-k}=p\left ( 1-p \right )$

1.2 二项分布

重复地进行 n 次独立伯努利试验（“重复” 是指这个试验中各次试验条件相同，“独立”是指各次试验的结果互不影响），结果为1的试验次数服从二项分布。设随机变量X 的所有可能值为0, 1, 2，… ，n, 其分布律为

$P\left ( X=k \right )=C_{n}^{k}p^{k}(1-p)^{n-k}\, \, \, \, \, \, \, \, \, \, \, k=0,1,\cdots ,n$

则称随机变量 X 服从参数为 p的（0 —1）分布，记作 $X\sim b\left ( n,p \right )$

均值

$E\left ( X \right )=\sum_{k=0}^{n}kC_{n}^{k}p^{k}(1-p)^{n-k}=np\sum_{k=1}^{n}kC_{n-1}^{k-1}p^{k-1}(1-p)^{n-k}=np$

方差

$E\left ( X^{2} \right )=E\left [ X\left ( X-1 \right ) \right ]+E\left ( X \right )\\=\sum_{k=0}^{n}k\left ( k-1 \right )C_{n}^{k}p^{k}(1-p)^{n-k}+np\\=n\left ( n-1 \right )p^{2}\sum_{k=2}^{n}C_{n-2}^{k-2}p^{k-2}(1-p)^{n-k}+np\\=n\left ( n-1 \right )p^{2}+np$

$D\left ( X \right ) =E\left ( X^{2} \right )-\left [ E\left ( X \right ) \right ]^{2}=np\left ( 1-p \right )$

1.3 帕斯卡分布

在重复、独立的伯努利试验，设每次试验成功的概率为p，失败的概率为q= 1- p，若将试验进行到出现r(r为常数)次成功为止，以随机变量X表示所需试验次数，则 X是离散型随机变量, 其分布律为为：

$P\left ( X=k \right )=C_{k-1}^{r-1}p^{r}(1-p)^{k-r}\, \, \, \, \, \, \, \, \, \, \, k=r,r+1,\cdots$

则称随机变量 X 服从参数为 p，r的几何分布，记作 $X\sim NB\left ( r,p \right )$

均值

$E\left ( X \right )=\sum_{k=0}^{n}kC_{k-1}^{r-1}p^{r}(1-p)^{k-r}=\frac{r}{p}$

方差

$D\left ( X \right )=E\left [ \left ( X-E\left ( X \right ) \right )^{2} \right ]=\frac{r\left ( 1-p \right )}{p^{2}}$

1.4 几何分布

重复进行随机事件，直到事件发生为止才停下,X 为首次发生时共做的事件的次数。设随机变量X 的所有可能值为1, 2，… ，其分布律为

$P\left ( X=k \right )=p(1-p)^{k-1}\, \, \, \, \, \, \, \, \, \, \, k=1,2,\cdots$

则称随机变量 X 服从参数为 p的几何分布，记作 $X\sim GE\left ( n,p \right )$

均值

$E\left ( X \right ) =\sum_{k=1}^{\infty }kp(1-p)^{k-1}=p\sum_{k=1}^{\infty }k(1-p)^{k-1}=p\frac{1}{p^{2}}=\frac{1}{p}$

方差

$E\left ( X^{2} \right )=\sum_{k=0}^{\infty }k^{2}p(1-p)^{k-1}=\frac{1+q}{p^{2}}$

$D\left ( X \right ) =E\left ( X^{2} \right )-\left [ E\left ( X \right ) \right ]^{2}=\frac{1-p}{p^{2}}$

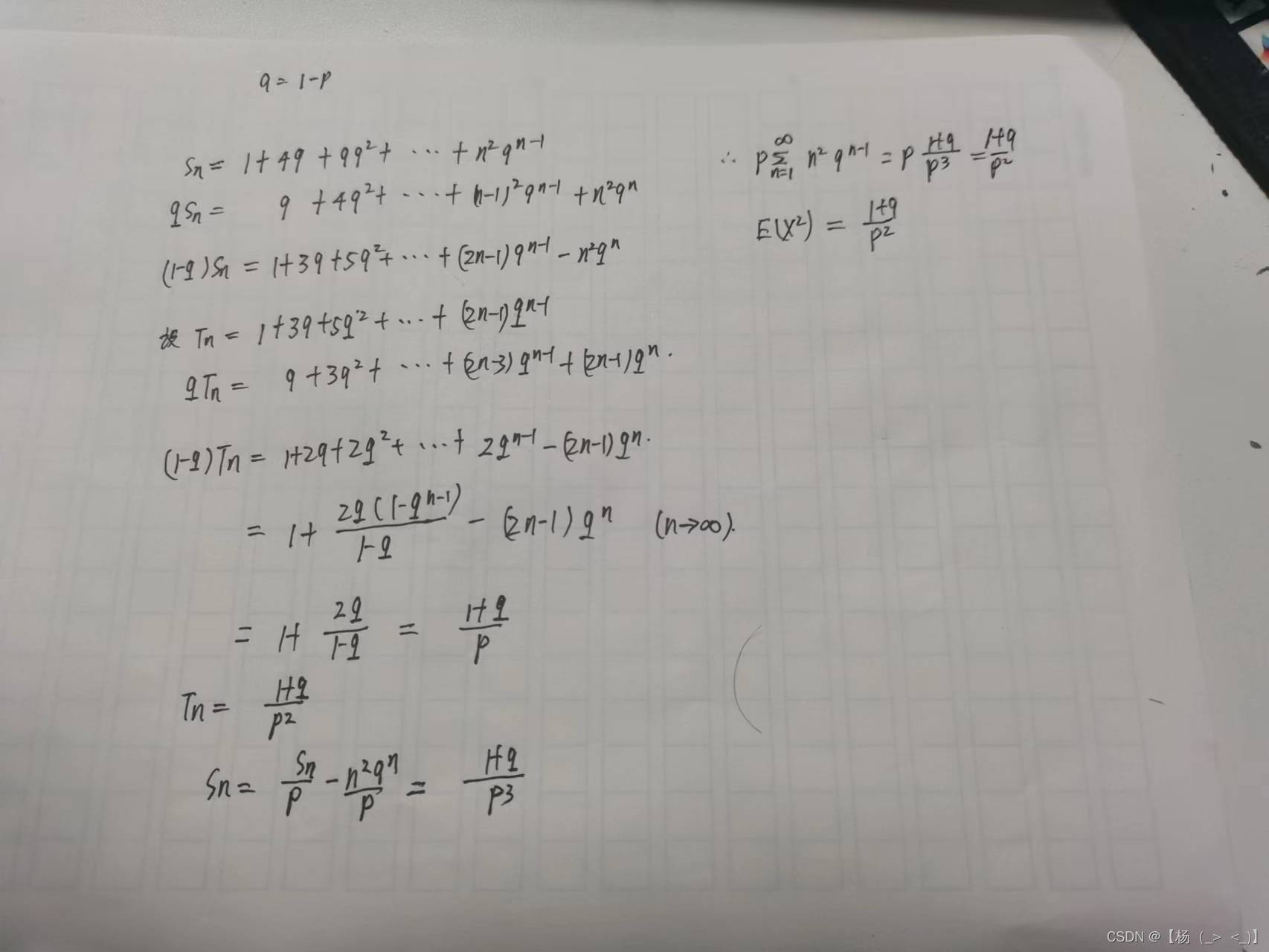
1.5 超几何分布

N 个产品，其中 M 个次品，从中任取 n 个。 X 为这 n 个中的次品数，则 X∼H(n,M,N) 。分布律为：

$P\left ( X=k \right )=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}}\, \, \, \, \, \, \, \, \, \, \, k=0,1,\cdots,M$

均值

$E\left ( X \right )=\sum_{k=0}^{n}kC_{k-1}^{r-1}p^{r}(1-p)^{k-r}=n\frac{M}{N}$

方差

$D\left ( X \right )=E\left [ \left ( X-E\left ( X \right ) \right )^{2} \right ]=\frac{nM}{N}\frac{N-M}{N}\frac{N-n}{N-1}$

1.6 泊松分布

设随机变量X 的所有可能值为0, 1, 2，… ，其分布律为

$P\left ( X=k \right )=\frac{\lambda ^{k}}{k!}e^{-\lambda }\, \, \, \, \, \, \, \, \, \, \, k=0,1,\cdots$

其中 $\lambda >0$ 是常数，则称X 服从参数为 $\lambda$ 的泊松分布，记作 $X\sim \pi\left ( \lambda \right )$

均值

$E\left ( X \right ) =\sum_{k=0}^{\infty }k\frac{\lambda ^{k}}{k!}e^{-\lambda }=\lambda\sum_{k=1}^{\infty }\frac{\lambda ^{k-1}}{\left ( k-1 \right )!}e^{-\lambda }=\lambda$

方差

$E\left ( X^{2} \right )=E\left [ X\left ( X-1 \right ) \right ]+E\left ( X \right )\\=\sum_{k=0}^{\infty }k\left ( k-1 \right )\frac{\lambda ^{k}}{k!}e^{-\lambda }+\lambda\\=\lambda^{2}e^{-\lambda }\sum_{k=2}^{\infty }\frac{\lambda ^{k-2}}{\left ( k-2 \right )!}+\lambda\\=\lambda^{2}+\lambda$

$D\left ( X \right ) =E\left ( X^{2} \right )-\left [ E\left ( X \right ) \right ]^{2}=\lambda$

二、连续型随机变量

2.1 均匀分布

概率密度函数

$f\left ( x \right )=\left\{\begin{matrix} \frac{1}{b-a} & x\in \left ( a,b \right )\\ 0 & else \end{matrix}\right.$

均值

$E\left ( X \right ) =\int_{-\infty }^{\infty }xf\left ( x \right )dx=\frac{a+b}{2}$

方差

$E\left ( X^{2} \right ) =\int_{-\infty }^{\infty }x^{2}f\left ( x \right )dx=\frac{a^{2}+ab+b^{2}}{3}$

$D\left ( X \right ) =E\left ( X^{2} \right )-\left [ E\left ( X \right ) \right ]^{2}=\frac{\left ( b-a \right )^{2}}{12}$

2.2 指数分布

概率密度函数

$f\left ( x \right )=\lambda e^{-\lambda x}\, \, \, \, \, \, \, \, \, \, x>0$

均值

$E\left ( X \right ) =\int_{-\infty }^{\infty }x\lambda e^{-\lambda x}dx=\frac{1}{\lambda }$

方差

$E\left ( X^{2} \right ) =\int_{-\infty }^{\infty }x^{2}f\left ( x \right )dx=\frac{2}{\lambda ^{2}}$

$D\left ( X \right ) =E\left ( X^{2} \right )-\left [ E\left ( X \right ) \right ]^{2}=\frac{1}{\lambda ^{2}}$

2.3 高斯分布/正态分布

概率密度函数

$f\left ( x \right )=\frac{1}{\sqrt{2\pi \sigma ^{2}}} e^{-\frac{\left ( x-\mu \right )}{2\sigma ^{2}}}$

均值

$E\left ( X \right ) =\int_{-\infty }^{\infty }xf\left ( x \right )dx=\mu$

方差

$D\left ( X\right ) =\int_{-\infty }^{\infty }\left ( x-\mu \right )^{2}f\left ( x \right )dx=\sigma ^{2}$

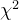2.4 $\chi ^{2}$ 分布（抽样分布）

设X1, X2, … , Xn是来自总体N(0,1)的样本, 则称统计量：

$\chi ^{2}=X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2}$

服从自由度为 n 的 $\chi ^{2}$ 分布。概率密度函数

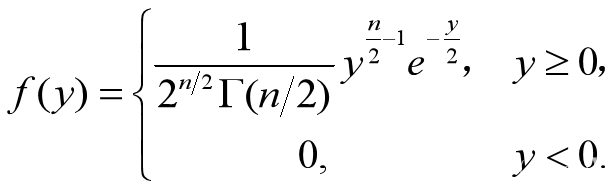
其中伽玛函数 $\Gamma \left ( \alpha \right )$

均值

$E\left ( Y \right ) =\int_{-\infty }^{\infty }yf\left ( y \right )dx=n$

方差

$D\left ( Y \right ) =\int_{-\infty }^{\infty }\left ( y-n \right )^{2}f\left ( y \right )dx=2n$

2.5 t分布（抽样分布）

设X～N(0,1) , Y～ $\chi ^{2}\left ( n \right )$ , 且X与Y相互独立，则称随机变量

$t =\frac{X}{\sqrt{Y/n}}$

服从自由度为 n的 t 分布.t 分布又称学生氏(student)分布.概率密度函数

均值

$E\left ( t \right ) =\int_{-\infty }^{\infty }tf\left ( t \right )dx=0$

方差

$D\left ( t \right ) =\int_{-\infty }^{\infty }\left ( t-0 \right )^{2}f\left ( t \right )dx=\frac{n}{n-2}$

2.6 F分布（抽样分布）

设 $U\sim \chi ^{2}\left ( n_{1} \right )$ 与 $V\sim \chi ^{2}\left ( n_{2} \right )$ ，U与V相互独立，则称随机变量

$F=\frac{U/n_{1}}{V/n_{2}}$

服从自由度为n1及 n2 的F分布，n1称为第一自由度，n2称为第二自由度。概率密度为

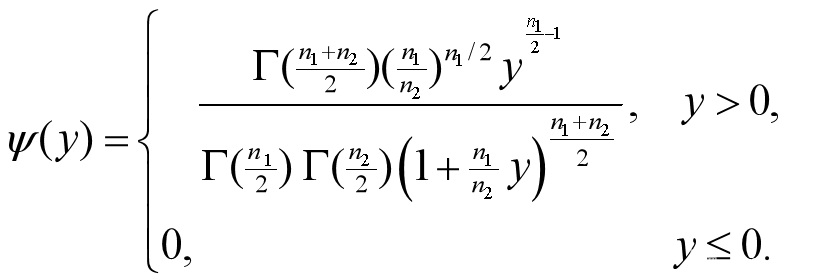
均值

$E\left ( y\right ) =\frac{n}{n-2}\, \, \, \, \, \, \, \, \, \, r=1,n>2$

方差

$D\left ( y\right ) =\frac{2n^{2}\left ( m+n-2 \right )}{m\left ( n-2 \right )^{2}\left ( n-4 \right )}\, \, \, \, \, \, \, \, \, \, n>4$

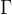2.7 $\Gamma$ 分布

假设随机变量X为等到第α件事发生所需之等候时间，且每个事件之间的等待时间是互相独立的，α为事件发生的次数，β代表事件发生一次的概率，那么这α个事件的时间之和服从伽马分布。其概率密度函数为

$f\left ( x \right )=\frac{1}{\beta ^{\alpha }\Gamma \left ( \alpha \right )} x^{\alpha -1}e^{-\frac{x}{\beta} }\, \, \, \, \, \, \, \, \, x>0$

均值

$E\left ( X\right ) =\frac{\alpha }{\beta }$

方差

$D\left ( X\right ) =\frac{\alpha }{\beta ^{2}}$

2.8 瑞利分布

当一个随机二维向量的两个分量呈独立的、均值为0，有着相同的方差的正态分布时，这个向量的模呈瑞利分布，概率密度为：

$f\left ( x \right )=\frac{x}{\sigma ^{2}} e^{-\frac{x^{2}}{2\sigma ^{2}} }\, \, \, \, \, \, \, \, \, x>0$

均值

$E\left ( X\right ) =\sqrt{\frac{\pi }{2}}\sigma$

方差

$D\left ( X\right ) =\frac{4-\pi }{2}\sigma ^{2}$

2.9 莱斯分布

瑞利分布考虑的是零均值实部虚部是独立同分布的复高斯分布，莱斯分布针对的是一般情况下的模值分布，概率密度函数为：

$f\left ( x \right )=\frac{x}{\sigma ^{2}} e^{-\frac{\left ( x^{2}+s^{2} \right )}{2\sigma ^{2}} }I_{0}\left ( \frac{xs}{\sigma ^{2}} \right )\, \, \, \, \, \, \, \, \, x>0$

$s^{2}$ 表示直视路径功率分量， $2\sigma ^{2}$ 是非直视路径功率分量。 $I_{0}$ 是修正的零阶贝塞尔函数。

$I_{0}\left (x \right )=\int_{0}^{2\pi}e^{x \cos\left ( \theta \right )}d\theta$

2.10 韦布尔分布

适用于机电类产品的磨损累计失效的分布形式。由于它可以利用概率值很容易地推断出它的，被广泛应用于各种寿命试验的数据处理。概率密度函数：

$f\left ( x \right )=\frac{k}{\lambda } \left ( \frac{x}{\lambda } \right )^{k-1}e^{-\left ( x/\lambda \right )^{k}}\, \, \, \, \, \, \, \, \, x\geq 0$

均值

$E\left ( X\right ) =\lambda \Gamma \left ( 1+\frac{1}{k} \right )$

方差

$D\left ( X\right ) =\lambda ^{2}\left [ \Gamma \left ( 1+\frac{2}{k} \right )-\Gamma \left ( 1+\frac{1}{k} \right )^{2} \right ]$

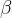2.11 $\beta$ 分布

概率密度函数

$f\left ( x \right )=\frac{\Gamma \left ( \alpha +\beta \right )}{\Gamma \left ( \alpha \right ) +\Gamma \left ( \beta \right )} x ^{\alpha -1}\left ( 1-x \right )^{\beta -1}\, \, \, \, \, \, \, \, \, 0<x< 1$

均值

$E\left ( X\right ) =\frac{\alpha }{\alpha +\beta }$

方差

$D\left ( X\right ) =\frac{\alpha \beta }{\left ( \alpha +\beta \right )^{2}\left ( \alpha +\beta +1 \right )}$

2.12 对数正态分布

概率密度函数

$f\left ( x \right )=\frac{1}{x\ln a\sqrt{2\pi\sigma ^{2}}}e^{-\frac{\left ( \log_{a}x-\mu \right )^{2}}{2\sigma ^{2}}}$

均值

$E\left ( X\right ) =a^{\mu +\ln a\sigma ^{2}/2}$

方差

$D\left ( X\right ) =\left ( a^{\ln a\sigma ^{2}} -1\right )a^{2\mu +\ln a\sigma ^{2}}$

2.13 柯西分布

概率密度函数

$f\left ( x \right )=\frac{1}{\pi }\left [ \frac{\gamma }{\left ( x-x_{0} \right )^{2}+\gamma ^{2}} \right ]$

均值和方差不存在。

三、性质及定理

3.1、均值性质

性质1：E (C ) = C

性质2：E (aX ) = a E (X )

性质3：E (X + Y ) = E (X ) + E (Y )

性质4：当X ,Y 相互独立时，E (X Y ) = E (X )E (Y )

性质5：设X 为连续型随机变量，密度函数为f (x)，Y = g(X ),若广义积分 $\int_{-\infty }^{\infty }g\left ( x \right )f\left ( x \right )dx$ 绝对收敛，则

$E\left ( Y \right )=\int_{-\infty }^{\infty }g\left ( x \right )f\left ( x \right )dx$

3.2、方差性质

性质1：若X=C，C为常数，则D(X)=0 .

性质2:若b为常数,随机变量X的方差存在，则bX的方差存在, 且D(bX) = b2D(X)

性质3：若随机变量X1, X2, … , Xn 的方差都存在，则X1+X2+...+Xn的方差存在，且

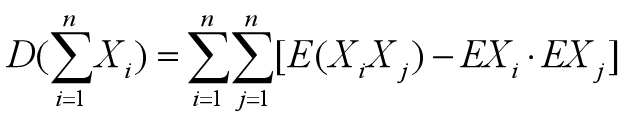
性质4：若随机变量X1, X2, …, Xn相互独立，则

性质5：有限个相互独立的正态随机变量的线性组合仍然服从正态分布

性质6：切比雪夫(Chebyshev)不等式

对随机变量X 和任意的 $\varepsilon >0$ ，有

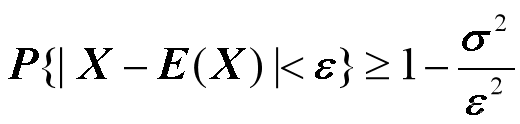
3.3、定理

辛钦大数定律

设X1, X2, …是独立同分布的随机变量序列，且E(Xi)= $\mu$ ，i=1, 2,…, 则对任给 $\varepsilon$ >0,

$\lim_{n\rightarrow \infty }P\left \{ \left | \frac{1}{n}\sum_{i=1}^{n} X_{i}-\mu \right |<\varepsilon \right \}=1$

辛钦大数定律为估计随机变量的期望值提供了一条实际可行的途径.

贝努里大数定律

设Sn是n重贝努里试验中事件A发生的次数，p是一次试验中事件A发生的概率，则对任给的ε> 0，

$\lim_{n\rightarrow \infty }P\left \{ \left | \frac{S_{n}}{n}-p \right |<\varepsilon \right \}=1$

贝努里大数定律提供了通过试验来确定事件概率的方法.

中心极限定理

设随机序列 {Xj} 独立同分布,有共同的数学期望 $\mu$ 和方差 $\sigma ^{2}$ . 部分和Sn =X1＋ X2＋…＋ Xn, 则Sn的标准化

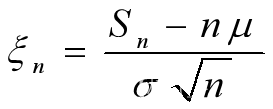
依分布收敛到标准正态分布. 即对任何x,

这里 $\Phi \left ( x \right )$ 是标准正态分布的分布函数。对充分大的n ，部分和Sn =X1＋ X2＋…＋ Xn, 的概率分布可以用正态分布

常用离散型概率分布(下) - 知乎 (zhihu.com)

概率论中，负二项分布（帕斯卡分布）的期望到底是哪个？ - 知乎 (zhihu.com)

概率论学习笔记（二） - 知乎 (zhihu.com)

F分布期望方差怎么推导? - 知乎 (zhihu.com)

Gamma分布 - 知乎 (zhihu.com)

瑞利分布（数学名词）_百度百科 (baidu.com)

什么是小尺度衰落信道、瑞利信道、莱斯信道、Nakagami信道 - 知乎 (zhihu.com)

通信原理高斯分布莱斯分布瑞利分布有何联系有何区别如何区分? - 知乎 (zhihu.com)

柯西分布_百度百科 (baidu.com)

贝塔分布_百度百科 (baidu.com)

韦布尔分布_百度百科 (baidu.com)

柯西分布_百度百科 (baidu.com)

总结

本文简单介绍了自己对随机概念的理解，并简单列举了常见的随机分布类型。在信号处理中常用的随机信号模型包括：高斯模型、瑞利模型、莱斯模型等。有更好的内容欢迎在评论区放置链接，另外有问题也欢迎评论区留言。转载请附链接【杨（_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。