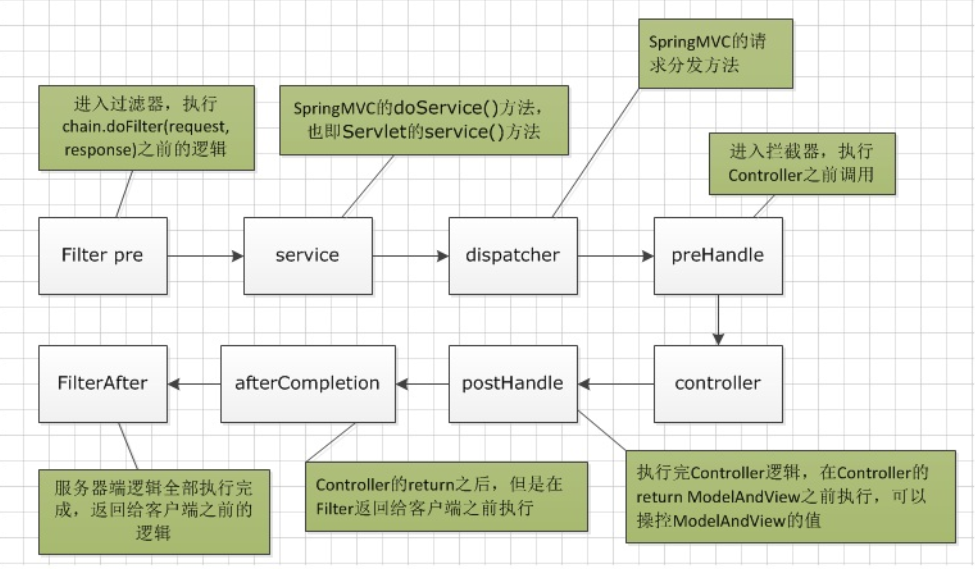
前言

上篇文章【数据结构与算法——C语言版】4. 排序算法（1）——选择排序我们介绍了排序算法中的选择排序，其时间复杂度是O(n²)，本篇文章我们将介绍另一种同样时间复杂度是O(n²)的排序算法——冒牌排序，这两种算法思路不同，但都是两层循环，实用性不高，但有必要通过讲解来掌握不同的算法思路。

冒泡排序核心思想

选择排序的核心思想是每次找到最小值并与第i个元素交换，找n次。
而冒泡排序的核心思想是每次遍历整个数组，比较相邻的两个元素arr[i]和arr[j]，将较大者放在arr[j]的位置，然后继续比较arr[j]和arr[j+1]；将数组遍历n次后（n为数组元素个数），数组升序有序。
该算法能使数组有序的核心原因如下：

从左到右，相邻元素进行比较。每次比较一轮，就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。
以从小到大排序为例，第一轮比较后，所有数中最大的那个数就会浮到最右边；第二轮比较后，所有数中第二大的那个数就会浮到倒数第二个位置……就这样一轮一轮地比较，最后实现从小到大排序。

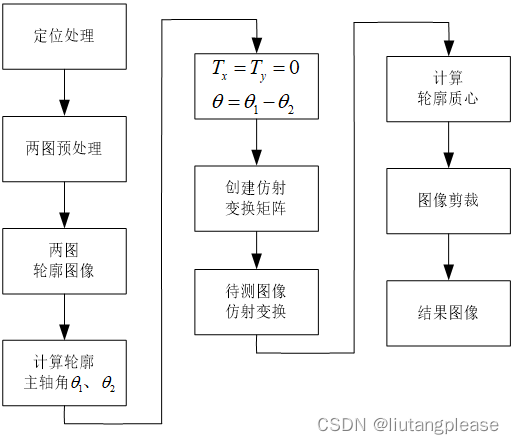
用一张图片直观的观察一下：

第一轮遍历中，总是选择最大的那个数并交换至靠右的位置，第一轮比较完成后，数组中最大的元素50就被“冒”到了右边
最后一轮遍历，arr[0]就是最小的元素2，所以最后一轮遍历没有发生交换，即数组已升序有序。

冒泡排序过程细化

我们还是用一个例子，一步步带着大家来理解冒泡排序的过程。

数组 arr[5] = {5,1,4,2,8}，如果采用冒泡排序对其进行升序（由小到大）排序，则整个排序过程如下所示：

1. 第一次遍历数组arr，两两比较arr[i]和arr[i+1]，并将较大者交换到arr[i+1]。第一次遍历前，数组 arr[5] = {5,1,4,2,8}；遍历后，数组arr[5] = {1,4,2,5,8}；此时arr[4]已经是最大值8，所以下次遍历我们只需要遍历arr[0 ~ 3]
   

2. 第二次遍历数组arr，两两比较arr[i]和arr[i+1]，并将较大者交换到arr[i+1]。第一次遍历前，数组 arr[5] = {1,4,2,5,8}；遍历后，数组arr[5] = {1,2,4,5,8}；此时arr[3]已经是次大值5，且arr[3~4]保持升序有序；所以下次遍历我们只需要遍历arr[0 ~ 2]；
   

3. 第三次遍历数组arr，两两比较arr[i]和arr[i+1]，并将较大者交换到arr[i+1]。第一次遍历前，数组 arr[5] = {1,2,4,5,8}；遍历后，数组arr[5] = {1,2,4,5,8}

4. 第四次遍历数组arr，两两比较arr[i]和arr[i+1]，并将较大者交换到arr[i+1]。第一次遍历前，数组 arr[5] = {1,2,4,5,8}；遍历后，数组arr[5] = {1,2,4,5,8}

5. 第五次遍历数组arr，这次我们只需要遍历 arr[0~0]；也就是只剩下一个元素arr[0]；所以无需比较，产生的数组已经升序有序

代码描述

void bubbleSort(int arr[], int size)
{
	for (int i = 0; i < size; i++) // 可优化点1
	{
		int count = 0;
		for (int j = 0; j < size - i; j++)	// 每次遍历都会产生一个较大值放到后面，所以第i遍历就只需要比较size - i个元素
		{
			if (arr[j] > arr[j+1])//这是升序排法，前一个数和后一个数比较，如果前数大则与后一个数换位置
			{
				int tem = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = tem;
				count = 1;
			}
		}
		if (count == 0) { // 优化点2：如果某一趟没有交换位置，则说明已经排好序，直接退出循环
			break;
		}
	}
}

注释的位置指出了两个优化点
第一个优化点，我们可以修改为 for (int i = 0; i < size - 1; i++)通过上面的图描述，也可以看出实际上n个元素的数组，我们只需要遍历n-1次，第n次遍历时数组只剩下第一个元素“需要”比较，只有一个元素所以可省去多出来的一次循环
第二个优化点，其实已经写出来了，每次遍历比较前，用count记录交换的次数，如果某趟没有发生交换，说明此时数组已经有序，可以直接退出循环
其中，第一个优化点不建议，因为优化跟没优化是一样的，写上size - 1反倒会造成一些误导（因为数组遍历一般都是[0~size)）
第二个优化点可以加上，如果待排序数组是 {1,2,3,5,4}，这样我们只需要执行一次遍历，节省了很多时间