1.HASH函数冲突处理方式不包括以下哪一项

A.开放定址法

B.链地址法

C.插入排序法

D.公共溢出区发

答：C

析：

HASH函数冲突处理方式有：

• 开放定址法：（线性探测再散列，二次探测再散列，伪随机探测再散列）线性探测再散列，就是这个值有冲突就依次加1向下一个寻址直到不冲突为止，但效率偏低 ；所以会使用二次探测再散列，就是使用平方的方式等。
• 再哈希法：就是这个hash函数有冲突，就换一个hash函数试试。
• 链地址法：(Java hashmap就是这么做的）使用链表处理冲突，只要有冲突就增加一个链表节点。
• 建立一个公共溢出区：将哈希表分为基本表和溢出表，凡是有冲突的就直接放到溢出区。

插入排序是排序算法的一种，与哈希无关。

2.下设栈S的初始状态为空，元素a,b,c,d,e,f依次入栈S，出栈的序列为b,d,c,f,e,a，则栈S的容量至少为

A.6

B.5

C.4

D.3

答：D

析：

3.中序遍历二叉排序树可以得到一个从小到大的有序序列。

4.下列选项中，不可能是快速排序第2趟排序结果的是 

A.2,3,5,4,6,7,9

B.2,7,5,6,4,3,9

C.3,2,5,4,7,6,9

D.4,2,3,5,7,6,9

答：C

析：

每经过一趟快排，轴点元素都必然就位，也就是说，一趟下来至少有1个元素在其最终位置。

快排的阶段性排序结果的特点是，第i趟完成时，会有i个以上的数出现在它最终将要出现的位置，即它左边的数都比它小，它右边的数都比它大。

题目问第二趟排序的结果，即要找不存在2个这样的数的选项。A选项中2、3、6、7、9均符合，所以A排除；B选项中，2、9均符合，所以B排除；D选项中5、9均符合，所以D选项排除；最后看C选项，只有9一个数符合，所以C不可能是快速排序第二趟的结果。

5.若一棵二叉树具有12个度为2的节点，6个度为1的节点，则度为0的节点个数是

A.11

B.10

C.13

D.不确定

答：C

析：

由于N=N0+N1+N2，N=2*N2+N1+1，推出N0=N2+1，即叶子节点个数=度为2结点个数+1。

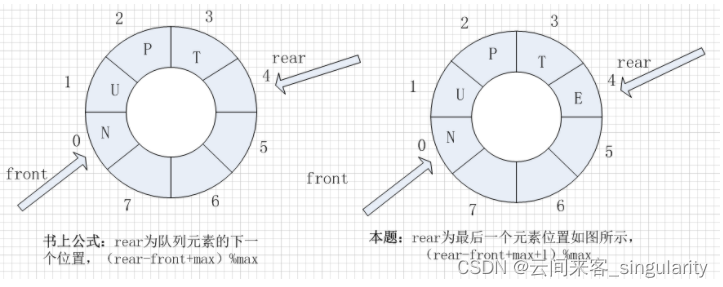
6.大小为MAX的循环队列中，f为当前队头元素位置，r为当前队尾元素位置（最后一个元素的位置），则任意时刻，队列中的元素个数为

A.r-f

B.(r-f+MAX+1)%MAX

C.r-f+1

D.(r-f+MAX)%MAX

答：B

析：

书上公式：(r-f+MAX)%MAX，r指向队尾元素的下一个位置。

本题公式：(r-f+MAX+1)%MAX，r指向队尾元素的位置。

通常最后一个元素不存东西，方便判断队列空还是满。这题是个例外。

 7.已知某个哈希表的n个关键字具有相同的哈希值，如果使用二次探测再散列法将这n个关键字存入哈希表，至少要进行几次探测

A.n-1

B.n

C.n+1

D.n(n+1)

E.n(n+1)/2

F.1+n(n+1)/2

答：E

析：

问的是至少需要多少次探测，即我们假设在上一次探测的基础上，每进行一次二次探测都能直接找到对应的位置。
第一个：直接找到位置，入坑，1次；
第二个：和第一个同hash，找到的位置被第一个给占了，通过二次探测直接找到下一个，入坑，2次；
第三个：第一个被占了，第二个也被占了，通过二次探测直接找到第三个，入坑，3次；
......
第n个：n次；
一共：（1+n）*n / 2 次

注：二次探测属于开放地址法，开放地址法（除了随机探测）都是（1+n）*n / 2 次。

8.已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，最后的叶子节点为

A.34

B.21

C.16

D.12

答：C

析：

将堆画成完全二叉树的形式，堆删除堆顶元素后，是将二叉树最后的叶子节点12放到堆顶，然后将12与其子节点15和10相比较，当15>12时，堆顶12不动，将12与10判断，12>10，不符合小根堆，所以将10和12对调，然后还要将12与其子节点16比较。 所以总共比较3次，最后的叶子节点为16。

 为什么将最后的叶子节点和删除的根节点换？
因为移除根节点后，树就不再是完整的了，数组（这里考虑的是用数组实现堆）中就会有一个空的数据单元，可以把数组中所有的数据都向前移动一个单元，但是这种方法比较慢，所以考虑用最后一个节点填补空的单元，再向下筛选。

9.堆排序平均执行的时间复杂度和需要附加的存储空间复杂度分别是

A.O(n^2)和O(1)

B.O(nlog(n))和O(1)

C.O(nlog(n))和O(n)

D.O(n^2)和O(n)

答：B

析：堆排序的时间复杂度为O(nlog(n))，与树结构有关；空间复杂度为O(1)，只在原数组上操作。

10.将N条长度均为M的有序链表进行合并，合并以后的链表也保持有序，时间复杂度为

A.O(N * M * logN)

B.O(N*M)

C.O(N)

D.O(M)

答：A

析：

方法1：

1. 在每一个链表中取出第一个值，然后把它们放在一个大小为N的数组里，然后把这个数组当成heap建成小(大)根堆。此步骤的时间复杂度为O(N)。

2. 取出堆中的最小值(也是数组的第一个值), 然后把该最小值所处的链表的下一个值放在数组的第一个位置。如果链表中有一个已经为空（元素已经都被取出），则改变heap的大小。此步骤的时间复杂度为O(lg N)。

3. 不断的重复步骤二，直到所有的链表都为空。

建堆只建一次，复杂度为O(N)；调整堆MN-1次，复杂度为(MN-1)*O(lg N)。所以为O(MN*lg N)。

在堆排序中也是一样的，总共n个数，需要得到n个有序的数，那么构建堆需要O(n)，重建堆需要（n-1)*O(lgn)，所以总共复杂度O(nlgn)；如果我只需要前面k个数有序的，那么重构堆需要k*O(lgn)，那么总共复杂度就是O(klgn)

方法2:
m*n个数归并排序复杂度是O(m*nlog(m*n))，即O(m*nlogm)+O(m*nlogn). n个m长度的序列已经是有序的了，每个m长度的序列进行归并排序的时间复杂度为O(mlogm)，则n个m长度的序列的时间复杂度为n*O(mlogm)，前后相减O(m*nlogm)+O(m*nlogn)-n*O(mlogm)=O(m*nlogn)即为答案。
（这里可以看成对n个区间进行归并排序，而每个区间的排序都是独立的）。

方法3:
代入 N=1，不需要排序，凡是非常数的都是错误答案。排除BD
代入 M=1，类似正常排序，NlogN