0 前言
查找算法有4种:
-
线性查找
-
二分查找/折半查找
-
插值查找
-
斐波那契查找
1 线性查找
思路:线性遍历数组元素,与目标值比较,相同则返回下标
/**
*
* @param arr 给定数组
* @param value 目标元素值
* @return 返回目标元素的下标,没找到返回-1
*/
public static int search(int[] arr, int value) {
int index = -1;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value) {
index = i;
}
}
return index;
}
2 二分查找
思路:
-
在第一版search01中编写递归方法:
递归三要素:①传参为目标数组(有序),查找区间的上下界,目标值,返回值为找到的下标 + ②终止条件为区间终止就是目标值(下界>上界表示找不到,则目标值为-1) + ③递归调用为改变区间上界或下界,即向查找区间的左半部分或右半部分查找
-
在第二版search02中:
对search01方法优化:解决了存在多个相同查找目标的问题,当找到目标后并未立即返回,而是向两侧搜索相同值并存放在结果集合中,最后返回结果集
-
在第三版search03中:
采用暴力搜索,将所有目标值的下标收集到集合中
-
对比总结:
第二版和第三版一样是递归但是原理不同,第二版要求数组本身有序所以可以采用if-else结构来递归调用(可以理解为剪枝,即优化),而第三版就是简单的二叉树模型,遍历所有节点去查找目标值
//返回下标,没找到返回-1,前提是数组本身有序
public static int search01(int[] arr,int lo,int hi, int value) {
int index = -1;
//这里为什么不能是大于或等于,因为最后区间大小就是1,即lo==mid==hi
//而任一树枝上(本题只有一只树枝)一定先满足lo==hi(如果能找到此层就该返回正确值),而后才是lo>hi,
if (lo > hi) {
return index;
}
int mid = (lo + hi) / 2;
int midVal = arr[mid];
if (value < midVal) {
index=search01(arr, lo, mid - 1, value);
} else if (value > midVal) {
index=search01(arr, mid + 1, hi, value);
} else {
index=mid;
}
return index;
}
//返回多个相同值的索引集合,前提是数组本身有序
//原理:找到一个正确值后没有立即返回,而是向两侧搜索相同值
public static List<Integer> search02(int[] arr,int lo,int hi, int value) {
ArrayList<Integer> result = new ArrayList<>();
//这里为什么不能是大于或等于,因为最后区间大小就是1,即lo==mid==hi
//而任一树枝上(本题只有一只树枝)一定先满足lo==hi(如果能找到此层就该返回正确值),而后才是lo>hi,
if (lo > hi) {
return result;
}
int mid = (lo + hi) / 2;
int midVal = arr[mid];
if (value < midVal) {
return search02(arr, lo, mid - 1, value);
} else if (value > midVal) {
return search02(arr, mid + 1, hi, value);
} else {
result.add(mid);
int l = mid;
int r = mid;
//注意这里的或不能用短路或,否则后面的r自增不会执行,导致mid重复收集
while (arr[--l] == midVal | arr[++r] == midVal) {
if (arr[l] == midVal) {
result.add(l);
}
if (arr[r] == midVal) {
result.add(r);
}
}
}
return result;
}
public static List<Integer> list = new ArrayList<>();
//基于search01优化:返回若干个相同值
//不同于search01,方法1的原理是树只有一个树枝,遇到正确结果立即层层返回
//search03原理,没有返回值,暴力搜索,遍历多个树枝的所有节点,收集所有满足的结果放入全局变量list集合
//当然本方法不要求数组本身有序
public static void search03(int[] arr,int lo,int hi, int value) {
//这里为什么不能是大于或等于,因为最后区间大小就是1,即lo==mid==hi
//而任一树枝上(本题只有一只树枝)一定先满足lo==hi(如果能找到此层就该返回正确值),而后才是lo>hi,
if (lo > hi) {
return;
}
int mid = (lo + hi) / 2;
int midVal = arr[mid];
if (value == midVal) {
list.add(mid);
}
search03(arr, lo, mid - 1, value);
search03(arr, mid + 1, hi, value);
}
3 插值查找
引出:二分查找简单说就是看中间,不停地对半砍同时看正中间是不是我要的,那么问题就来了,如果我要的就是最左边,那得切多少下才能切到最左边,简单!不要对半切就行了,改下权重就解决
思路:将权重由1/2改为自适应,在数据量较大且分布均匀时明显效率更优,不再对半切了,你要的值和两边中哪边差不多就往那边切,找起来快多了
//基于二分查找的改良,将权重由1/2改为自适应,在数据量较大且分布均匀时明显效率更优
public static int search01(int[] arr,int lo,int hi, int value) {
int index = -1;
//优化:查找值超过极值则直接返回-1
if (lo > hi||value<arr[0]||value>arr[arr.length-1]) {
return index;
}
//(value-arr[lo])/(arr[hi]-arr[lo])就是自适应的权重,二分的权重是1/2
int mid = lo+(hi-lo)*( (value-arr[lo])/(arr[hi]-arr[lo]) );
int midVal = arr[mid];
if (value < midVal) {
index=search01(arr, lo, mid - 1, value);
} else if (value > midVal) {
index=search01(arr, mid + 1, hi, value);
} else {
index=mid;
}
return index;
}
4 斐波那契查找
引出:如果说二分找中间快,插值找两边快(中间也快),那么斐波那契查找就是鸡肋中的鸡肋,华而不实的lj东西
思路:首先你得拿到著名的斐波那契数列(1,1,2,3,5,8…),假定给定的待排序数组arr大小为6,那么给它扩到斐波那契数列的下一级,6和5一级,下一级就是8,扩充的元素就是当前的最后一个元素,完事就开始砍,不是对半砍,你得找到可以砍的地方,满足砍完左右两部分的数组大小刚好在斐波那契数列中,比如8个元素,对着arr[4]砍一刀,左边包含arr[0]到arr[4]即大小为5的数组,右边就剩下标为567了,砍的同时看下刀点arr[4]是不是你要的,整体就是这样一直砍一直看下刀点
总结:且不说这种砍法没有实际意义,说白了就是二分查找的权重改为无限接近黄金分割比0.618(而且数组越大越接近0.618,数组越小越接近1),那你干嘛不直接用0.618呢,况且你砍完之后,下刀点那个元素还是归到了左半部分,这就太sb了,完全就是为了凑数组大小为斐波那契数列中的元素值了,造成重复判断
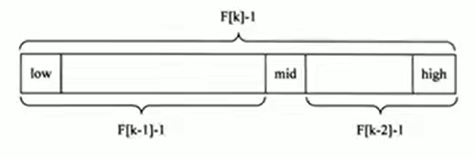
//获取斐波那契数组方法
public static int[] fib() {
int[] f = new int[20];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < 20; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//查找方法,不使用递归实现
//斐波那契查找说到底只是让查找的区间大小一直在斐波那契数列中
//,说白了就是切割比接近0.618,既然如此为什么不将二分查找的逻辑改为权重0.618
//,纯粹就是装杯吧,说是感受数学之美还比不上插值查找的自适应权重有用
public static int search(int[] arr, int value) {
int lo = 0;
int hi = arr.length - 1;
int key = 0;//指针指向斐波那契数列元素,用以控制区间大小
int mid = 0;//切割点
int[] f = fib();//斐波那契数列
//临时数组扩容到原数组大小的下一级,比如6扩容到5的下一级8
while (hi > f[++key]-1) {
}
int[] temp = Arrays.copyOf(arr, f[key]);
for (int i = hi+1; i < temp.length; i++) {
temp[i] = temp[hi];
}
//此时key==5,f[key]==8,f[key-1]==5,f[key-2]==3,lo==0,hi==5,temp.length==8,mid==4
//主要就是保证lo和hi的差值就是斐波那契数列的某个值-1,即查找的区间大小就是斐波那契数列值
//缩小查找区间只需使key自减就行,但是
//上下界的变迁需要注意,hi变迁只需赋为mid,lo却赋为mid+1,这是因为mid和hi间距是f[key-2]需要-1
while (lo < hi) {
mid = lo+ f[key - 1] - 1;
if (value < temp[mid]) {
hi = mid;
key--;
} else if (value > temp[mid]) {
lo = mid + 1;
key -= 2;
} else {
return mid;
}
}
//hi==lo+f[k]-1,f[k]>=1
if (lo == hi) {
return lo;
}
return -1;
}