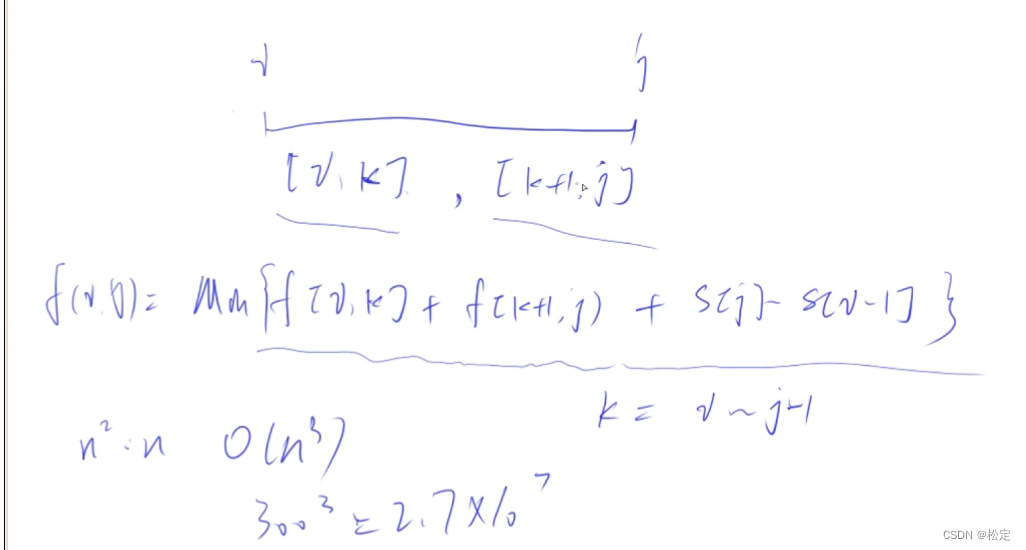思路：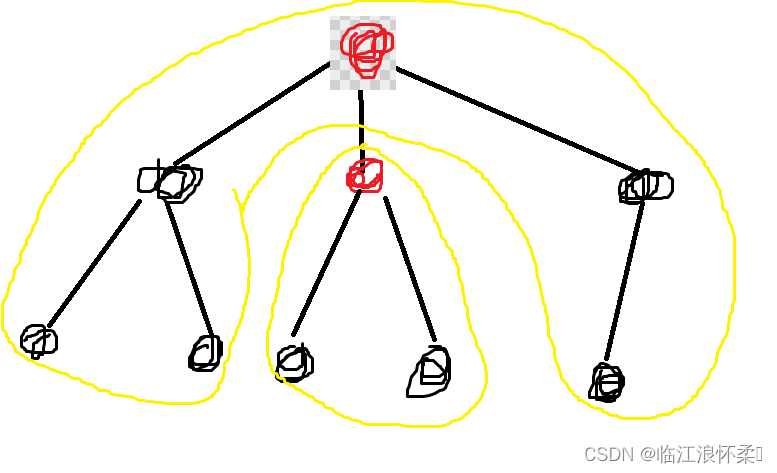

因为如果红色节点的子树中如果有红色节点的话，那么该子树对其不会造成影响，不用考虑，因此我们在考虑每个红色节点时，不考虑其红色子树。那么如图，对每个红色节点答案有贡献的就是其所有非红色子节点的权值和。我们用dfs处理出每个红点的非红节点子树，然后枚举每个红色节点，然后在枚举该红色节点包括的所有结点中1的个数，保证1的个数不会超过2个，其他的结点权值为2.

代码：

int n;
string s;
vector<int>e[1000010], vc[1000010];
int ans[1000010];

void dfs(int now,int md){
    vc[md].push_back(now);
    for(auto y : e[now]){
        if(s[y] == 'R')
            dfs(y, y);
        else
            dfs(y,md);
    }
}


void solve(){
    cin >> n;
    cin >> s;
    s = " " + s;
    for(int i = 2;i <= n;i ++){
        int x;
        cin >> x;
        e[x].push_back(i);
    }
    dfs(1,1);
    bool f = false;
    for(int i = 1;i <= n;i ++)ans[i] = 1;
    for(int i = 1;i <= n;i ++){
        if(s[i] != 'R')continue;
        int sz = vc[i].size();
        bool ok = false;
        for(int j = 0;j < 3;j ++){
            if(j > sz){
                break;
            }
            if((j + (sz - j) * 2) % 3 == 0){
                ok = true;
                for(int k = 0;k < j;k ++)ans[vc[i][k]] = 1;
                for(int k = j;k < sz;k ++)ans[vc[i][k]] = 2;
                break;
            }
        }
        if(!ok){
            f = true;
            break;
        }
    }
    if(f)
        cout << -1 << endl;
    else
        for(int i = 1;i <= n;i ++)
            cout << ans[i];
}