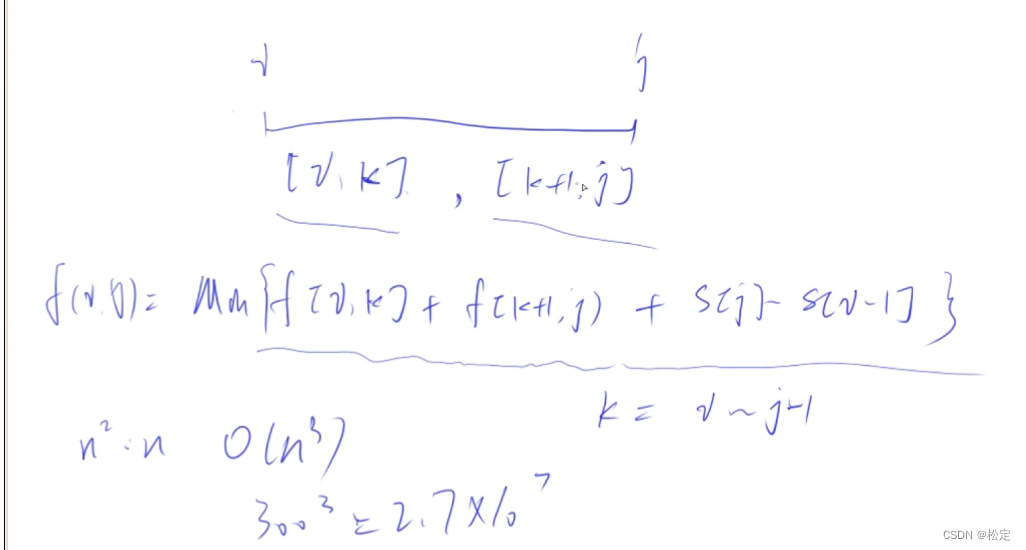
根据题意要求的是将石子合并的最小权值，我们可以根据DP思想使用二维数组f[i,j]来存放所有从第i堆石子到第j堆石子合并成一堆石子的合并方式。

然后由第二个图所示，我们可以将i到j区间分成两个区间，因为将i到j合并成一个区间的前一步一定是合并前两个区间。因此我们可以将状态计算的递归定义为区间的中间，通过变化区间的中间来寻找合并i到j的最小值。

也就是f[i,j]=min(f[i,k]+f[k+1,j]+s[j]-s[i-1]

例题：https://www.acwing.com/problem/content/284/ 

#include<iostream>
using namespace std;

const int N=310;
int n;
int f[N][N];
int s[N];

int main()
{
    cin>>n;
    int a;
    for(int i=1;i<=n;i++) //前缀和
    {
        scanf("%d",&a);
        s[i]=s[i-1]+a;
    }
    
    
    for(int len=2;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int l=i ,r=i+len-1;
            f[l][r]=1e8;
            for(int k=l;k<r;k++)
            {
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }
        }
    }
    
    cout<<f[1][n];
    return 0;
}

k的取值范围:

这里划分出的区间是[l, k], [k+1, r]

说明： [l, l] [r, r] 这两个区间都是不为空的，至少包含了一堆石子。

前提：划分出的两个区间都不为空的情况下，讨论k的取值范围

所以，对于[l, k] k可以取到 l 对于[k+1, r] ， 因为k+1 <= r, 所以 k <= r - 1, 即 k < r