C2-1.6 Dropout正则化——提高泛化能力

1、参考书籍

2、什么是Dropout正则化

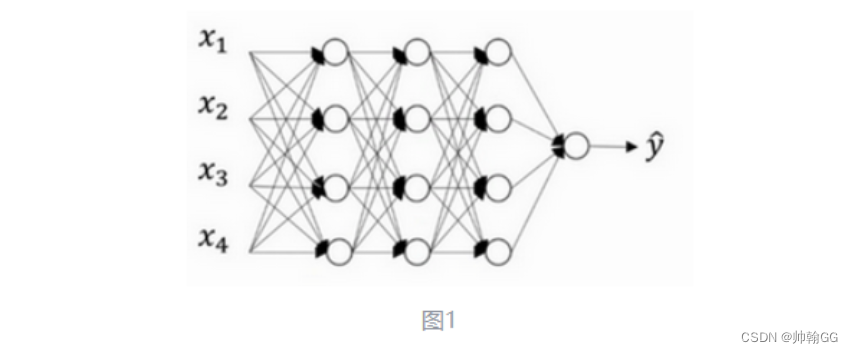
以图一为例：

• 假设在训练图一所示的神经网络，它存在过拟合（模型过于复杂情况），dropout 会遍历网络的每一层（每一层设置的阈值不同），并随机消除神经网络中一些节点。假设每个节点得以保留和消除的概率都是0.5。设置完节点概率会消除一些节点，然后删除掉从该节点进出的连线，

• 目的：随机消除一些神经元，让网络规模更小，模型变得相对简单一些。

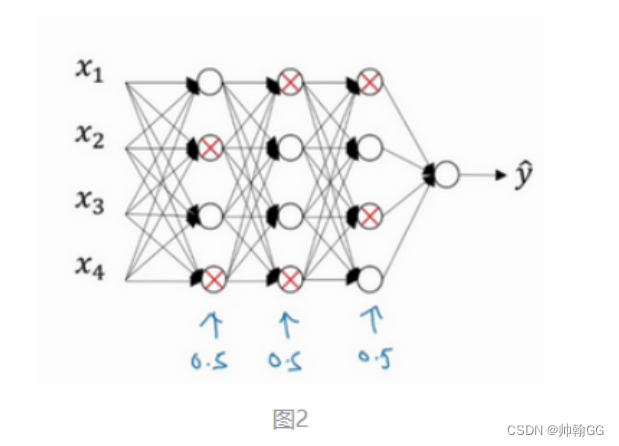
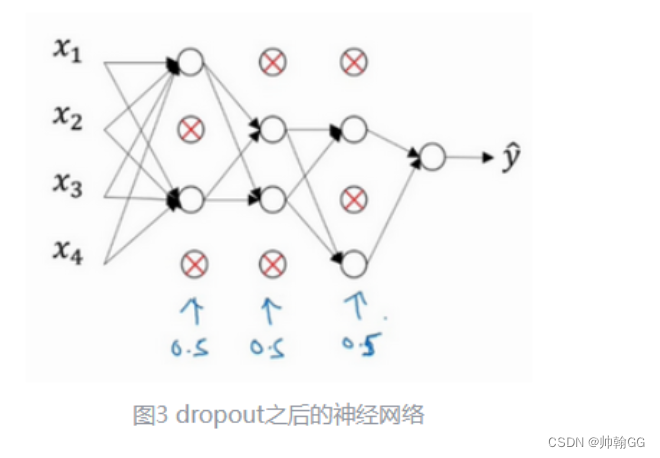
3、大致经历了如下三个过程：反向随机失活法

以第三层隐藏层为例：

步骤一：创建一个与a[3]（从后向前的）相同形状的 分布，数值在[0,1]中间的 随机矩阵d[3]

代码如下：

d3 = np.random.rand(a3.shape[0], a3.shape[1])

• np.random.rand(x, y) 生成一个形状为 (x, y) 的矩阵，其中的元素是从 [0, 1) 区间内均匀分布的随机数。
• a3.shape[0] 表示a3的行数
• a3.shape[1] 表示a3的列数

步骤二：通过 d3 < 0.8（阈值自己设定，这里自己设定是0.8） 创建一个布尔矩阵

• 单元的概率此处等于0.8，它意味着消除任意一个隐藏单元的概率是0.2，保留下来的概率是0.8

• 其中小于 0.8 的元素为 True（表示这些神经元将被失活），其余为 False。

• d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep.prob

• 所有小于keep.prob的都置为0，其余置1.

代码如下：

d3 = d3 < 0.8

步骤三：获取随机失活后的a[3]的激活函数

• 代码如下：

a3 = np. multipy (a3，d3)

这里a3 d3对应位置相乘，a3是原来神经网络中第三层隐藏层的激活函数，d3是 0-1与a3分布相同的矩阵，里面的数据是True / False。

相乘后的结果：

• np.multiply()方法得到的结果是两个数组进行对应位置的乘积

第一个数组：
[[0. 1. 2.]
 [3. 4. 5.]
 [6. 7. 8.]]


第二个数组：
[10 10 10]

print ('两个数组相乘：')
print (np.multiply(a,b))


两个数组相乘：
[[ 0. 10. 20.]
 [30. 40. 50.]
 [60. 70. 80.]]

※步骤四（改进后的）：

​ 假设第三隐藏层上有 50个单元或50个神经元在一维上是通过因分解拆分成50 x m 维的保留和删除它们的概率分别为 80%和20%。这意味着最后被删除或归零的单元平均有10(50x20% =10)个z[4] = w[4] * a[3] + b4，预期是减少20%，也是说a[3]中有20%的元素被归零，为了不影响Z[4]的期望值，需要用w4/0.8它将修正或弥补所需的那20%，这样a[3]的期望值不会变，

4、对步骤四的理解：

问题疑惑：

在解释为什么在使用反向随机失活（Inverted Dropout）时不对激活值的减少进行调整会导致训练和测试时网络行为不一致之前

好的，我将尝试用一个更简单的比喻来解释这个概念。

想象一下，你在训练一个运动队。在训练时，为了增强队员们的适应能力，你决定让他们轮流休息，每次只有部分队员参与训练。这相当于在神经网络训练中应用 Dropout：每次训练只有部分神经元是激活的。

现在，如果在训练时，你的队伍因为队员轮休而总是以较低的强度训练，那么他们可能会习惯于这种低强度的训练。但是，在真正的比赛（相当于神经网络的测试阶段）中，所有队员都需要上场，此时比赛的强度会比训练时高得多。如果队伍没有在训练时准备好应对全员参与的高强度比赛，他们可能在真正的比赛中表现不佳。

在神经网络的情况中，"强度"可以类比为激活值的总和。在使用 Dropout 的训练过程中，由于一些神经元被随机关闭，激活值的总和会减少。如果我们不对这种减少进行调整，网络可能会适应这种低激活值的状态。但是，在测试阶段，当所有神经元都激活时（即没有应用 Dropout），激活值的总和会增加，这可能导致网络在处理真实数据时的表现与训练时有很大差异。

因此，在反向随机失活中，我们在训练阶段对激活值进行放大，以模拟测试阶段所有神经元都激活的情况。这样做的目的是为了使网络在训练和测试时面对相似的条件，从而改善其在处理新数据时的泛化能力和性能。

5、 对Dropout的自我理解纠正过程

※※※When you shut some neurons down, you actually modify your model. The idea behind drop-out is that at each iteration, you train a different model that uses only a subset of your neurons. With dropout, your neurons thus become less sensitive to the activation of one other specific neuron, because that other neuron might be shut down at any time.

就是说，在训练过程中，随机失活是暂时的，真正应用的时候所有的激活函数都是激活状态。而不是我以前的理解：把复杂的神经网络变成简化的神经网络，然后就一直这样了

1、训练阶段的随机失活：

• 在训练过程中，随机关闭一部分神经元是一种防止网络过拟合的策略。这个过程是动态的，意味着在每次训练迭代中，被关闭的神经元都是随机选取的。
• 这种方法可以防止网络过度依赖训练数据中的特定模式，从而增强模型对新数据的泛化能力。

2、测试阶段的全激活状态：

• 在测试或实际应用阶段，所有的神经元都是激活的。也就是说，不再应用 Dropout，网络以其完整的形式运作。
• 这是因为在测试时，我们希望网络能够利用其所有学到的特征和模式来做出最佳判断。

3、Dropout 的目的和误解：

• Dropout 的目的不是将复杂的网络变成一个简化的版本，然后一直保持这种简化状态。
• 相反，它的目的是在训练过程中增加一种随机性，迫使网络学习更加鲁棒（即：less sensitive）的特征表示。这样，网络不会对训练数据中的任何特定小组件过度敏感。

实现过程的视频：

C:\Users\Administrator\Documents\WeChat Files\wxid_99i8u6vcmh1m22\FileStorage\Video\2023-12\683aaebc9ef05d6352e1a352f0c71212.mp4

6、对Dropout进行过拟合归为三大分类的一类：

解决过拟合大概分为3个类别：1、数据集不足。2、输入特征过多，影响了正常的X与Y之间的映射。3、模型过于复杂。 那Dropout属于哪一类呢？？

答：Dropout 正则化主要针对的是第三类问题：模型过于复杂。

在深度学习中，过拟合通常发生在**模型太复杂时，**这意味着模型有太多的参数，可以学习训练数据中的每一个小细节，包括噪声和不重要的特征。这导致模型在新数据上的表现不佳，因为它过度适应了训练数据。

**Dropout 通过在训练过程中随机“关闭”一些神经元，来减少模型的复杂性。**这样做的效果相当于是在每次迭代中使用一个更简单的网络版本。**这种随机性迫使网络不能依赖于任何单一的特征或神经元组合，**因此它必须学习更加广泛和鲁棒的特征表示。结果就是，Dropout 可以减少模型的过拟合，提高其在新、未见数据上的表现。

总结来说，Dropout 是解决模型过于复杂导致的过拟合问题的一种方法。它通过在训练期间引入随机性来降低模型的有效复杂度，从而提高其泛化能力。

6、Dropout的理解 / 原理

6.1 【书籍参考】

6.2 Dropout的本质：

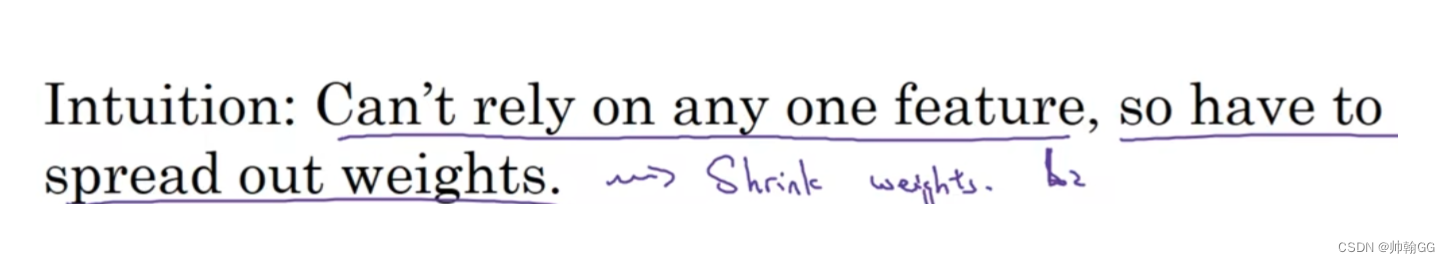
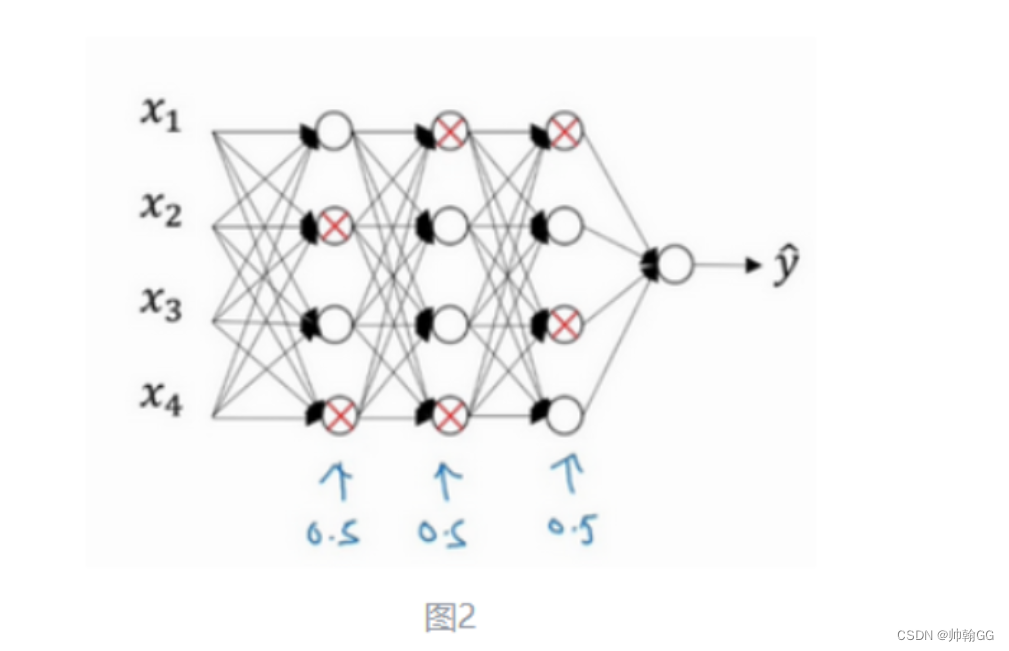
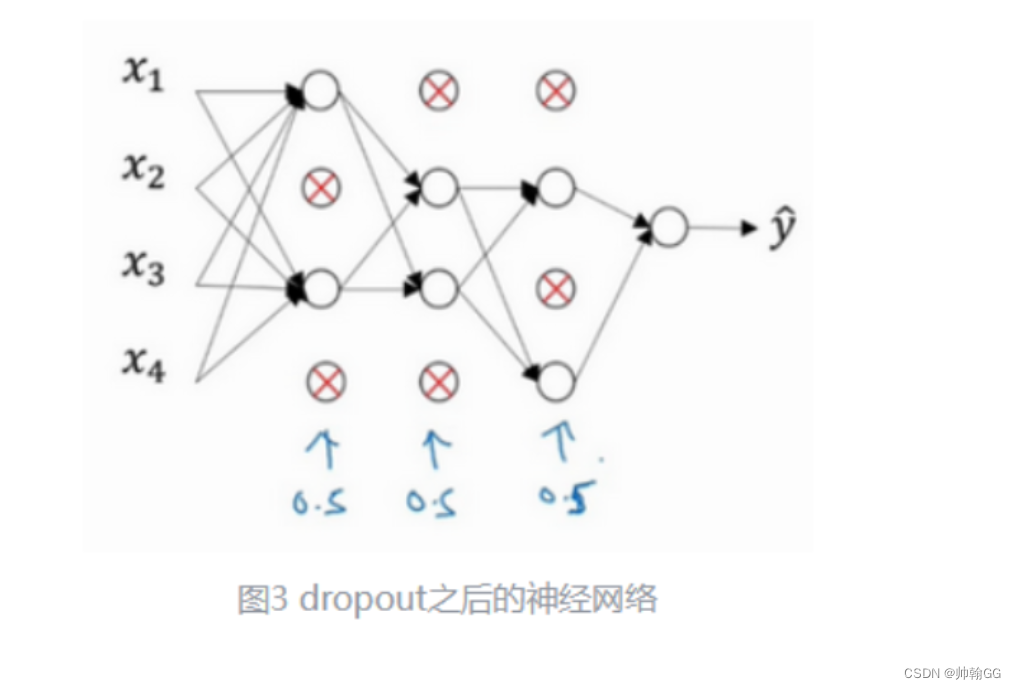
以下图为例：

• “不能依赖于任何一个特征，不得不将权重进行分散”

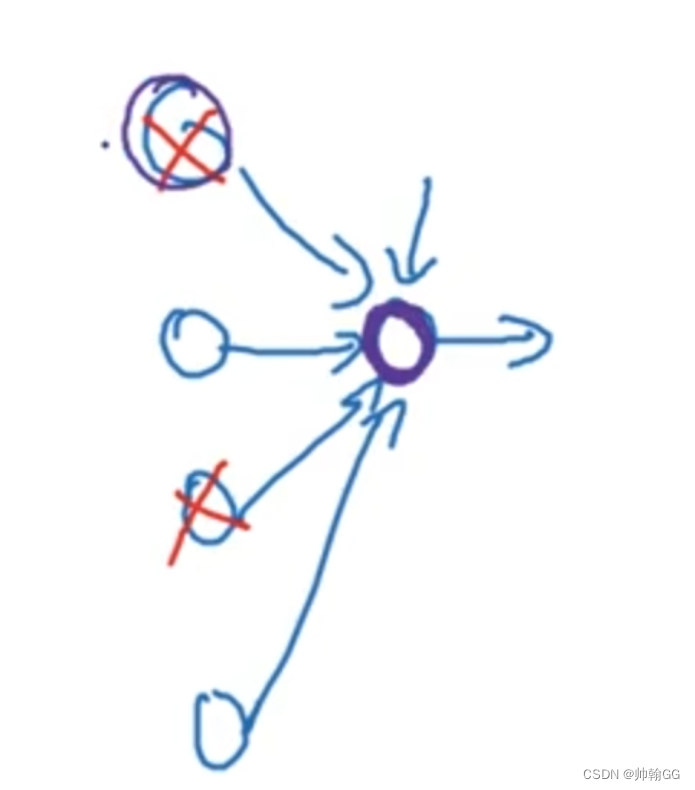
• ​ 这里有四个输入单元 /某一个隐藏层的四个神经单元，因为通过Dropout的随机失活，每一个特征 （神经元）都有可能被随机清除。

• ※※所以，类似于“不要把鸡蛋放在一个篮子里”，由于Dropout的使用，不要把所有的赌注都放在一个点上（不要让某一个特征所占权重特别大），也不要给任何一个输入加上太多权重。

• ※Dropout与L2正则化类似：

  • **L2正则化：**对不同函数的衰减是不同的，这个取决于 激活函数权重的大小。
  • **Dropout正则化：**根据权重W来判断每一层神经网络神经元的个数，根据得出的个数，来手动设定每一层保留单元的概率。所以不同层的保留单元的概率是不同的。（某一层神经元个数多，设置的阈值就小一点，保留的少一点。。。某一层神经元个数少，设置的阈值就大一点，甚至可以是1，保留的多一点 ）

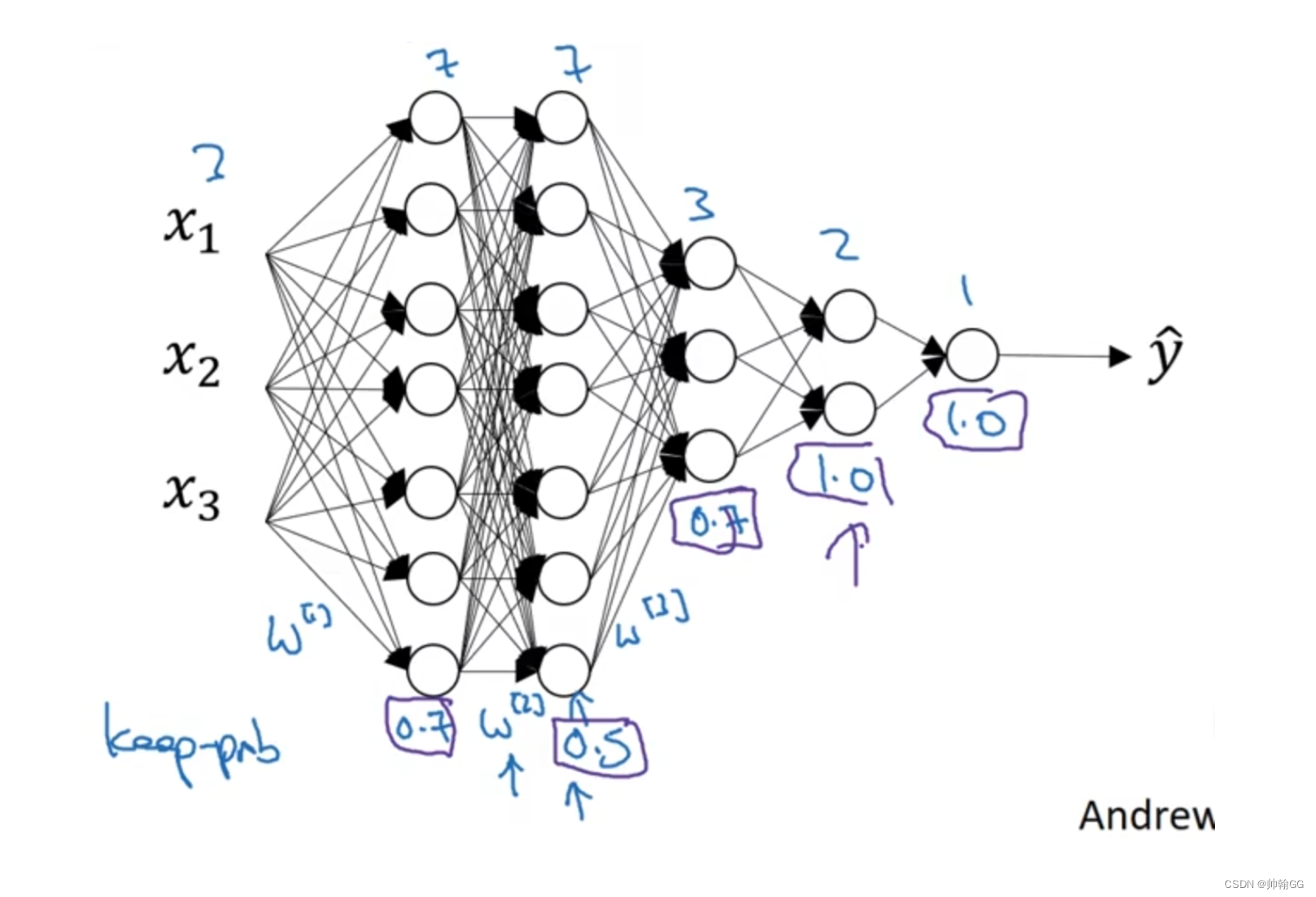
6.3 Dropout过程举例

• **解释一下为什么这里要通过W权重矩阵，再进行设置keep-prob：**因为我们不能像视频展示的可视化神经网络以及每一层隐藏层的神经元个数，所以通过W矩阵来进行判断每一层隐藏层的神经元个数大小
• 实施dropout 要选择的参数代表每一层上保留单元的概率。所以不同层的保留概率也可以变化。**第一层，矩阵 w1是（7，3）第二个权重矩阵w2（7,7）第三个权重矩阵w3（3,7）**以此类推。w2是最大的权重阵，因为w2拥有最大参数集，即7x7，为了预防矩阵的过拟合，对于这一层，它选的值应该相对较低假设是0.5。对于其他层，过拟合的程度可能没那么严重，它们的值可能高一些。