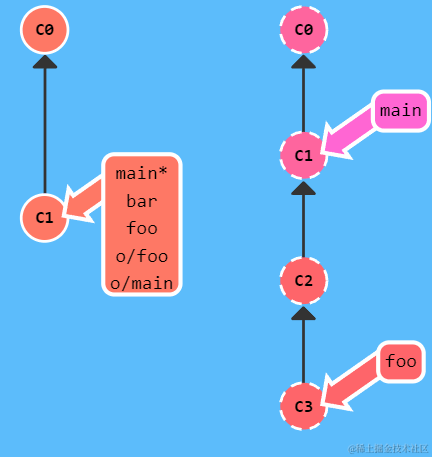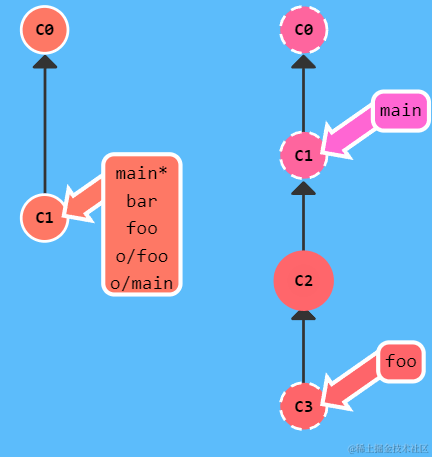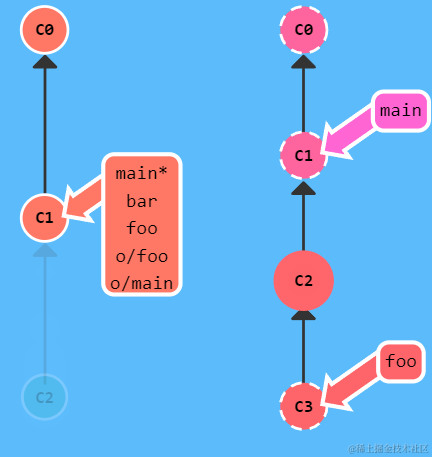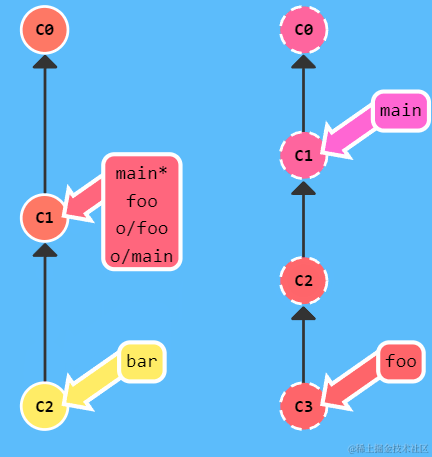
排序贪心
区间贪心
删数贪心
统计二进制下有多少1
int Getbit_1(int n){
int cnt=0;
while(n){
n=n&(n-1);cnt++;
}
return cnt;
}
暴力加一维前缀和优化
#include <iostream>
#include <climits>
using namespace std;
#define int long long
const int N=2e5+10;
int a[N],sum[N];
signed main(){
int n,mx=INT_MIN;cin>>n;
//先求前缀和
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]+a[i];
}
for(int l=1;l<=n;l++){
for(int r=l;r<=n;r++){
// l r 就是区间-->前缀和
int sum_l_r=sum[r]-sum[l-1];
mx=max(mx,sum_l_r);
}
}
cout<<mx<<endl;
return 0;
}
贪心 sum<零 清零
#include <iostream>
#include <climits>
using namespace std;
#define int long long
const int N=2e5+10;
signed main(){
int n,mx=INT_MIN,sum=0;cin>>n;
for(int i=1;i<=n;i++){
int x;cin>>x;
if(sum<0) sum=0;
sum+=x;
mx=max(mx,sum);
}
cout<<mx<<endl;
return 0;
}
#include <iostream>
#include <climits>
using namespace std;
#define int long long
const int N=1e2+10;
int a[N][N];
signed main(){
int n;cin>>n;
//固定左上角 枚举右下脚
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
}
}
//枚举
int mx=INT_MIN;
for(int i1=1;i1<=n;i1++){
for(int j1=1;j1<=n;j1++){
for(int i2=i1;i2<=n;i2++){
for(int j2=j1;j2<=n;j2++){
//i1 j1 i2 j2
int sum=0;
for(int i=i1;i<=i2;i++){
for(int j=j1;j<=j2;j++){
sum+=a[i][j];
}
}
mx=max(mx,sum);
}
}
}
}
cout<<mx<<endl;
return 0;
}
一维前缀和 求二位区间和
#include <iostream>
#include <climits>
using namespace std;
#define int long long
const int N=1e2+10;
int a[N][N],presum[N][N];
signed main(){
int n;cin>>n;
//固定左上角 枚举右下脚
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
presum[i][j]=presum[i][j-1]+a[i][j];
}
}
/*
* 1 2 3 4 5
* 6 7 8 9 1
* 2 3 2 4 1
* 3 3 2 1 1
* */
//枚举
int mx=INT_MIN;
for(int i1=1;i1<=n;i1++){
for(int j1=1;j1<=n;j1++){
for(int i2=i1;i2<=n;i2++){
for(int j2=j1;j2<=n;j2++){
int sum=0;
for(int i=i1;i<=i2;i++){
sum+=presum[i][j2]-presum[i][j1-1];
}
mx=max(mx,sum);
}
}
}
}
cout<<mx<<endl;
return 0;
}

二维前缀和求区间和
#include <iostream>
#include <climits>
using namespace std;
#define int long long
const int N=1e2+10;
int a[N][N],presum[N][N];
/*
* 遇到一维数组求最大连续子数组和 以及二维数组求最大连续子数字和问题
* 都可以通过暴力枚举区间来找到最大值
* 一、一维数组
* 1.对于一维数组,暴力枚举区间需要两层循环,l r
* 2.求l r 区间内的和可以预先输入的时候存储区间和,然后通过区间和求前缀和
* 二、二位数组
* 1.对于二位数组来说,暴力枚举区间需要四层循环,就是左上角左边(i1,j1),右下角坐标(i2,j2)
* 2.对(i1,j1) (i2,j2)求区间和比较复杂,还是输入的时候前缀区间和,
* 3.二维区间和:sum=presum[i2][j2]-presum[i1-1][j2]-presum[i2][j1-1]+presum[i1-1][j1-1]
* 4.二维求前缀和的时候,需要画图,presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+a[i][j];
* */
signed main(){
int n;cin>>n;
//固定左上角 枚举右下脚
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+a[i][j];
}
}
/*
* 1 2 3 4 5
* 6 7 8 9 1
* 2 3 2 4 1
* 3 3 2 1 1
* */
//枚举
int mx=INT_MIN;
for(int i1=1;i1<=n;i1++){
for(int j1=1;j1<=n;j1++){
for(int i2=i1;i2<=n;i2++){
for(int j2=j1;j2<=n;j2++){
int sum=presum[i2][j2]-presum[i1-1][j2]-presum[i2][j1-1]+presum[i1-1][j1-1];
mx=max(mx,sum);
}
}
}
}
cout<<mx<<endl;
return 0;
}