目录
一,3042. 统计前后缀下标对 I
二,3043. 最长公共前缀的长度
三,3044. 出现频率最高的质数
四,3045. 统计前后缀下标对 II
一,3042. 统计前后缀下标对 I

该题数据范围小,可直接暴力求解, 代码如下:
class Solution {
public int countPrefixSuffixPairs(String[] words) {
int n = words.length;
int ans = 0;
for(int i=0; i<n; i++){
String s1 = words[i];
for(int j=i+1; j<n; j++){
String s2 = words[j];
if(s2.startsWith(s1) && s2.endsWith(s1))
ans++;
}
}
return ans;
}
}二,3043. 最长公共前缀的长度
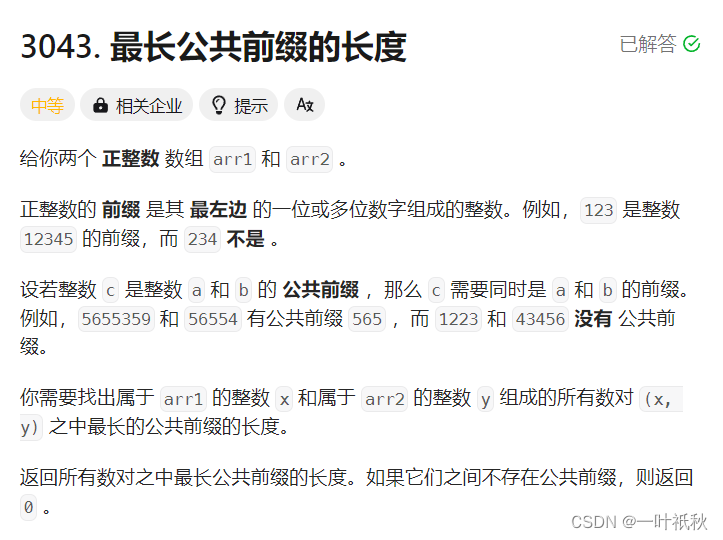
该题是求两个数组最大前缀的长度,可以直接使用Hash来存储数组arr1的所有前缀,再遍历数组arr2 来看在arr1中(即hash表)是否有匹配的前缀, 最后通过额外的变量来求这些匹配字符串的最大长度。
代码如下:
class Solution {
public int longestCommonPrefix(int[] arr1, int[] arr2) {
Set<String> set = new HashSet<>();
for(int x : arr1){
String t = String.valueOf(x);
for(int i=1; i<=t.length(); i++)
set.add(t.substring(0,i));
}
int ans = 0;
for(int x : arr2){
String t = String.valueOf(x);
for(int i=1; i<=t.length(); i++)
if(set.contains(t.substring(0,i)))
ans = Math.max(ans, i);
}
return ans;
}
}又因为题目中给的数据都是整形,所以我们也可以通过存储数字来匹配,这样可以节省一点时间,代码如下:
class Solution {
public int longestCommonPrefix(int[] arr1, int[] arr2) {
Set<Integer> set = new HashSet<>();
for(int x : arr1){
for(; x>0; x/=10)
set.add(x);
}
int ans = 0;
for(int x : arr2){
for(; x>0; x/=10){
if(set.contains(x)){
ans = Math.max(ans, x);
break;
}
}
}
return ans>0?String.valueOf(ans).length():0;
}
}三,3044. 出现频率最高的质数

本题是一道单纯的模拟题,没什么可讲的,直接上代码:
class Solution {
//定义的各个方向
static int[][] dirt = new int[][]{
{0,1},{0,-1},{1,0},{-1,0},
{1,1},{-1,-1},{-1,1},{1,-1}
};
public int mostFrequentPrime(int[][] mat) {
int n = mat.length;
int m = mat[0].length;
Map<Integer, Integer> map = new HashMap<>();
int mx = 0;
for(int x=0; x<n; x++){
for(int y=0; y<m; y++){
for(int[] d : dirt){
int num = mat[x][y];
for(int dx=x+d[0],dy=y+d[1]; dx>=0&&dx<n&&dy>=0&&dy<m; dx+=d[0],dy+=d[1]){
//已经确保 num > 10
num = num*10 + mat[dx][dy];
if(isPrime(num)){
map.put(num, map.getOrDefault(num,0)+1);
//求质数出现的最大次数
mx = Math.max(mx, map.get(num));
}
}
}
}
}
int ans = 0;
for(Map.Entry<Integer,Integer> x : map.entrySet())
if(x.getValue()==mx){//如果出现次数相同,求其中最大的质数
ans = Math.max(x.getKey(),ans);
}
return ans==0?-1:ans;
}
//是否是质数
boolean isPrime(int x){
for(int i=2; i<=Math.sqrt(x); i++){
if(x%i == 0)
return false;
}
return true;
}
}四,3045. 统计前后缀下标对 II

本题和第一题是一样的,只不过数据范围太大,所以不能暴力,这里写两种写法:
1)z函数 + 字典树
1.1 z函数
- z函数是一种用于求解字符串匹配中最长公共前缀的函数。给定一个字符串 s,z函数值 z[i] 表示以 s[i] 为起始的子串与原字符串 s 的最长公共前缀长度
- 更具体一点:z[i] = max { k | s[ 0,k-1 ] = s[ i,i+k-1 ] }
而在本题当中,我们只要保证 z[ n - i - 1] == i + 1 即 s[n-i-1,n-1] == s[0,i],就可以确定这个字符串 s 的前后缀是相同的,也就是说使用z函数就是为了让我们可以只考虑前缀,那么如何来求公共前缀的个数呢?这时候就用到了字典树。
1.2 字典树
- 又称单词查找树,Trie树,是一种哈希树的变种。是用于统计,排序和保存大量的字符串,但不仅限于字符串。利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,画个图理解一下:
- 当我们知道字典树长什么样以及存储的数据后,可能就会有这样的疑惑,我们要如何使用这颗字典树来求公共前缀呢,再来画个图来理解一下:
代码如下:
class Solution {
static class Node{
Node[] son = new Node[26];
int cnt;
}
public long countPrefixSuffixPairs(String[] words) {
long ans = 0;
Node root = new Node();//前缀字典树
for(String T : words){
char[] t = T.toCharArray();
int n = t.length;
//z函数实现
int[] z = new int[n];
z[0] = n;
int l=0,r=0;
for(int i=1; i<n; i++){
if(i <= r) z[i] = Math.min(z[i-l], r-i+1);
while(i+z[i]<n && t[z[i]] == t[i+z[i]]){
l = i;
r = i+z[i];
z[i]++;
}
}
//字典树实现,边比较边建立字典树
Node cur = root;
for(int i=0; i<n; i++){
if(cur.son[t[i]-'a']==null)
cur.son[t[i]-'a'] = new Node();
cur = cur.son[t[i]-'a'];
if(z[n-1-i] == i+1)//判断前后缀相同
ans += cur.cnt;
}
cur.cnt++;
}
return ans;
}
}2)只使用字典树
比如有两个字符串 s1 = "ab",s2 = "abeab",有没有一种方法可以同时比较前后缀呢?我们可以求出 pair(s[i], s[n-i-1]) 进行比较, 画个图理解一下:
class Solution {
static class Node{
Map<Integer, Node> son = new HashMap<>();
int cnt;
}
public long countPrefixSuffixPairs(String[] words) {
long ans = 0;
Node root = new Node();
for(String T : words){
char[] t = T.toCharArray();
int n = t.length;
Node cur = root;
for(int i=0; i<n; i++){
//数据最大是10^5,使用整数代替 (a,b)
int p = (t[i]-'a')<<5 | (t[n-1-i]-'a');
if(cur.son.getOrDefault(p,null)==null)
cur.son.put(p,new Node());
cur = cur.son.get(p);
ans += cur.cnt;
}
cur.cnt++;
}
return ans;
}
}