图形系统开发实战课程：进阶篇（上）—

图形开发学院｜GraphAnyWhere

课程名称：图形系统开发实战课程：进阶篇(上)
课程章节：“图形交互操作:拾取”
原文地址：https://www.graphanywhere.com/graph/advanced/2-6.html

第六章图形交互操作:拾取

$\quad$ 在图形系统中，拾取是指从屏幕上选择一个图形对象的过程。这个过程通常是通过鼠标或触摸屏等输入设备来实现的。当用户将鼠标移动到图形对象上时，图形系统会检测到鼠标的位置，然后根据鼠标位置计算该位置上的图形对象，从而实现了拾取操作，这个过程也称之为‘碰撞检测’。

$\quad$ 由于 Canvas 不会保存绘制图形的信息，一旦绘制完成用户在浏览器中得到的是一张图片，用户在图片上点击时时不能直接获取到对应的图形对象，所以在绘图时需要缓存已经绘制的图形对象，碰撞检测有以下几种方案：

内置API法：通过Canvas渲染上下文对象内置的 API，实现拾取图形
几何法：通过几何运算，判断鼠标点击位置附近的对象，实现拾取图形
取色法：通过获取点击位置的颜色值，实现图形拾取

1 内置API法

$\quad$ Canvas 渲染上下文对象提供了 isPointInPath() 可以判断一个坐标点是否在路径内, 提供了 isPointInStroke() 判断一个坐标点是否在描边的边上。

$\quad$ 我们在 图形系统开发实战课程-基础篇 中曾经讲述了Canvas路径的用法，路径可完成各种常见基本几何图形，和贝塞尔曲线的绘制，下图是 anyGraph内置的一些点的类型。

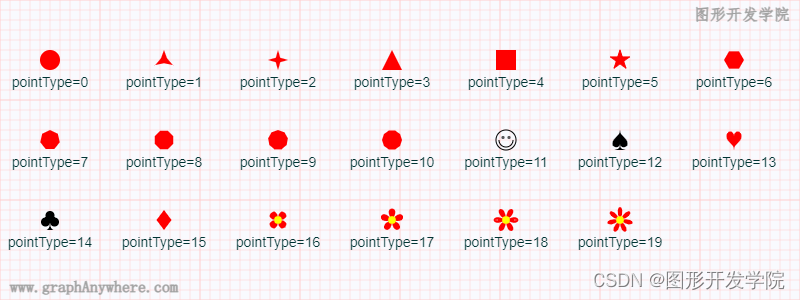
在这里插入图片描述

$\quad$ 上面这些点类型均是通过路径绘制出来的，从这张图可以看出通过路径我们不仅仅可以绘制常见的几何图形，如三角形、矩形、圆形、多边形，还可以绘制诸如黑桃、红桃、梅花、花朵等复杂的带有曲线的图形。

$\quad$ 如今 Canvas 渲染上下文对象更是提供了 isPointInPath() 可以判断一个坐标点是否在路径内, 提供了 isPointInStroke() 判断一个坐标点是否在描边的边上。利用这两个API我们可以实现几乎所有类型的图形对象拾取。

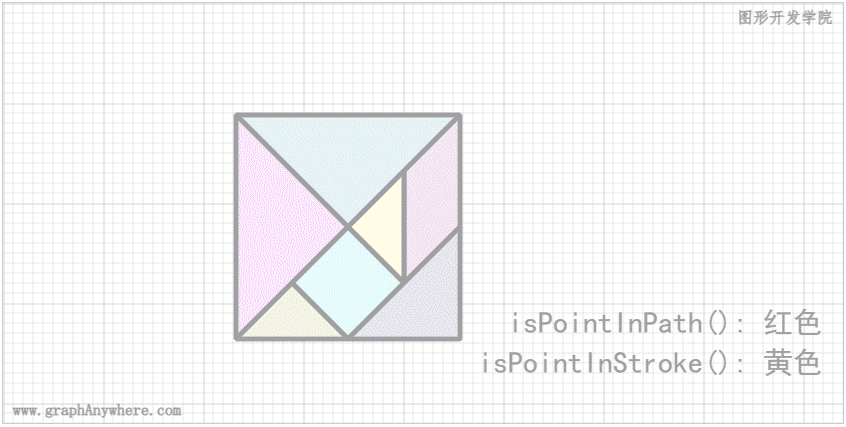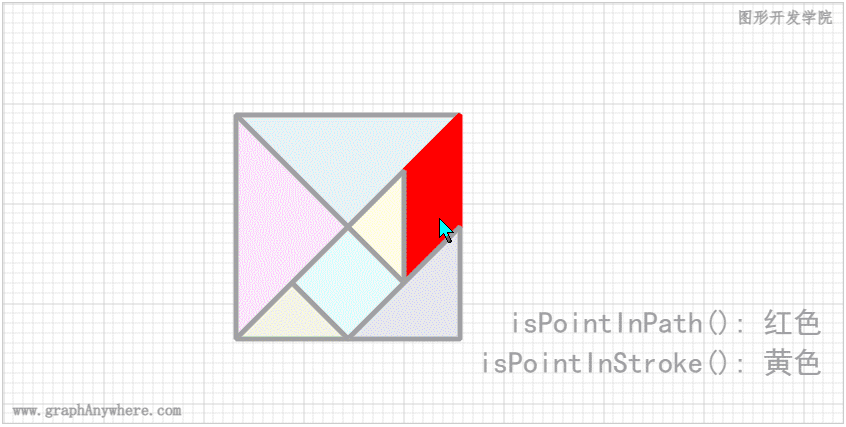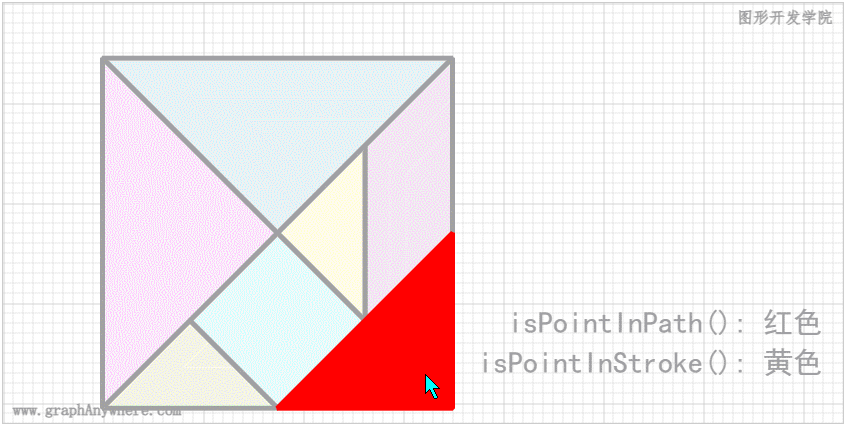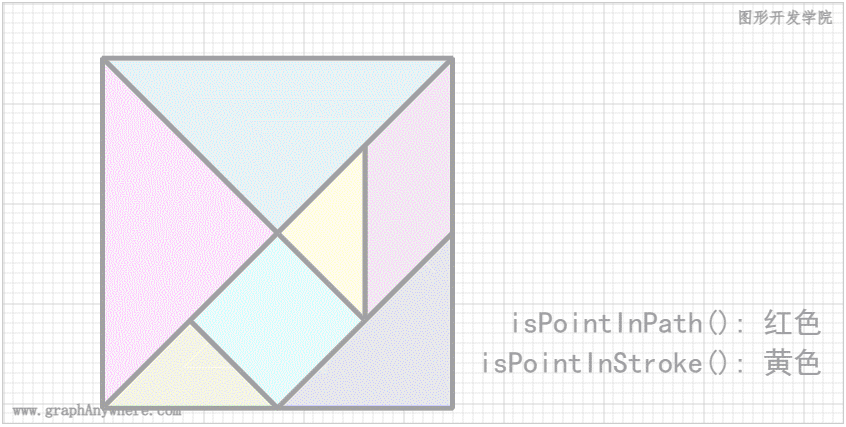
$\quad$ 下面这个示例是在上一篇文章图形交互：图形交互操作:平移和缩放中的示例基础上做出了一些改变，在 redraw() 方法中增加了 point参数，该参数为鼠标当前的位置。当鼠标移动到某个方块内的时候，即 isPointInPath()返回true，该方块将会显示为红颜色；当鼠标移动到某个方块边缘的时候，即 isPointInStroke()返回true，该方块将会显示为黄颜色。运行效果如下图所示：

在这里插入图片描述

$\quad$ 这个示例中采用了 Canvas 渲染上下文对象提供的 isPointInPath() 和 isPointInStroke() 方法判断点是否在路径中或边框之上。其源代码如下：

// 绘图
function redraw(point) {
    // 清除已有内容
    ctx.clearRect(0, 0, canvas.width, canvas.height);

    // 绘制七巧板
    tangram.forEach(shape => {
        // 坐标转换
        let pixel = [];
        shape.coords.forEach(coord => {
            pixel.push(convert(coord, graphExtent, canvasExtent));
        })

        // 定义路径
        ctx.beginPath();
        for (let i = 0, ii = pixel.length; i < ii; i += 1) {
            if (i === 0) {
                ctx.moveTo(pixel[i][0], pixel[i][1]);
            } else {
                ctx.lineTo(pixel[i][0], pixel[i][1]);
            }
        }
        ctx.closePath();

        // 定义渲染颜色值
        let fillColor = shape.style.fillColor;
        let strokeColor = shape.style.color; 

        // 如果Point参数为空，则无需进行碰撞检测
        if (point != null && point.length == 2) {
            // 判断点是否在路径内， 如果在路径内，则将颜色改为红色
            if (ctx.isPointInPath(point[0], point[1])) {
                fillColor = "red";
                strokeColor = "red"
            } 
            // 判断点是否在路径的描边线上， 如果在路径内，则将颜色改为金色
            else {
                if (ctx.isPointInStroke(point[0], point[1])) {
                    fillColor = "gold";
                    strokeColor = "gold";
                }
            }
        }

        // 绘制
        ctx.save();
        ctx.strokeStyle = strokeColor;
        ctx.fillStyle = fillColor;
        ctx.fill();
        ctx.stroke();
        ctx.restore();
    })
}

使用该方法需要注意:

我们在第四章图形基本形状讲述的图形对象类型包括：点、线、多边形、图像、文本、圆等，其中文本类型和图像类型无法通过该方法判断是否与点碰撞。
如果点存在大小时，该方法仅能判断其中心是否在路径内，而无法判断点的边缘是否在路境内。
在使用 isPointInPath(x, y) 和 isPointInStroke(x, y) 方法判断点是否在路径中或边框之上的时候，这个点(x,y)坐标是指画布中的像素坐标。如果画布在绘制路径之前进行了变形操作，参数依旧需传入画布变形前的像素坐标值。

2 几何法

$\quad$ 几何法是指根据点的位置，采用几何算法判断该位置是否存在图形对象。我们在第四章图形基本形状讲述的图形对象类型包括：点、线、矩形、多边形、图像、文本、圆等等。使用几何法进行判断时，需要分别对这些类型进行判断。

2.1 点与点

判断规则：

$\quad$ 判断点与点是否相交，最简单的判断方法是两个点的坐标是否相等，如果相等则判断这两个点相交，而实际绘图的点是有大小的，而且由于浮点误差方面的原因，不能简单判断点与点是否相等，而因改为计算点与点之间的距离，如果这个距离小于容差值，则判断这两个点相交。

实现代码：

/**
 * 判断点与点是否碰撞
 * @param {Point} p1 {x, y}
 * @param {Point} p2 {x, y}
 * @param {float} buffer 
 * @returns boolean
 */
function pointPoint(point1, point2, buffer) {
    if (buffer === undefined) {
        buffer = 0.1;
    }
    if (CoordUtil.dist([point1.x, point1.y], [point2.x, point2.y]) <= buffer) {
        return true;
    }
    return false;
}

运行效果：

在这里插入图片描述

2.2 点与圆

判断规则：

$\quad$ 判断点与圆是否相交的规则和判断点与点是否相交的规则类似，通过计算点与圆心之间的距离，如果距离小于等于圆的半径，则判断点在圆内，否则判断点不在圆内。

实现代码：

/**
 * 判断点与圆是否碰撞
 * @param {Point} p {x, y}
 * @param {Circle} c {cx, cy, radius}
 * @returns boolean
 */
function pointCircle(point, circle) {
    if (CoordUtil.dist([point.x, point.y], [circle.cx, circle.cy]) <= circle.radius) {
        return true;
    }
    return false;
};

运行效果：

在这里插入图片描述

2.3 点与线

判断规则：

$\quad$ 判断点与线是否相交的规则：分别计算点与线的两个端点之间的距离，如果距离之和等于线的长度，则可判定点与线相交。

实现代码：

/**
 * 判断点与线段是否碰撞
 * @param {*} point {x, y}
 * @param {*} line {x1, y1, x2, y2}
 * @param {*} buffer 容差
 * @returns boolean
 */
function pointLine(point, line, buffer) {
    if (buffer === undefined) {
        buffer = 0.1;
    }

    // 计算点与线段的两个端点之间的距离
    let d1 = Coordinate.dist([point.x, point.y], [line.x1, line.y1]);
    let d2 = Coordinate.dist([point.x, point.y], [line.x2, line.y2]);

    // 计算线段长度
    let lineLen = Coordinate.dist([line.x1, line.y1], [line.x2, line.y2]);

    // 如果点与线段的两个端点之间的距离之和等于线的长度，则可判定点与线相交
    if (d1 + d2 >= lineLen - buffer && d1 + d2 <= lineLen + buffer) {
        return true;
    }
    return false;
}

运行效果：

在这里插入图片描述

折线通常包含了多个线段，点与折线是否相交的判断规则是以点与线段是否相交为基础，逐一判断点与每段线的关系。点只要与其中任何一段线相交，即可判段点与折线相交。

2.4 点与矩形

判断规则：

$\quad$ 判断点与矩形是否相交的规则：当点的X坐标大于等于矩形的起点X坐标，小于等于矩形的起点X坐标加上矩形宽度，且点的Y坐标大于等于矩形的起点Y坐标，小于等于矩形的起点Y坐标加上矩形高度时，判断点在矩形内，否则判断点不在矩形内。

实现代码：

/**
 * 判断点与矩形是否碰撞
 * @param {*} point {x, y}
 * @param {*} rect {x, y, width, height}
 * @returns boolean
 */
function pointRect(point, rect) {
    if (point.x >= rect.x && point.x <= rect.x + rect.width &&    // X坐标大于等于矩形的起点X坐标，小于等于矩形的起点X坐标加上矩形宽度
        point.y >= rect.y && point.y <= rect.y + rect.height) {   // Y坐标大于等于矩形的起点Y坐标，小于等于矩形的起点Y坐标加上矩形高度
        return true;
    }
    return false;
}

运行效果：

在这里插入图片描述

2.5 点与文本

判断规则：

$\quad$ 文本绘制的结果是一个矩形区域，因此其判断点与文本是否相交的方法与矩形一样。需要注意的是在绘制文本的时候 水平对齐方式 和 垂直对齐方式 对文本的绘制位置有很大影响。下面的代码可计算绘制文本时的矩形位置和大小：

/**
 * 返回对象边界
 * @param {Boolean} useCoord 为true时返回坐标Bound，为false时返回屏幕像素Bound
 * @returns {Extent} extent
 */
getBBox(useCoord = true) {
    let coord = useCoord === false ? this.getPixel() : this.getCoord();

    // 矢量字体才考虑宽度和高度对BBOX的影响
    let width = this._renderWidth;   // 渲染文本时记录的文本宽度，可通过ctx.measureText(this.text).width获取
    let height = this._renderHeight;  // 通常为字体大小

    // 根据字体水平对齐方式确定文本的bbox
    let left, top;
    if (this.style.textAlign == "center" || this.style.textAlign == "middle") {
        left = coord[0][0] - width / 2;
    } else if (this.style.textAlign == "right") {
        left = coord[0][0] - width;
    } else {
        left = coord[0][0]
    }
    // 属性值有 top(文本块的顶部), hanging(悬挂基线), middle(文本块的中间), alphabetic(标准的字母基线), ideographic(表意字基线), bottom(文本块的底部)
    if (this.style.textBaseline == "middle") {
        top = coord[0][1] - height / 2;
    } else if (this.style.textBaseline == "bottom" || this.style.textBaseline == "ideographic") {
        top = coord[0][1] - height;
    } else if (this.style.textBaseline == "alphabetic") {
        top = coord[0][1] - height;;
    } else {    // top,  "hanging"
        top = coord[0][1];
    }
    return [left, top, left + width, top + height];
}

运行效果：

在这里插入图片描述

2.6 点与图像

判断规则：

$\quad$ 图像绘制的结果是也一个矩形区域，因此其判断点与文本是否相交的方法与矩形一样，且其Bounding Box的计算较为简单，这里就不展开叙述了。

2.7 点与多边形

$\quad$ 判断点与多边形是否相交的规则是：判断这个点和多边形每条边的位置关系。在一个多条边围成的区域，点在一条边的右侧，这个点可能在多边形内部，也可能在外部。但是如果判断完点和每一条边的左右关系，如果在右边的边是奇数个，那么点就在内部，如果是偶数，那么点就在外部。通过这个规则，就可以判断点是否包含在多边形内。

来源：https://blog.csdn.net/tom_221x/article/details/51861129

$\quad$ 那么，如何判断一个点和一条边的位置关系？这里需要用到一个向量叉积公式。比如，点(x, y)，与线 (x1, y1) (x2, y2) 的位置关系。我们先求出两个向量 (x - x1, y - y1) 和 (x2 - x1, y2 - y1)。对这两个向量做叉积的结果是 (x - x1) * (y2 - y1) - (y - y1) * (x2 - x1)，如果结果是0，那么点在线上。如果结果大于0，点在线的右边。如果结果小于0，点在线的左边。利用这个公式，我们就能判断点是否在多边形的内部还是外部。

实现代码：

/**
 * 判断点与多边形是否碰撞
 * @param {*} point {x, y}
 * @param {*} polygon [[x,y],[x,y],[x,y]]
 * @returns 
 */
function pointPoly(point, polygon) {
    let collision = false;

    // 遍历多边形的每一条边
    let next = 0;
    for (let current = 0; current < polygon.length; current++) {

        // 当前顶点
        let vc = polygon[current];
        // 下一个顶点
        next = (current === polygon.length - 1 ? 0 : current + 1);
        let vn = polygon[next]; 

        // 判断一个点和一条边(vc,vn)的位置关系, 如果两个检查都为 true，则切换到其相反的值
        if ((vc[1] >= point.y && vn[1] < point.y) || (vc[1] < point.y && vn[1] >= point.y)) {
            // 求出两个向量(x - x1, y - y1) 和 (x2 - x1, y2 - y1), 
            // 并对两个向量做叉积的 (x - x1) * (y2 - y1) - (y - y1) * (x2 - x1)
            if ((point.x - vc[0]) < (point.y - vc[1]) * (vn[0] - vc[0]) / (vn[1] - vc[1])) {
                // 如果结果为零: 表示点在线上
                // 如果结果为正: 表示点在线的右边
                // 如果结果为负: 表示点在线的左边
                collision = !collision;
            }
        }
    }
    return collision;
}

运行效果：

在这里插入图片描述

点与多边形是否相交的几何判断方法很重要，2.4节中讲述了点与矩形的判断方法，那种方法在矩形旋转后，就无法判断了。而对于旋转的矩形可将计算矩形旋转后各个角的坐标值，然后将其转换为多边形，采用点与多边形是否相交的办法进行判断。

3. 取色法

$\quad$ 取色法的核心思想是在绘制图像的同时，在另一个Canvas中绘制一份与当前图形中各个对象坐标位置和大小均相同，且使用独一无二颜色绘制的图形（缓存图形），同时还需保存一份图形颜色与图形对象的对照表。利用 Canvas 渲染上下文对象提供的像素操作API，在进行拾取操作时，从缓存图形中根据点的位置获取相应的颜色信息，并从颜色对照表中取出对应的图形对象。

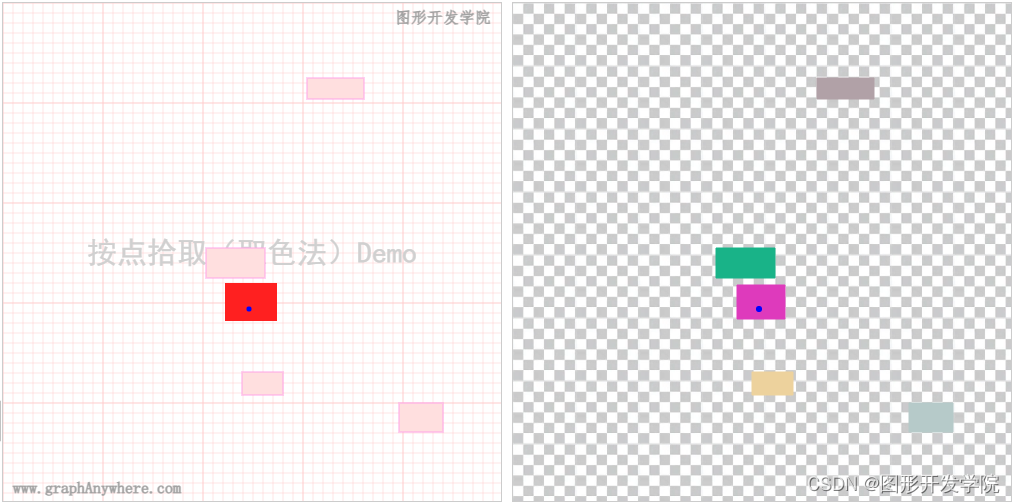
$\quad$ 下图展示了取色法的核心思想，图形的左侧是要绘制的图形，图形的右侧是缓存的图形，这份缓存图形中中的对象位置和大小和原图完全一样，而颜色却是随机产生的独一无二的颜色。使用 Canvas 渲染上下文对象的 ctx.getImageData(x, y, 1, 1) 方法，可取的指定位置那个像素的颜色，最后通过颜色与图形对象对照表即可取得拾取的对象。

在这里插入图片描述

$\quad$ ctx.getImageData() 返回的数据中包含了 data 属性，该属性属于Uint8ClampedArray类型，存储了像素数据，每个像素包含了4个byte的值，分别是该像素对应的红，绿，蓝和透明值(r,g,b,a)。下图显示了imageData中data的数组结构，每个像素均占了data数组中的4个元素，第一个像素存储在data数组的0至3个元素，第二个像素存储在data数组的4至7个元素。

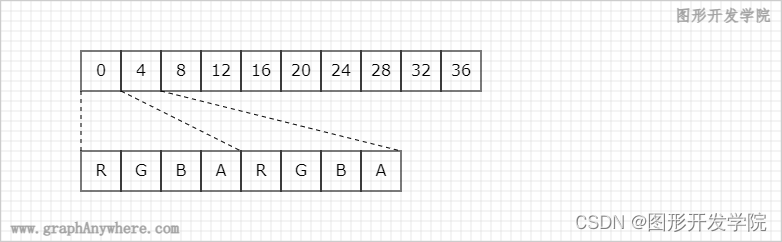
在这里插入图片描述

$\quad$ 我们这里仅拾取了1个像素值，因此该数组仅包含4个元素。拾取指定位置颜色的代码如下所示：

/**
 * 获取图形中指定位置的颜色值
 * @param {Array} point 
 * @returns color
 */
function getColor(point) {
    if (this._hitContext) {
        let imageData = this._hitContext.getImageData(point[0], point[1], 1, 1);
        if (imageData.data[0] === 0 && imageData.data[1] === 0 && imageData.data[2] === 0 && imageData.data[3] === 0) {
            return null;
        } else {
            return new Color(imageData.data[0], imageData.data[1], imageData.data[2], imageData.data[3]).toHex();
        }
    } else {
        return null;
    }
}

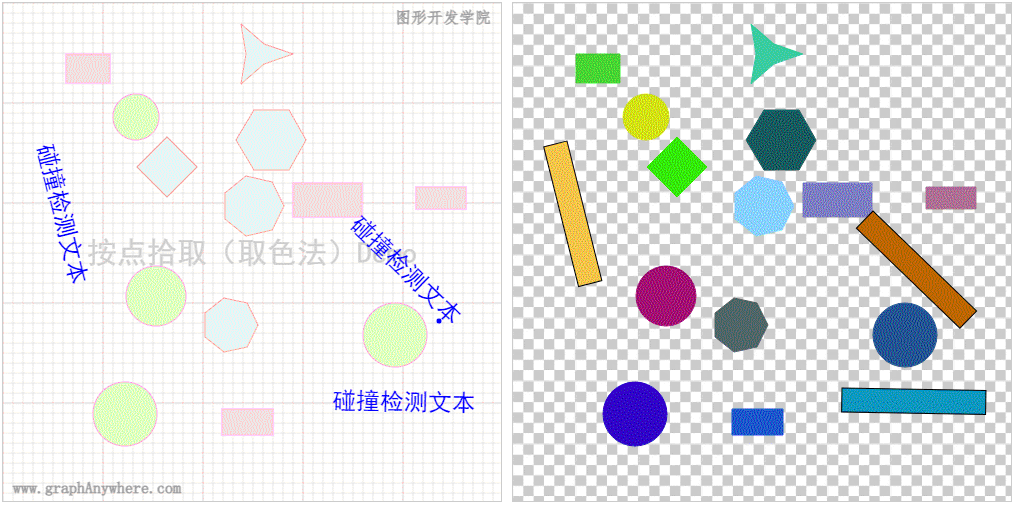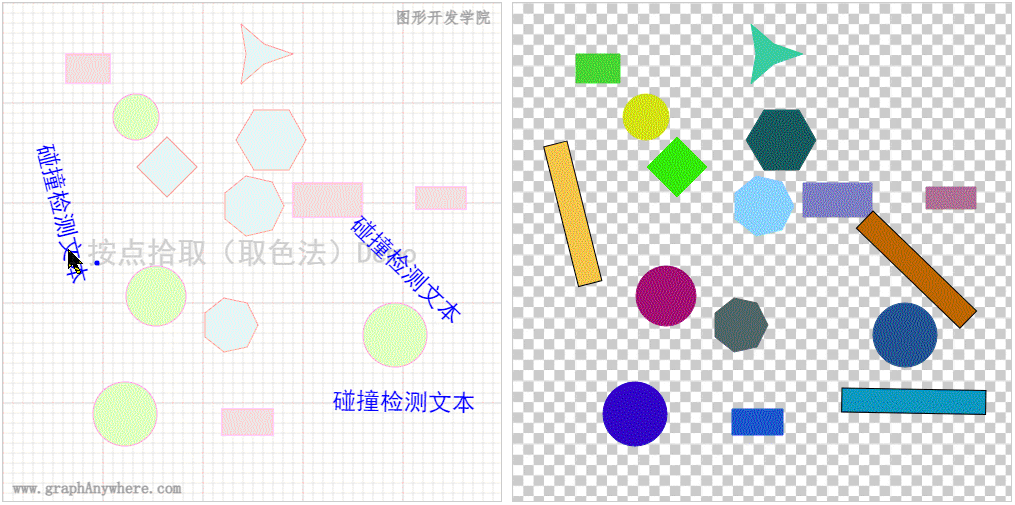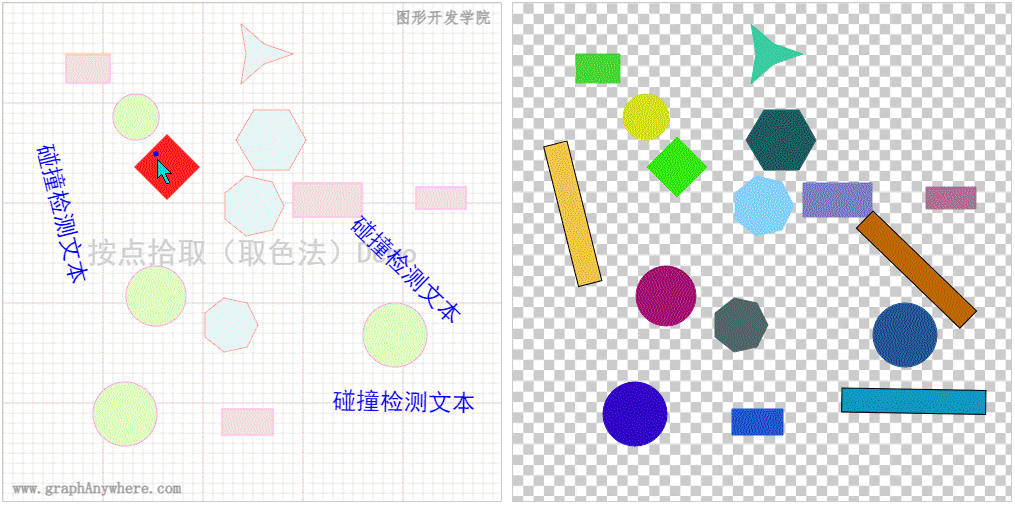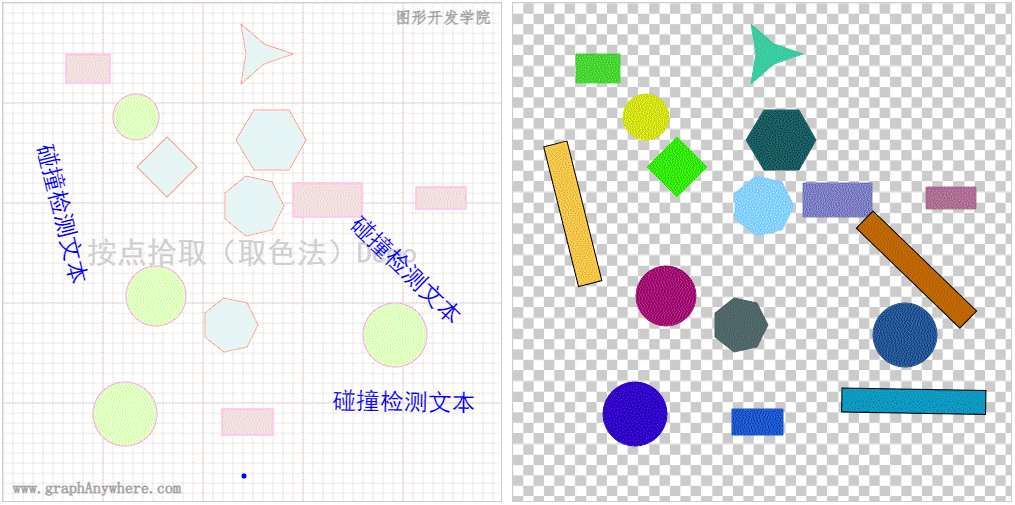
$\quad$ 对于常见的几何图形，使用这个思路直接在缓存的图形中绘制即可。对于文本和图像，则需要将其转换为矩形，通过矩形的方式绘制在缓存的图形中。下图演示了使用 取色法 从一张包含了各类图形对象的图形中拾取对象的效果。

在这里插入图片描述

4. 方案比较

4.1 内置API法

优点：

开发简单；
识别率高；

缺点：

拾取效率低，拾取的时候定义路径导致拾取效率低；
无法拾取非路径绘制的图形，例如文本和图像；
无法实现根据矩形或多边形进行拾取；

4.2 几何法

优点：

扩展性强；
识别率高；

缺点：

开发复杂，需针对各种类型的图形分别实现其算法；
拾取效率一般；

4.3 取色法

优点：

开发简单；
拾取效率高；

缺点：

渲染开销加倍，每次图形渲染时间为内置API法或几何法的两倍；
当图形重叠时，仅能识别到最上层的图形对象；
无法实现根据矩形或多边形进行拾取；

5. anyGraph 的实现

anyGraph 实现了几何法和取色法两种图形对象的拾取方案。

5.1 取色法

Graph 对象在初始化时可通过 hitGetColor 选项，指定是否启用‘取色法拾取方案’。该参数的缺省值为 false。

下面这段代码启用了‘取色法拾取方案’。

// graph对象
let graph = new Graph({
    "target": "graphWrapper",
    "hitGetColor": true
});

下面这段代码演示了取色法的碰撞检测：

// 取色法进行碰撞检测
function _collideCheck(coord) {
    // 显示颜色值
    let hitColor = graph.getRenderer().getColor(coord);
    if (hitColor) {
        if (graph.viewGeomList.has(hitColor)) {
            let clone = graph.viewGeomList.get(hitColor).clone();

            // 在浮动层突出显示拾取的对象
            clone.setStyle({ "fillColor": "gold", "color": "gold" });
            overLayer.getSource().add(clone);
            return true;
        }
    }
    return false;
}

5.2 几何法

$\quad$ anyGraph 图形基本形状类 Geometry对象提供了 contain(point)方法，各子类均已实现了该方法，通过该方法可判断图形对象与点的位置关系。

$\quad$ 下面这段代码演示了几何法的碰撞检测：

// 逐一与数据层中的对象进行碰撞检测
function _collideCheck(coord) {
    let datas = layer.getSource().getData();
    for (let i = 0, len = datas.length; i < len; i++) {
        if (datas[i].contain([coord[0], coord[1]])) {
            let clone = datas[i].clone();
            clone.setStyle({ "fillColor": "#FF2020", "color": "#FF2020", "lineWidth":4 });
            overLayer.getSource().add(clone);
            return true;
        }
    }
    return false;
}