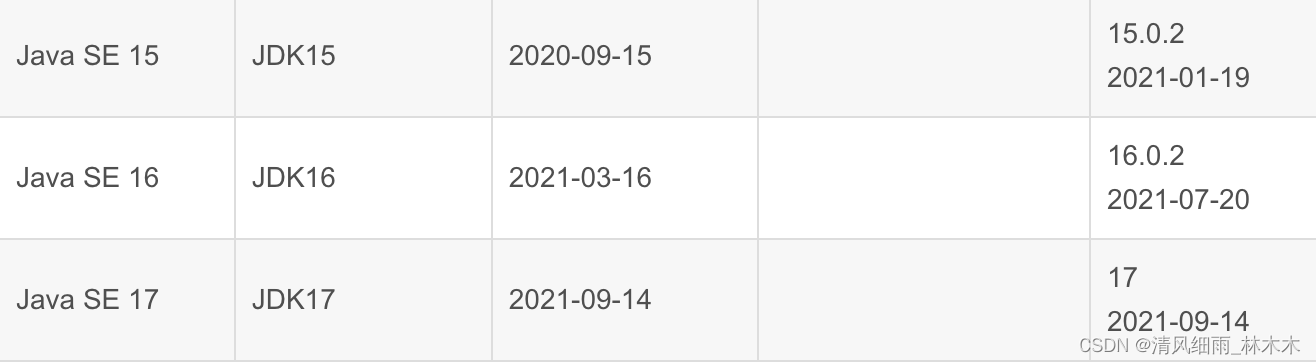
解法一：双指针

首先，每次操作可以移除数组 nums 最左边或最右边的元素，那么相当于求出$l和r$使得$[0,l]+[r,n-1]$之间所有元素之和等于$x$,并且元素个数最少。我们可以通过双重循环枚举$l和r变量$的取值来计算出最小的答案。时间复杂度为$O(n^2)$。


但其实很多区间是不合法的，比如若$[0,l]$的和已经大于x,那么对于当前的$l$就不用再去枚举$r$。通过这种思路，我们使用双指针进行优化。


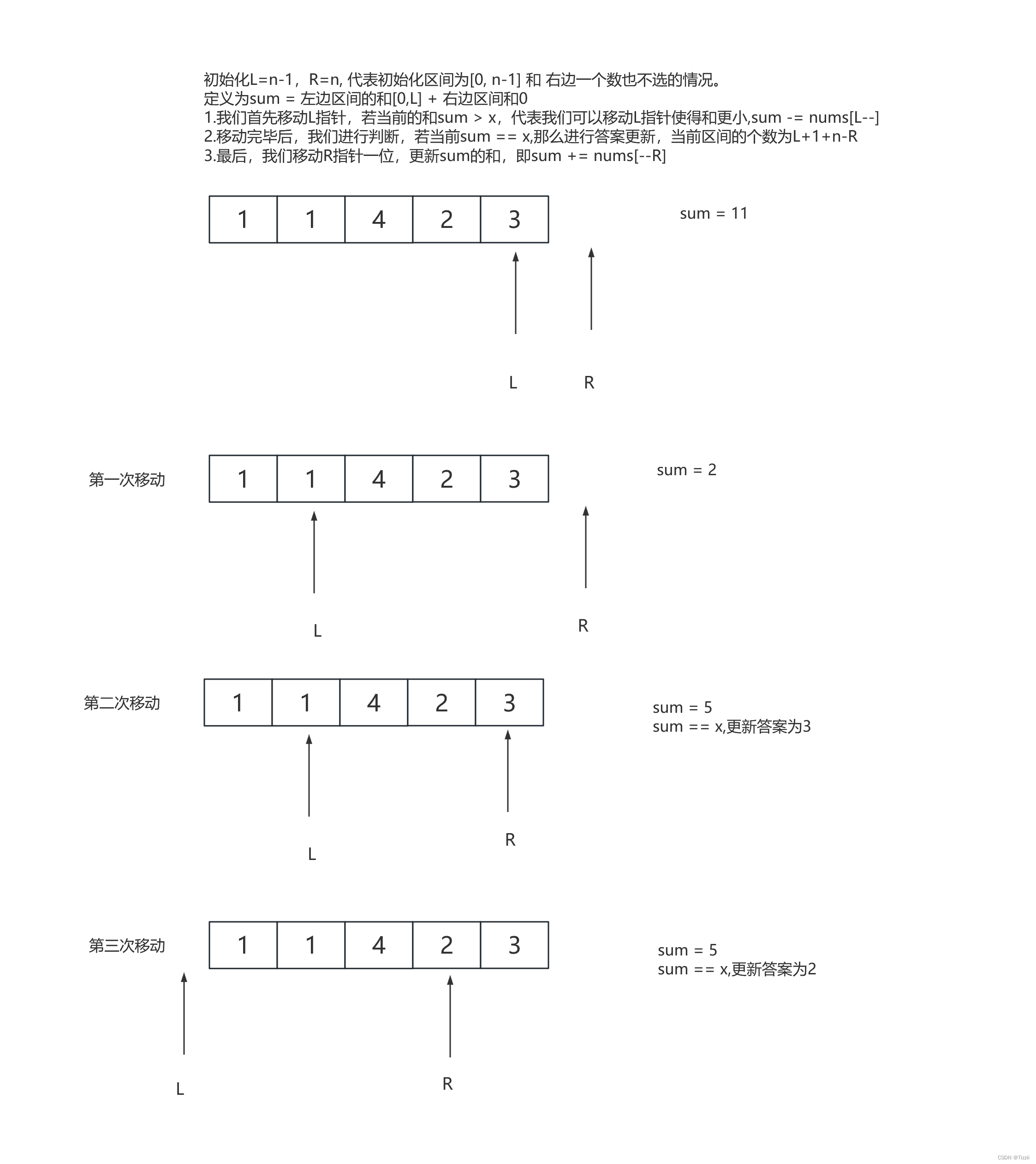$R和L$指针移动的次数都为n,因此整个时间复杂度为$O(n)$。对于第一次移动来说，先让$L$指针移动是为了直接计算右边区间长度为0的情况。对于$-1$的情况，若我们的ans最后大于n，那么必然不合法。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$
• 相似题目：2516. 每种字符至少取 K 个 1423. 可获得的最大点数

class Solution {
    public int minOperations(int[] nums, int x) {
        int sum = Arrays.stream(nums).sum(), n = nums.length, l = n - 1, ans = n + 5;
        for (int r = n - 1; r >= 0; r--) {
            while (sum > x && l >= 0) sum -= nums[l--];
            if (sum == x) ans = Math.min(ans, n - r + l); 
            sum += nums[r]; 
        }
        return ans > n ? -1 : ans;
    }
}

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int sum = accumulate(nums.begin(), nums.end(), 0), n = nums.size(), l = n - 1, ans = n + 5;
        for (int r = n - 1; r >= 0; r--) {
            while (sum > x && l >= 0) sum -= nums[l--];
            if (sum == x) ans = min(ans, n - r + l);
            sum += nums[r]; 
        }
        return ans > n ? -1 : ans;
    }
};

class Solution:
    def minOperations(self, nums: List[int], x: int) -> int:
        n = len(nums)
        s, l, ans = sum(nums), n - 1, n + 5
        for r in range(n - 1, -1, -1):
            while s > x and l >= 0:
                s -= nums[l]
                l -= 1
            if s == x:
                ans = min(ans, n - r + l)
            s += nums[r]
        return -1 if ans > n else ans
         

如果有问题,欢迎评论区交流, 如果有帮助到你，请给题解点个赞和收藏哈~~~