1 统计指标的方法

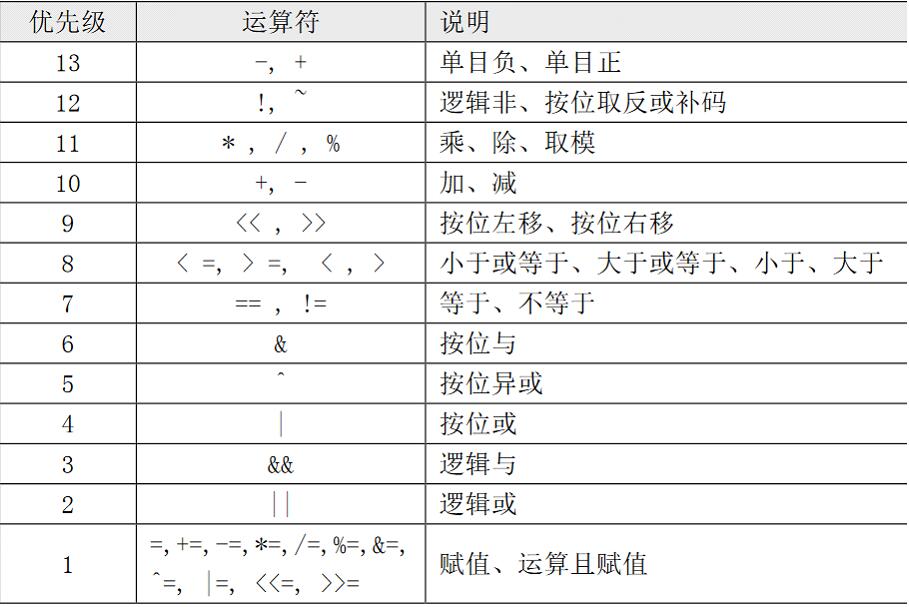
1.1群体稳定性指标（Population Stability Index，PSI）

群体稳定性指标（Population Stability Index，PSI）， 衡量未来的样本（如测试集）及训练样本评分的分布比例是否保持一致，以评估数据/模型的稳定性（按照经验值，PSI<0.1分布差异是比较小的。）。

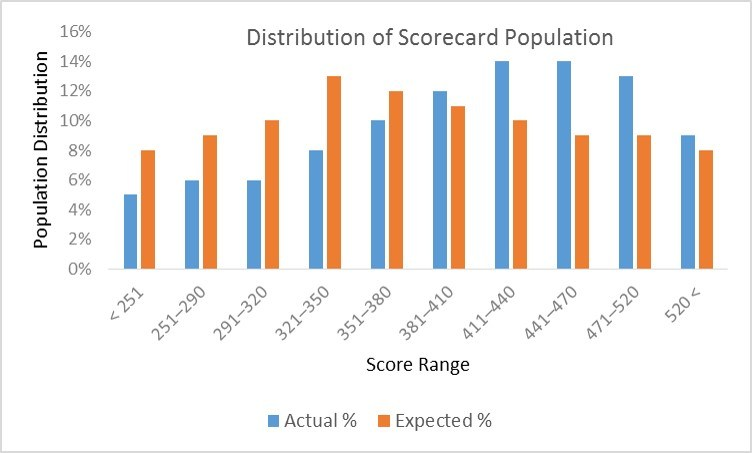
同理，PSI也可以细化衡量特征值的分布差异，评估数据特征层面的稳定性。PSI指标计算公式为 SUM(各分数段的 (实际占比 - 预期占比）* ln(实际占比 / 预期占比) )，

计算公式：

分析psi指标原理，经过公式变形，我们可以发现psi的含义等同于第一项实际分布（A）与预期分布（E）的KL散度 + 第二项预期分布（E）与实际分布（A）之间的KL散度之和，KL散度可以单向（非对称性指标）地描述信息熵差异，上式更为综合地描述分布的差异情况。

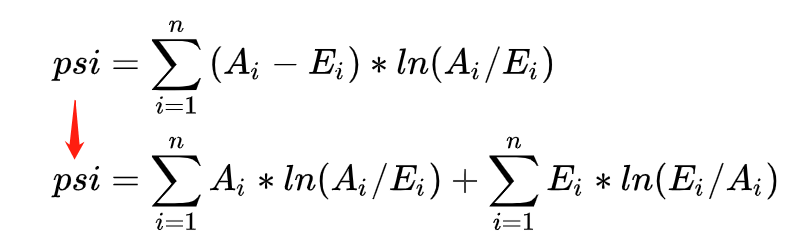
PSI数值越小（经验是常以<0.1作为标准），两个分布之间的差异就越小，代表越稳定。

具体的计算步骤及示例代码如下：

step1：将预期数值分布（开发数据集）进行分箱离散化，统计各个分箱里的样本占比。

step2: 按相同分箱区间，对实际分布（测试集）统计各分箱内的样本占比。

step3:计算各分箱内的A - E和Ln(A / E)，计算index = (实际占比 - 预期占比）* ln(实际占比 / 预期占比) 。

step4: 将各分箱的index进行求和，即得到最终的PSI

import math
import numpy as np
import pandas as pd

def calculate_psi(base_list, test_list, bins=20, min_sample=10):
    try:
        base_df = pd.DataFrame(base_list, columns=['score'])
        test_df = pd.DataFrame(test_list, columns=['score']) 
        
        # 1.去除缺失值后，统计两个分布的样本量
        base_notnull_cnt = len(list(base_df['score'].dropna()))
        test_notnull_cnt = len(list(test_df['score'].dropna()))

        # 空分箱
        base_null_cnt = len(base_df) - base_notnull_cnt
        test_null_cnt = len(test_df) - test_notnull_cnt
        
        # 2.最小分箱数
        q_list = []
        if type(bins) == int:
            bin_num = min(bins, int(base_notnull_cnt / min_sample))
            q_list = [x / bin_num for x in range(1, bin_num)]
            break_list = []
            for q in q_list:
                bk = base_df['score'].quantile(q)
                break_list.append(bk)
            break_list = sorted(list(set(break_list))) # 去重复后排序
            score_bin_list = [-np.inf] + break_list + [np.inf]
        else:
            score_bin_list = bins
        
        # 4.统计各分箱内的样本量
        base_cnt_list = [base_null_cnt]
        test_cnt_list = [test_null_cnt]
        bucket_list = ["MISSING"]
        for i in range(len(score_bin_list)-1):
            left  = round(score_bin_list[i+0], 4)
            right = round(score_bin_list[i+1], 4)
            bucket_list.append("(" + str(left) + ',' + str(right) + ']')
            
            base_cnt = base_df[(base_df.score > left) & (base_df.score <= right)].shape[0]
            base_cnt_list.append(base_cnt)
            
            test_cnt = test_df[(test_df.score > left) & (test_df.score <= right)].shape[0]
            test_cnt_list.append(test_cnt)
        
        # 5.汇总统计结果    
        stat_df = pd.DataFrame({"bucket": bucket_list, "base_cnt": base_cnt_list, "test_cnt": test_cnt_list})
        stat_df['base_dist'] = stat_df['base_cnt'] / len(base_df)
        stat_df['test_dist'] = stat_df['test_cnt'] / len(test_df)
        
        def sub_psi(row):
            # 6.计算PSI
            base_list = row['base_dist']
            test_dist = row['test_dist']
            # 处理某分箱内样本量为0的情况
            if base_list == 0 and test_dist == 0:
                return 0
            elif base_list == 0 and test_dist > 0:
                base_list = 1 / base_notnull_cnt   
            elif base_list > 0 and test_dist == 0:
                test_dist = 1 / test_notnull_cnt
                
            return (test_dist - base_list) * np.log(test_dist / base_list)
        
        stat_df['psi'] = stat_df.apply(lambda row: sub_psi(row), axis=1)
        stat_df = stat_df[['bucket', 'base_cnt', 'base_dist', 'test_cnt', 'test_dist', 'psi']]
        psi = stat_df['psi'].sum()
        
    except:
        print('error!!!')
        psi = np.nan 
        stat_df = None
    return psi, stat_df

## 也可直接调用toad包计算psi
# prob_dev模型在训练样本的评分，prob_test测试样本的评分
psi = toad.metrics.PSI(prob_dev,prob_test)

PSI值优点：

计算便捷

注意：PSI的计算受分组数量及方式、群体样本量和现实业务政策等多重因素影响，尤其是对业务变动剧烈的小样本来说，PSI的值往往超出一般的经验水平，因此需要结合实际的业务和数据情况进行具体分析。

其他的方法如 KS检验，KDE （核密度估计）分布图等方法可见参考链接[2]

1.2 KDE (核密度估计)分布图

核密度估计图(Kernel Density Estimation, KDE)，KDE是非参数检验，用于估计分布未知的密度函数，相比于直方图，它受bin影响更小，绘图呈现更平滑，易于对比数据分布

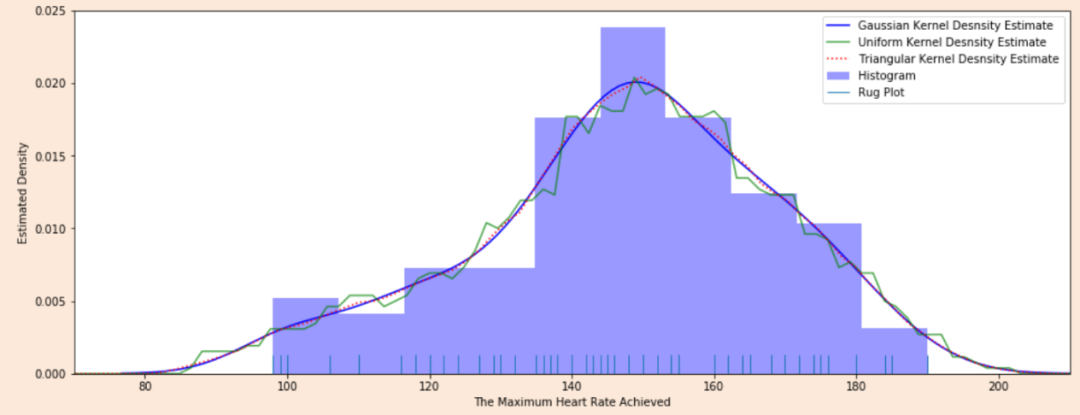
心脏疾病患者最大心率的概率密度函数分布图，数据源自UCI ML开放数据集

KDE计算公式:

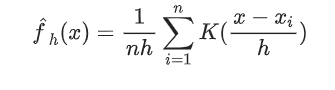
是来自未知分布的样本， n 是样本总数，K 是核函数，h是带宽(Bandwidth)。

核函数定义一个用于生成PDF(概率分布函数Probability Distribution Function)的曲线，不同于将值放入离散bins内，核函数对每个样本值都创建一个独立的概率密度曲线，然后加总这些平滑曲线，最终得到一个平滑连续的概率分布曲线，如下图所示:

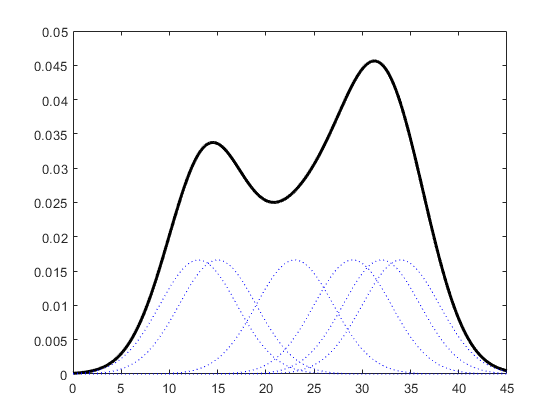
生成KDE的过程呈现

python代码：可以用seaborn.kdeplot()进行绘图可视化

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# 创建样例特征
train_mean, train_cov = [0, 2], [(1, .5), (.5, 1)]
test_mean, test_cov = [0, .5], [(1, 1), (.6, 1)]
train_feat, _ = np.random.multivariate_normal(train_mean, train_cov, size=50).T
test_feat, _ = np.random.multivariate_normal(test_mean, test_cov, size=50).T

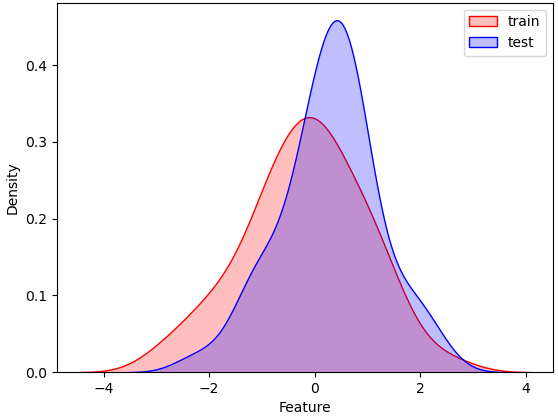
# 绘KDE对比分布
sns.kdeplot(train_feat, shade = True, color='r', label = 'train')
sns.kdeplot(test_feat, shade = True, color='b', label = 'test')
plt.xlabel('Feature')
plt.legend()
plt.show()

1.3 KS检验

KDE是PDF来对比，而KS检验是基于CDF(累计分布函数Cumulative Distribution Function)来检验两个数据分布是否一致，它也是非参数检验方法(即不知道数据分布情况)。两条不同数据集下的CDF曲线，它们最大垂直差值可用作描述分布差异(见下图中的D)。

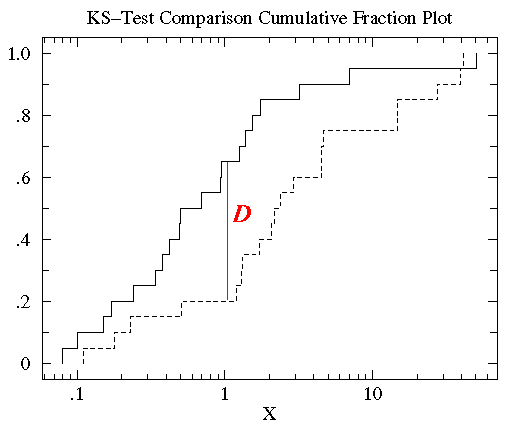
python代码：调用scipy.stats.ks_2samp()得到KS的统计值(最大垂直差)和假设检验下的p值：

from scipy import stats
stats.ks_2samp(train_feat, test_feat)
输出：KstestResult(statistic=0.2, pvalue=0.2719135601522248)

若KS统计值小且p值大，则我们可以接受KS检验的原假设H0，即两个数据分布一致。上面样例数据的统计值较低，p值大于10%但不是很高，因此反映分布略微不一致。注意: p值<0.01，强烈建议拒绝原假设H0，p值越大，越倾向于原假设H0成立。

2异常点检测的方法

可以通过训练数据集训练一个模型（如 oneclass-SVM），利用模型判定哪些数据样本的不同于训练集分布（异常概率）。相关算法参考：

【异常检测】14种异常检测算法_allein_STR的博客-CSDN博客_异常行为监测算法有哪些

3分类的方法--对抗验证

思路是：

混合训练数据与测试数据（测试数据可得情况），将训练数据与测试数据分别标注为’1‘和’0‘标签，进行分类，若一个模型，可以以一个较好的精度将训练实例与测试实例区分开，说明训练数据与测试数据的特征值分布有较大差异，存在协变量偏移。

相应的对这个分类模型贡献度比较高的特征，也就是分布偏差比较大的特征。分类较准确的样本（简单样本）也就是分布偏差比较大的样本。。

具体步骤如下:

• 训练集和测试集合并，同时新增标签‘Is_Test’去标记训练集样本为0，测试集样本为1。

• 构建分类器(例如LGB, XGB等)去训练混合后的数据集(可采用交叉验证的方式)，拟合目标标签‘Is_Test’。

• 输出交叉验证中最优的AUC分数。AUC越大(越接近1)，越说明训练集和测试集分布不一致。

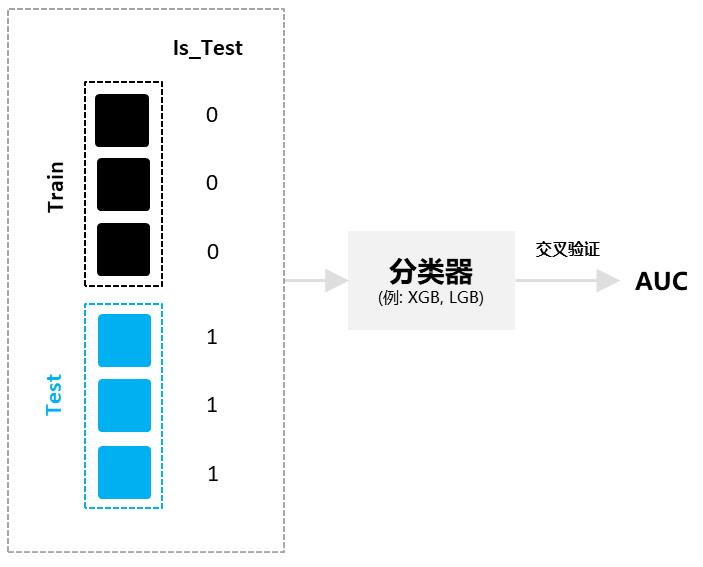
对抗验证示意图

python代码：

Adversarial_Validation - Qiuyuan918, 代码: https://github.com/Qiuyan918/Adversarial_Validation_Case_Study/blob/master/Adversarial_Validation.ipynb