背景
中值滤波,最大值滤波,最小值滤波属于排序滤波,常用于图像去噪处理。
最大/小值滤波的处理比较好理解,就是逐个比较窗口内的每个数字,每次比较会根据所属任务保留最大值,或最小值。假设滑动窗口是3*3,则窗口内9个数进行8次比较,就能得到最大/小值滤波的一个结果。
中值滤波,顾名思义,指的是对窗口内的数取中值,作为滤波处理的结果。如果不考虑优化的实现思路,就是把窗口内所有元素进行排序,然后取中间的值,排序算法的时间复杂度最小的是nlog(n),也就是需要进行n*log(n)次比较,当n=9时候,对全部数据进行排序需要进行至少27次比较。
实际上,中值滤波只需要知道窗口内的中值是几,而不需要对全部数据进行排序,基于这样的考虑,就能减少比较的次数。
opencv源码解读
中值滤波在opencv的源码路径是:modules/imgproc/src/smooth.cpp中。源码附在最后了。
opencv的中值滤波实现支持3*3, 5*5的滤波尺寸。通过定义排序网络实现中值滤波。
排序网络的设计思想是定义两种比较器:一种是OP,OP算子实现的是传入两个数a,b, 通过OP比较器后将a,b中大的数赋值给b, 小的数赋值给a;另一中比较器是VOP,VOP则是指传入的va,vb是具有相同元素的向量,同OP一样,向量中元素一一对应相比较,大数存放在vb中,小数存放在va中。这种VOP是指计算机支持硬件加速的话,会打开useSIMD的开关,使用CPU指令集加速任务进度。
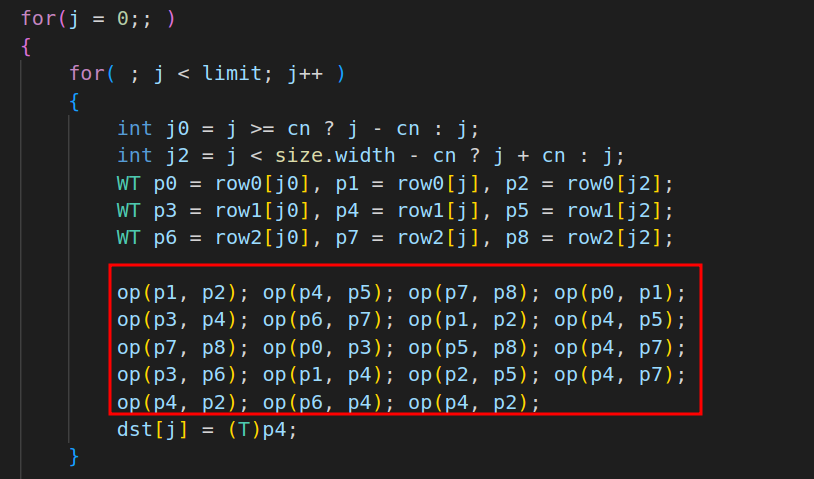
如下图,源码的核心是如下定义比较器,当窗口为3*3时候,只进行了19次比较,就得到了中值。为什么能这样呢?这里就用到了算法的思想。
简化后的算法问题是,给9个数,如何通过最少的比较次数,得到这9个数的中值。
关于比较次数的三分法理解
https://www.cnblogs.com/olivermahout/p/9346353.html介绍了采用三分法的原理,对于每一行进行比较,然后再通过一轮比较得到最终结果。对于9个数字取中位数一共只用到了21个两两比较器。
如下图
1,第一轮比较,9次。 A 1是指对第1行的3个数排序比较,A2是对第2行的3个数进行排序比较,A3是对第3行的3个数进行排序比较;
2, 第二轮比较,9次。B1汇聚了A1,A2,A3的最大值,B2汇聚了A1,A2,A3的中间值,B3汇聚了A1,A2,A3的最小值。将B1,B2,B3中的三个数进行比较。
3, 第三轮比较,3次。C汇聚了B1,B2,B3中的分别最小值,中间值,最大值。比较C中3个值的大小,输出中间值,就是这9个数的中值。
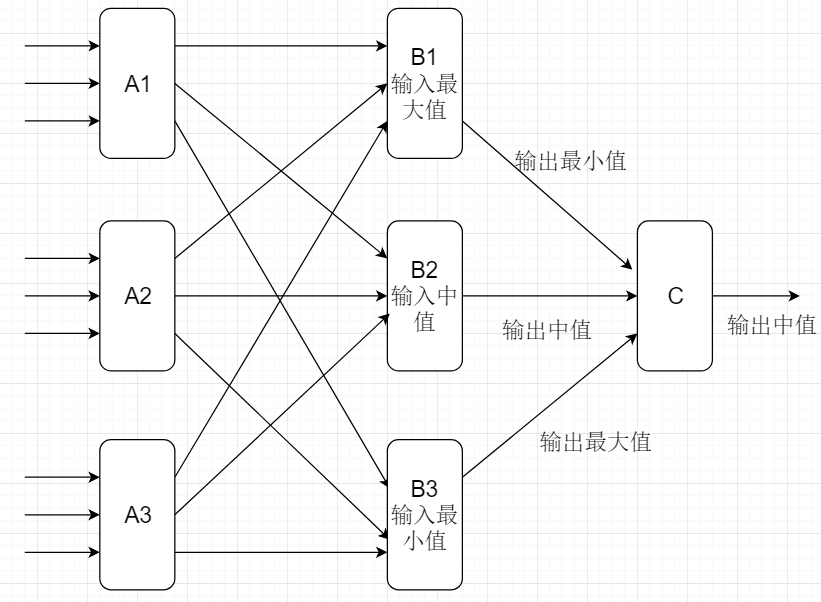
这里,你肯定好奇,为什么B1,B2,B3是这样取A1,A2,A3的比较结果,C这样取B1,B2,B3的比较结果呢?为什么这样设计得到的就是这9个数的中值呢?下面结合opencv的代码设计来解释。
关于比较次数的opencv设计理解
opencv的比较器比上面3分法的比较次数少了2次,9个数进行19次两两比较就能得到中值。但是实际的思路是一样。优化的点在于B1,B3中的比较分别是少了1次。
opencv的整体思路是进行了4轮比较(ps:不相关的数的比较可以设计并行执行):
第1轮,把三行数,每行内的3个数进行排序;
第2轮,排除掉9个数中的两个是中值的可能;
第3轮,排除掉剩余7个数中的4个是中值的可能;
第4轮,比较剩余的3个数,排除掉2个,找到中值。

推理如下:
理解前提:
n是奇数,给n个数取中值,当确定某个数是大于(n+1)/2个数或者小于(n+1)/2个数时候,该数不可能是中值。
op(a,b)的定义: 传入a,b的地址,比较a,b两个地址上的数,将较大的数放在b地址上,较小的数放在a地址上。
第1轮比较。这一轮比较,完成了3行数据,每行内的大小排列,即此时p0≤p1≤p2,p3≤p4≤p5,p6≤p7≤p8
op(p1, p2); op(p4, p5); op(p7, p8);
op(p0, p1);op(p3, p4); op(p6, p7);
op(p1, p2); op(p4, p5);op(p7, p8);
第2轮比较。这一轮比较,可以把p0, p8排除是中值的可能。
op(p0, p3); op(p5, p8);
P0: p0至少小于5个数,所以可排除可能。
P8: p0至少大于5个数,所以可排除可能。
第3轮比较。这一轮比较:把P1, P3, P5, P7排除是中值的可能。
op(p4, p7);op(p3, p6);op(p2, p5);
op(p1, p4);
op(p4, p7);
P1: 在前2轮比较中,P2, P5至少大于P1,P4,P7这三个数的两个,这一轮中P1又是P1,P4,P7三个数中的最小数,所以P1小于至少4个数(P2, P5,P4,P7)。排除P1是中值的可能。
P3: 在前2轮比较中,P3小于P4,P5或者P1, P2,这一轮中,P3又是P3, P6,P7中的最小值,所以P3至少小于4个数(P6, P7,(P4,P5)或(P1,P2))。排除P3是中值的可能。
P5: 在前2轮比较中,P5大于P4,P3或者P6, P7,而P2大于P1,至此,P2,P5至少大于3个数了。 这一轮中,P5又是P2, P5中的最大值,所以P5至少大于4个数(P1, P2,(P4,P3)或(P6,P7))。排除P5是中值的可能。
P7: 在前2轮比较中,至少P1,P4,P7这三个数的两个大于P3, P6,这一轮中P7又是P1,P4,P7三个数中的最大数,所以P7大于至少4个数(P1, P3,P4,P6)。排除P7是中值的可能。
第4轮比较。这一轮比较中,3个数找到中间值,需要进行2次比较。得到P4就是中值。
op(p4, p2); op(p6, p4); op(p4, p2);
最后
对于窗口是5*5的中值滤波,比较次数更多,但是实现思想和3*3是一样的。
怎么样,可能这就是算法优化的极致了吧,能少比较1次也是好的。*^ ^*
Opencv源码
放上opencv的源码,不用再辛苦去找了。
template<class Op, class VecOp>
static void
medianBlur_SortNet( const Mat& _src, Mat& _dst, int m )
{
typedef typename Op::value_type T;
typedef typename Op::arg_type WT;
typedef typename VecOp::arg_type VT;
const T* src = (const T*)_src.data;
T* dst = (T*)_dst.data;
int sstep = (int)(_src.step/sizeof(T));
int dstep = (int)(_dst.step/sizeof(T));
Size size = _dst.size();
int i, j, k, cn = _src.channels();
Op op;
VecOp vop;
volatile bool useSIMD = checkHardwareSupport(CV_CPU_SSE2);
if( m == 3 )
{
if( size.width == 1 || size.height == 1 )
{
int len = size.width + size.height - 1;
int sdelta = size.height == 1 ? cn : sstep;
int sdelta0 = size.height == 1 ? 0 : sstep - cn;
int ddelta = size.height == 1 ? cn : dstep;
for( i = 0; i < len; i++, src += sdelta0, dst += ddelta )
for( j = 0; j < cn; j++, src++ )
{
WT p0 = src[i > 0 ? -sdelta : 0];
WT p1 = src[0];
WT p2 = src[i < len - 1 ? sdelta : 0];
op(p0, p1); op(p1, p2); op(p0, p1);
dst[j] = (T)p1;
}
return;
}
size.width *= cn;
for( i = 0; i < size.height; i++, dst += dstep )
{
const T* row0 = src + std::max(i - 1, 0)*sstep;
const T* row1 = src + i*sstep;
const T* row2 = src + std::min(i + 1, size.height-1)*sstep;
int limit = useSIMD ? cn : size.width;
for(j = 0;; )
{
for( ; j < limit; j++ )
{
int j0 = j >= cn ? j - cn : j;
int j2 = j < size.width - cn ? j + cn : j;
WT p0 = row0[j0], p1 = row0[j], p2 = row0[j2];
WT p3 = row1[j0], p4 = row1[j], p5 = row1[j2];
WT p6 = row2[j0], p7 = row2[j], p8 = row2[j2];
op(p1, p2); op(p4, p5); op(p7, p8); op(p0, p1);
op(p3, p4); op(p6, p7); op(p1, p2); op(p4, p5);
op(p7, p8); op(p0, p3); op(p5, p8); op(p4, p7);
op(p3, p6); op(p1, p4); op(p2, p5); op(p4, p7);
op(p4, p2); op(p6, p4); op(p4, p2);
dst[j] = (T)p4;
}
if( limit == size.width )
break;
for( ; j <= size.width - VecOp::SIZE - cn; j += VecOp::SIZE )
{
VT p0 = vop.load(row0+j-cn), p1 = vop.load(row0+j), p2 = vop.load(row0+j+cn);
VT p3 = vop.load(row1+j-cn), p4 = vop.load(row1+j), p5 = vop.load(row1+j+cn);
VT p6 = vop.load(row2+j-cn), p7 = vop.load(row2+j), p8 = vop.load(row2+j+cn);
vop(p1, p2); vop(p4, p5); vop(p7, p8); vop(p0, p1);
vop(p3, p4); vop(p6, p7); vop(p1, p2); vop(p4, p5);
vop(p7, p8); vop(p0, p3); vop(p5, p8); vop(p4, p7);
vop(p3, p6); vop(p1, p4); vop(p2, p5); vop(p4, p7);
vop(p4, p2); vop(p6, p4); vop(p4, p2);
vop.store(dst+j, p4);
}
limit = size.width;
}
}
}
else if( m == 5 )
{
if( size.width == 1 || size.height == 1 )
{
int len = size.width + size.height - 1;
int sdelta = size.height == 1 ? cn : sstep;
int sdelta0 = size.height == 1 ? 0 : sstep - cn;
int ddelta = size.height == 1 ? cn : dstep;
for( i = 0; i < len; i++, src += sdelta0, dst += ddelta )
for( j = 0; j < cn; j++, src++ )
{
int i1 = i > 0 ? -sdelta : 0;
int i0 = i > 1 ? -sdelta*2 : i1;
int i3 = i < len-1 ? sdelta : 0;
int i4 = i < len-2 ? sdelta*2 : i3;
WT p0 = src[i0], p1 = src[i1], p2 = src[0], p3 = src[i3], p4 = src[i4];
op(p0, p1); op(p3, p4); op(p2, p3); op(p3, p4); op(p0, p2);
op(p2, p4); op(p1, p3); op(p1, p2);
dst[j] = (T)p2;
}
return;
}
size.width *= cn;
for( i = 0; i < size.height; i++, dst += dstep )
{
const T* row[5];
row[0] = src + std::max(i - 2, 0)*sstep;
row[1] = src + std::max(i - 1, 0)*sstep;
row[2] = src + i*sstep;
row[3] = src + std::min(i + 1, size.height-1)*sstep;
row[4] = src + std::min(i + 2, size.height-1)*sstep;
int limit = useSIMD ? cn*2 : size.width;
for(j = 0;; )
{
for( ; j < limit; j++ )
{
WT p[25];
int j1 = j >= cn ? j - cn : j;
int j0 = j >= cn*2 ? j - cn*2 : j1;
int j3 = j < size.width - cn ? j + cn : j;
int j4 = j < size.width - cn*2 ? j + cn*2 : j3;
for( k = 0; k < 5; k++ )
{
const T* rowk = row[k];
p[k*5] = rowk[j0]; p[k*5+1] = rowk[j1];
p[k*5+2] = rowk[j]; p[k*5+3] = rowk[j3];
p[k*5+4] = rowk[j4];
}
op(p[1], p[2]); op(p[0], p[1]); op(p[1], p[2]); op(p[4], p[5]); op(p[3], p[4]);
op(p[4], p[5]); op(p[0], p[3]); op(p[2], p[5]); op(p[2], p[3]); op(p[1], p[4]);
op(p[1], p[2]); op(p[3], p[4]); op(p[7], p[8]); op(p[6], p[7]); op(p[7], p[8]);
op(p[10], p[11]); op(p[9], p[10]); op(p[10], p[11]); op(p[6], p[9]); op(p[8], p[11]);
op(p[8], p[9]); op(p[7], p[10]); op(p[7], p[8]); op(p[9], p[10]); op(p[0], p[6]);
op(p[4], p[10]); op(p[4], p[6]); op(p[2], p[8]); op(p[2], p[4]); op(p[6], p[8]);
op(p[1], p[7]); op(p[5], p[11]); op(p[5], p[7]); op(p[3], p[9]); op(p[3], p[5]);
op(p[7], p[9]); op(p[1], p[2]); op(p[3], p[4]); op(p[5], p[6]); op(p[7], p[8]);
op(p[9], p[10]); op(p[13], p[14]); op(p[12], p[13]); op(p[13], p[14]); op(p[16], p[17]);
op(p[15], p[16]); op(p[16], p[17]); op(p[12], p[15]); op(p[14], p[17]); op(p[14], p[15]);
op(p[13], p[16]); op(p[13], p[14]); op(p[15], p[16]); op(p[19], p[20]); op(p[18], p[19]);
op(p[19], p[20]); op(p[21], p[22]); op(p[23], p[24]); op(p[21], p[23]); op(p[22], p[24]);
op(p[22], p[23]); op(p[18], p[21]); op(p[20], p[23]); op(p[20], p[21]); op(p[19], p[22]);
op(p[22], p[24]); op(p[19], p[20]); op(p[21], p[22]); op(p[23], p[24]); op(p[12], p[18]);
op(p[16], p[22]); op(p[16], p[18]); op(p[14], p[20]); op(p[20], p[24]); op(p[14], p[16]);
op(p[18], p[20]); op(p[22], p[24]); op(p[13], p[19]); op(p[17], p[23]); op(p[17], p[19]);
op(p[15], p[21]); op(p[15], p[17]); op(p[19], p[21]); op(p[13], p[14]); op(p[15], p[16]);
op(p[17], p[18]); op(p[19], p[20]); op(p[21], p[22]); op(p[23], p[24]); op(p[0], p[12]);
op(p[8], p[20]); op(p[8], p[12]); op(p[4], p[16]); op(p[16], p[24]); op(p[12], p[16]);
op(p[2], p[14]); op(p[10], p[22]); op(p[10], p[14]); op(p[6], p[18]); op(p[6], p[10]);
op(p[10], p[12]); op(p[1], p[13]); op(p[9], p[21]); op(p[9], p[13]); op(p[5], p[17]);
op(p[13], p[17]); op(p[3], p[15]); op(p[11], p[23]); op(p[11], p[15]); op(p[7], p[19]);
op(p[7], p[11]); op(p[11], p[13]); op(p[11], p[12]);
dst[j] = (T)p[12];
}
if( limit == size.width )
break;
for( ; j <= size.width - VecOp::SIZE - cn*2; j += VecOp::SIZE )
{
VT p[25];
for( k = 0; k < 5; k++ )
{
const T* rowk = row[k];
p[k*5] = vop.load(rowk+j-cn*2); p[k*5+1] = vop.load(rowk+j-cn);
p[k*5+2] = vop.load(rowk+j); p[k*5+3] = vop.load(rowk+j+cn);
p[k*5+4] = vop.load(rowk+j+cn*2);
}
vop(p[1], p[2]); vop(p[0], p[1]); vop(p[1], p[2]); vop(p[4], p[5]); vop(p[3], p[4]);
vop(p[4], p[5]); vop(p[0], p[3]); vop(p[2], p[5]); vop(p[2], p[3]); vop(p[1], p[4]);
vop(p[1], p[2]); vop(p[3], p[4]); vop(p[7], p[8]); vop(p[6], p[7]); vop(p[7], p[8]);
vop(p[10], p[11]); vop(p[9], p[10]); vop(p[10], p[11]); vop(p[6], p[9]); vop(p[8], p[11]);
vop(p[8], p[9]); vop(p[7], p[10]); vop(p[7], p[8]); vop(p[9], p[10]); vop(p[0], p[6]);
vop(p[4], p[10]); vop(p[4], p[6]); vop(p[2], p[8]); vop(p[2], p[4]); vop(p[6], p[8]);
vop(p[1], p[7]); vop(p[5], p[11]); vop(p[5], p[7]); vop(p[3], p[9]); vop(p[3], p[5]);
vop(p[7], p[9]); vop(p[1], p[2]); vop(p[3], p[4]); vop(p[5], p[6]); vop(p[7], p[8]);
vop(p[9], p[10]); vop(p[13], p[14]); vop(p[12], p[13]); vop(p[13], p[14]); vop(p[16], p[17]);
vop(p[15], p[16]); vop(p[16], p[17]); vop(p[12], p[15]); vop(p[14], p[17]); vop(p[14], p[15]);
vop(p[13], p[16]); vop(p[13], p[14]); vop(p[15], p[16]); vop(p[19], p[20]); vop(p[18], p[19]);
vop(p[19], p[20]); vop(p[21], p[22]); vop(p[23], p[24]); vop(p[21], p[23]); vop(p[22], p[24]);
vop(p[22], p[23]); vop(p[18], p[21]); vop(p[20], p[23]); vop(p[20], p[21]); vop(p[19], p[22]);
vop(p[22], p[24]); vop(p[19], p[20]); vop(p[21], p[22]); vop(p[23], p[24]); vop(p[12], p[18]);
vop(p[16], p[22]); vop(p[16], p[18]); vop(p[14], p[20]); vop(p[20], p[24]); vop(p[14], p[16]);
vop(p[18], p[20]); vop(p[22], p[24]); vop(p[13], p[19]); vop(p[17], p[23]); vop(p[17], p[19]);
vop(p[15], p[21]); vop(p[15], p[17]); vop(p[19], p[21]); vop(p[13], p[14]); vop(p[15], p[16]);
vop(p[17], p[18]); vop(p[19], p[20]); vop(p[21], p[22]); vop(p[23], p[24]); vop(p[0], p[12]);
vop(p[8], p[20]); vop(p[8], p[12]); vop(p[4], p[16]); vop(p[16], p[24]); vop(p[12], p[16]);
vop(p[2], p[14]); vop(p[10], p[22]); vop(p[10], p[14]); vop(p[6], p[18]); vop(p[6], p[10]);
vop(p[10], p[12]); vop(p[1], p[13]); vop(p[9], p[21]); vop(p[9], p[13]); vop(p[5], p[17]);
vop(p[13], p[17]); vop(p[3], p[15]); vop(p[11], p[23]); vop(p[11], p[15]); vop(p[7], p[19]);
vop(p[7], p[11]); vop(p[11], p[13]); vop(p[11], p[12]);
vop.store(dst+j, p[12]);
}
limit = size.width;
}
}
}
}
}