1 均匀成本搜索

均匀成本搜索是迪杰斯特拉算法的变体。这里，我们不是将所有顶点插入到一个优先级队列中，而是只插入源，然后在需要时一个接一个地插入。在每一步中，我们检查项目是否已经在优先级队列中(使用访问数组)。如果是，我们执行减少键，否则我们插入它。 这个 Dijkstra 的变体对于无限图和那些太大而无法在内存中表示的图很有用。均匀成本搜索主要用于人工智能。

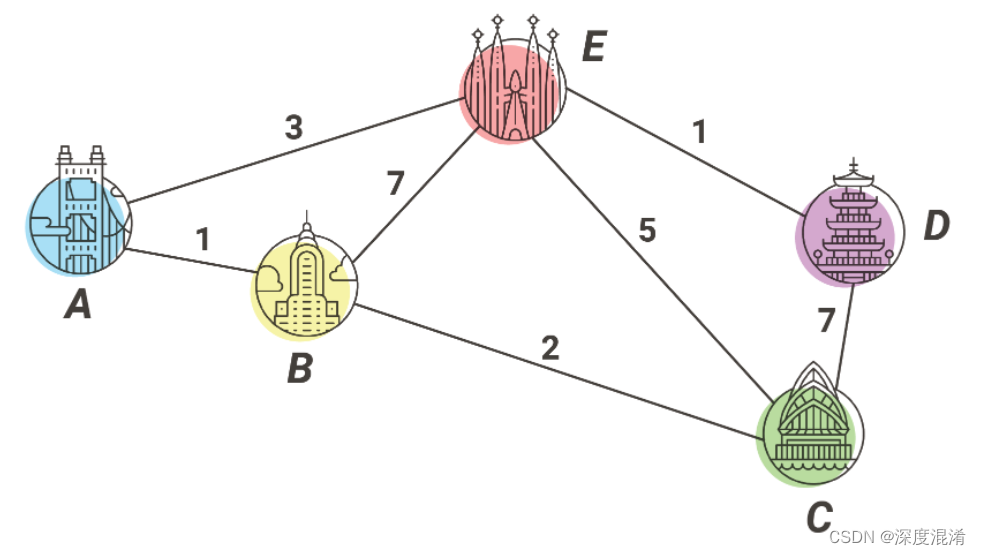
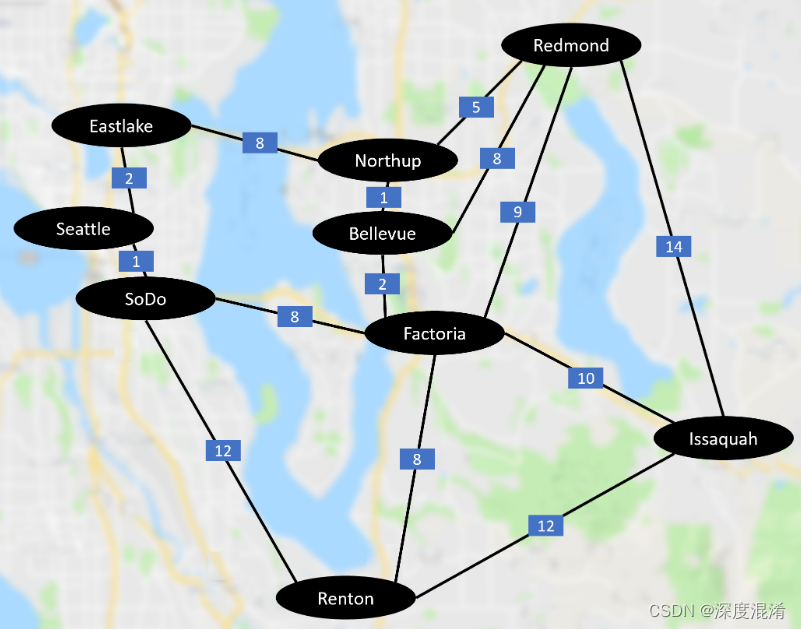
均匀成本搜索类似于迪杰斯特拉算法。在该算法中，从起始状态开始，我们将访问相邻的状态，并将选择代价最小的状态，然后我们将从所有未访问的状态和访问状态的相邻状态中选择下一个代价最小的状态，这样，我们将尝试到达目标状态(注意，我们不会继续通过目标状态的路径)，即使我们到达目标状态，我们也将继续搜索其他可能的路径(如果有多个目标)。我们将保持一个优先级队列，该队列将给出来自被访问状态的所有相邻状态中成本最低的下一个状态。

2 均匀成本搜索源程序

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    public static class LargeGraph
    {
        private static List<List<int>> graph = new List<List<int>>();

        // Tuple 多元组数据
        private static Dictionary<Tuple<int, int>, int> cost = new Dictionary<Tuple<int, int>, int>();

        public static List<int> Uniform_Cost_Search(List<int> goal, int start)
        {
            List<int> answer = new List<int>();

            List<Tuple<int, int>> queue = new List<Tuple<int, int>>();

            for (int i = 0; i < goal.Count; i++)
            {
                answer.Add(int.MaxValue);
            }

            queue.Add(new Tuple<int, int>(0, start));

            Dictionary<int, int> visited = new Dictionary<int, int>();

            int count = 0;

            while (queue.Count > 0)
            {
                Tuple<int, int> q = queue[0];
                Tuple<int, int> p = new Tuple<int, int>(-q.Item1, q.Item2);

                queue.RemoveAt(0);

                if (goal.Contains(p.Item2))
                {
                    int index = goal.IndexOf(p.Item2);

                    if (answer[index] == int.MaxValue)
                    {
                        count++;
                    }
                    if (answer[index] > p.Item1)
                    {
                        answer[index] = p.Item1;
                    }
                    queue.RemoveAt(0);

                    if (count == goal.Count)
                    {
                        return answer;
                    }
                }
                if (!visited.ContainsKey(p.Item2))
                {
                    for (int i = 0; i < graph[p.Item2].Count; i++)
                    {
                        queue.Add(new Tuple<int, int>((p.Item1 + (cost.ContainsKey(new Tuple<int, int>(p.Item2, graph[p.Item2][i])) ? cost[new Tuple<int, int>(p.Item2, graph[p.Item2][i])] : 0)) * -1,
                        graph[p.Item2][i]));
                    }
                }
                visited[p.Item2] = 1;
            }

            return answer;
        }
    }
}

3 代码格式

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    public static class LargeGraph
    {
        private static List<List<int>> graph = new List<List<int>>();

        // Tuple 多元组数据
        private static Dictionary<Tuple<int, int>, int> cost = new Dictionary<Tuple<int, int>, int>();

        public static List<int> Uniform_Cost_Search(List<int> goal, int start)
        {
            List<int> answer = new List<int>();

            List<Tuple<int, int>> queue = new List<Tuple<int, int>>();

            for (int i = 0; i < goal.Count; i++)
            {
                answer.Add(int.MaxValue);
            }

            queue.Add(new Tuple<int, int>(0, start));

            Dictionary<int, int> visited = new Dictionary<int, int>();

            int count = 0;

            while (queue.Count > 0)
            {
                Tuple<int, int> q = queue[0];
                Tuple<int, int> p = new Tuple<int, int>(-q.Item1, q.Item2);

                queue.RemoveAt(0);

                if (goal.Contains(p.Item2))
                {
                    int index = goal.IndexOf(p.Item2);

                    if (answer[index] == int.MaxValue)
                    {
                        count++;
                    }
                    if (answer[index] > p.Item1)
                    {
                        answer[index] = p.Item1;
                    }
                    queue.RemoveAt(0);

                    if (count == goal.Count)
                    {
                        return answer;
                    }
                }
                if (!visited.ContainsKey(p.Item2))
                {
                    for (int i = 0; i < graph[p.Item2].Count; i++)
                    {
                        queue.Add(new Tuple<int, int>((p.Item1 + (cost.ContainsKey(new Tuple<int, int>(p.Item2, graph[p.Item2][i])) ? cost[new Tuple<int, int>(p.Item2, graph[p.Item2][i])] : 0)) * -1,
                        graph[p.Item2][i]));
                    }
                }
                visited[p.Item2] = 1;
            }

            return answer;
        }
    }
}