代码随想录算法训练营第二十四天

news2025/1/4 17:40:08

回溯算法理论基础
- 什么是回溯法
- 回溯法的理解
- 回溯法模板
LeetCode 77.组合
- 题目描述
- 思路
- 参考代码
- 总结
- 优化版本

回溯算法理论基础

文章讲解：代码随想录#回溯算法理论基础
视频讲解：带你学透回溯算法（理论篇）| 回溯法精讲！

什么是回溯法

回溯法也叫做回溯搜索法，是一种搜索的方式。
回溯是递归的副产品，只要有递归就会有回溯。
回溯法的效率并不高，它的本质就是穷举法，有时候也会有剪枝的操作。

有些问题只有通过暴力穷举才能解决，比如可以解决以下问题：
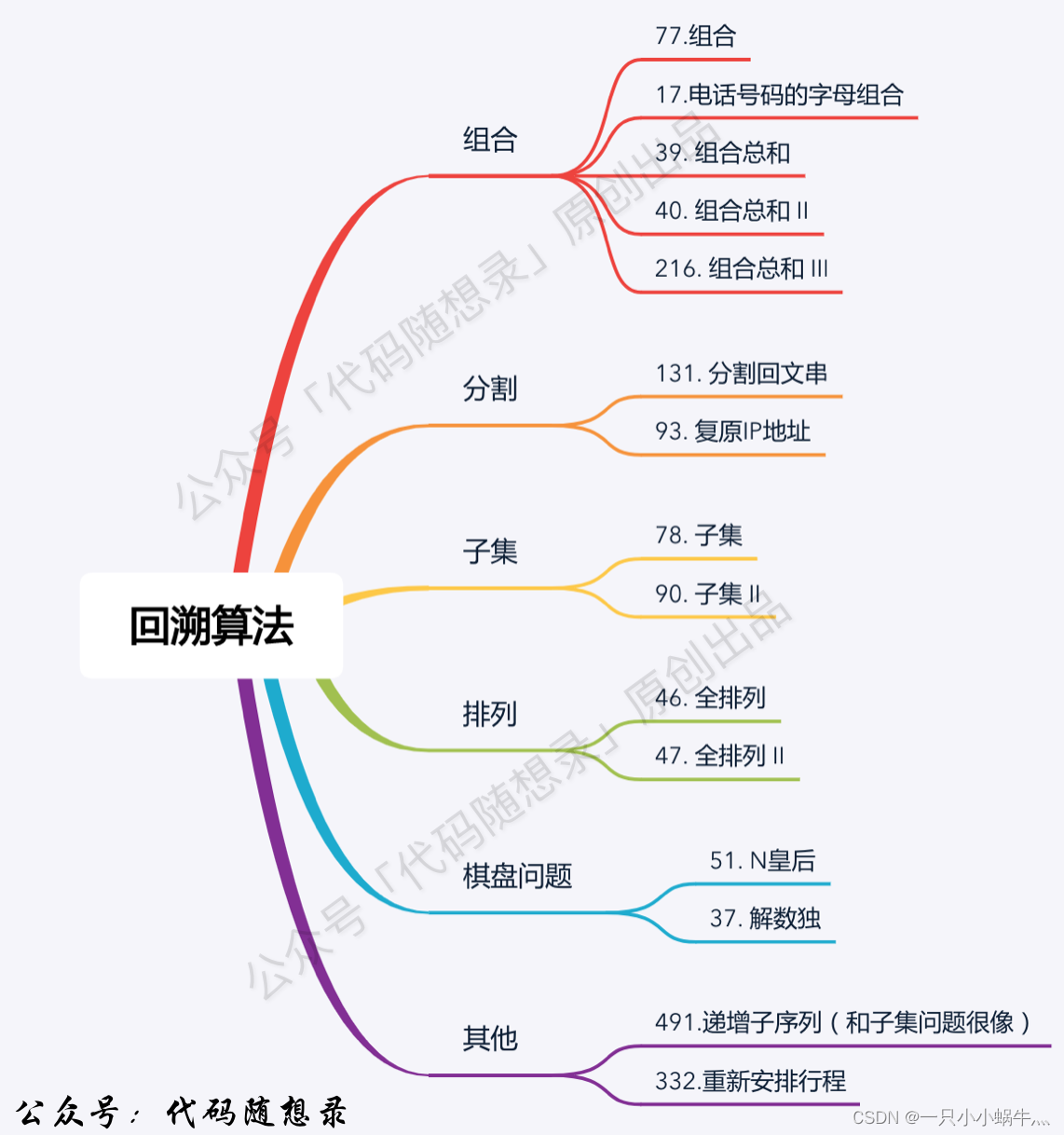
在这里插入图片描述

回溯法的理解

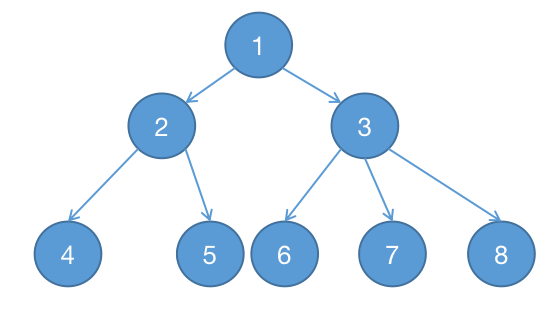
回溯法解决的问题都可以抽象成一个树形结构。
回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树深度。
由于递归有终止条件，所以它是一棵高度有限的树。

回溯法模板

递归有三部曲，同理回溯也有三部曲。

回溯函数体的返回值以及参数
回溯算法中函数返回值一般为void。
参数不能提前确定的，需要在根据处理逻辑来确定参数。
所以回溯函数代码如下

void backtracking(参数)

回溯函数终止条件
一般情况下搜到叶子节点就找到了满足条件的一种解决方法，需要将这个方法保存起来，同时要结束本层递归。

if (终止条件) {
    存放结果;
    return;
}

回溯搜索的遍历过程
回溯一般都是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成了树的深度。

for(选择：本层集合中元素(树中节点孩子的数量就是集合的大小)){
	处理节点;
	backtracking(路径，选择列表); // 继续递归
	回溯处理;
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就会执行多少次。
其实，for循环就是横向遍历，递归就是纵向遍历。

回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

LeetCode 77.组合

题目链接：77.组合
文章讲解：代码随想录#77.组合
视频讲解：带你学透回溯算法-组合问题（对应力扣题目：77.组合）| 回溯法精讲！

题目描述

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

示例1

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例2

输入：n = 1, k = 1
输出：[[1]]

提示

1 <= n <= 20
1 <= k <= n

思路

这是一道经典的回溯题，求的是组合，并非排列。
对于组合，【1，2】和【2，1】是一回事，对于排列【1，2】和【2，1】不相同。
组合是不强调元素顺序的，排列是强调元素顺序。
所以，这道题中某个元素进行过组合后，就需要不能再重复计算了。

那如何使用回溯算法呢？
上面说过回溯的问题都可以抽象成树形结构，盗图说明一下。
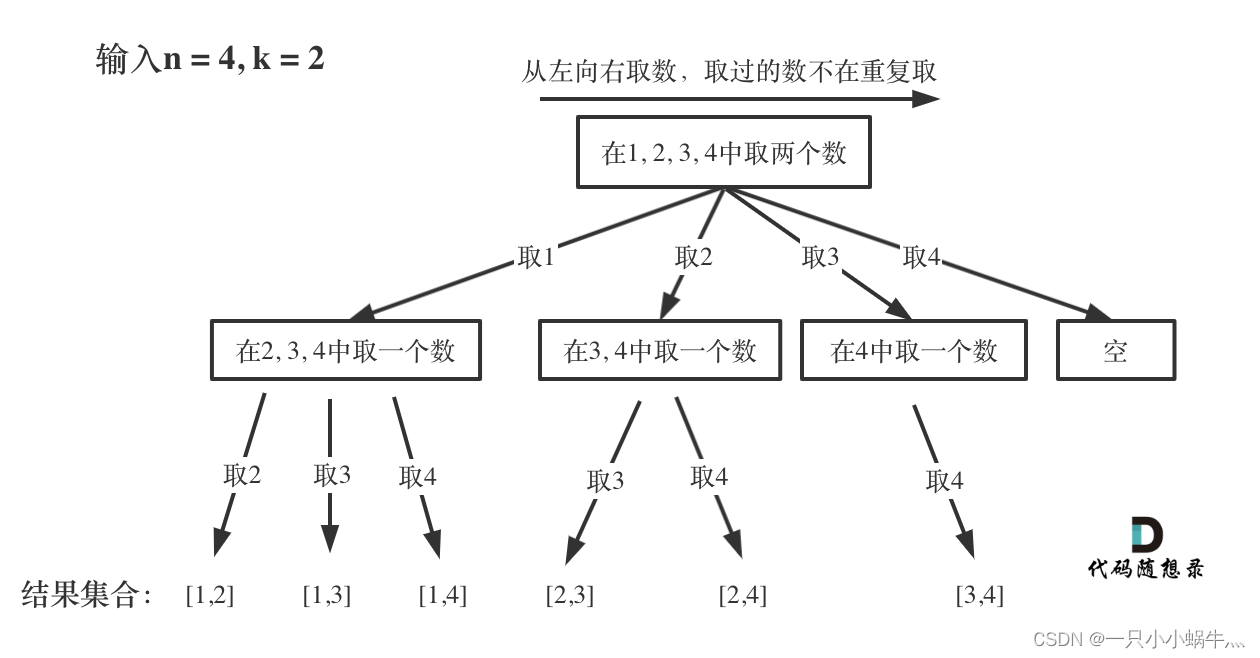
在这里插入图片描述
n相当于树的宽度，k相当于树的深度，每次搜索到叶子节点就表示找到了一个结果。

参考代码

typedef struct {
    int index;
    int num[100];
}Result;

Result result = {0};
int **res = NULL;
int cnt = 0;

void backtracking(int n, int k, int idx)
{
    if (result.index == k) { // 终止条件，当result中已经放入了k个元素时
        res[cnt] = (int*)malloc(k * sizeof(int));
        for(int i = 0; i < k; i++) {
            res[cnt][i] = result.num[i];
        }
        cnt++;
        return;
    }

    for (int i = idx; i <= n; i++) { // 相当于树的横向遍历
        result.num[result.index++] = i; // 处理节点
        backtracking(n, k, i + 1); // 递归遍历下一层
        result.index--; // 回溯
        result.num[result.index] = 0;

    }
}

int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    res = (int**)malloc(10000 * sizeof(int*));

    backtracking(n, k, 1);

    *returnSize = cnt;
    *returnColumnSizes = (int*)malloc(sizeof(int) * cnt); // 需要给returnColumnSizes分配内存
    for (int i = 0; i < cnt; i++) {
        (*returnColumnSizes)[i] = k;
    }
    return res;
}