目录

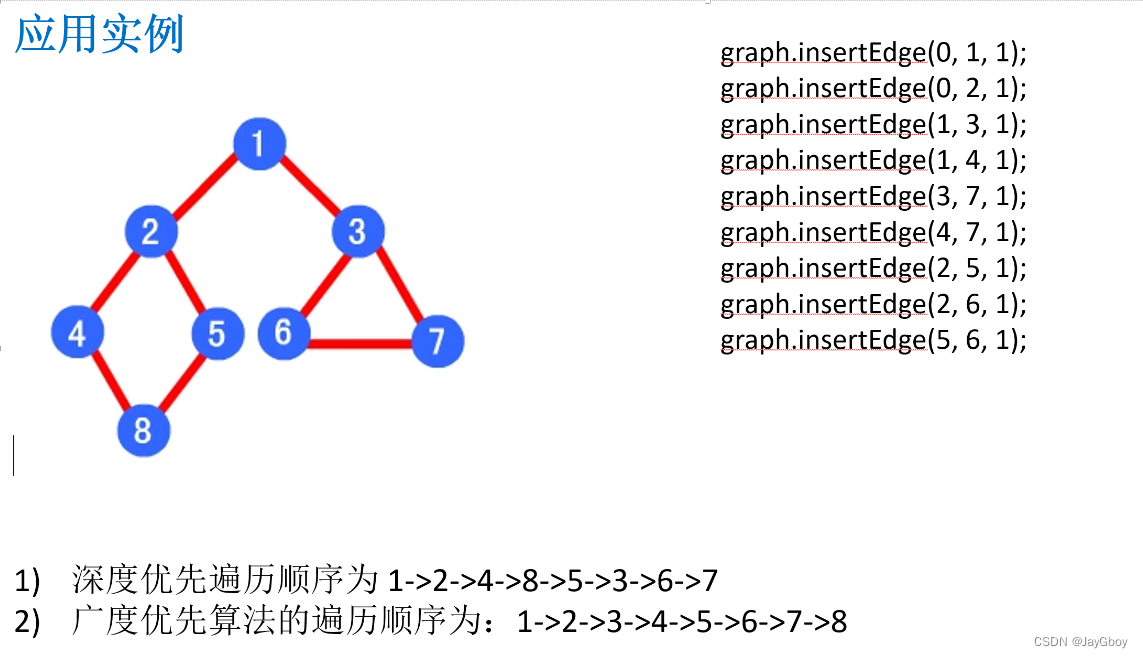
1.KMP算法的介绍

2.next数组

3.总结

---

1.KMP算法的介绍

首先我们会疑惑，什么是KMP算法？这个算法是用来干什么的？

KMP（Knuth-Morris-Pratt）算法是一种用于字符串匹配的经典算法，它的目标是在一个主文本串（text）中查找一个模式串（pattern）的出现位置。KMP 算法通过利用模式串本身的特性，在匹配过程中避免回溯文本串的指针，从而达到快速匹配的目的。

KMP 算法的关键在于构建一个部分匹配表（Partial Match Table），

通常称为「next 数组」。这个表记录了模式串中每个位置对应的最长相同前缀后缀的长度。利用这个表，算法可以在匹配过程中智能地调整模式串的位置，避免不必要的比较，从而提高了匹配效率。

我们可以试想，当我们想将一个模式串遇主串匹配，并且找到模式串在主串中出现的第一个位置，通常我们会想到暴力求解。就是使用两个for循环，第一次for循环从主串的第一个元素开始遍历，当这时这个元素与模式串的第一个元素相同，那么我们就继续比对下一个元素，依次进行来找到模式串在主串出现的第一个元素，但是暴力求解的时间复杂度是（n*m），n是主串的长度，m是模式串的长度。

但是KMP算法可以将时间复杂度缩减到（n+m），大大节省了程序运行时间。

我们现在先来看一下KMP算法是如何匹配字符串，可以将时间复杂度缩减到（n+m）的。

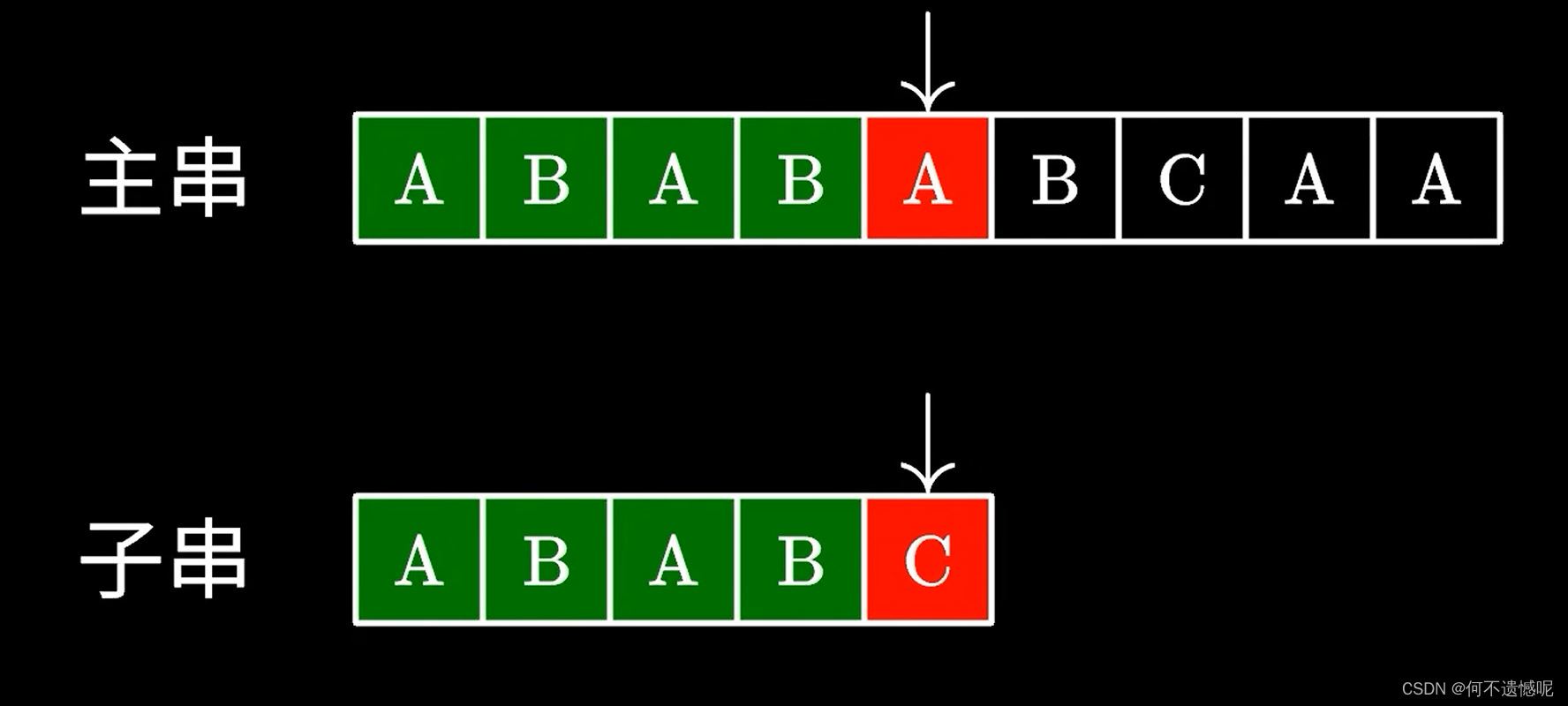面对上面这两个字符串的比对，我们会发现，在第一次比对时，只有最后一个元素不同，按照暴力算法是将子串与主串的第二个元素重新比对，但是KMP算法却不是这样比对，而是直接与主串的第三个元素比对，这时发现成功匹配。

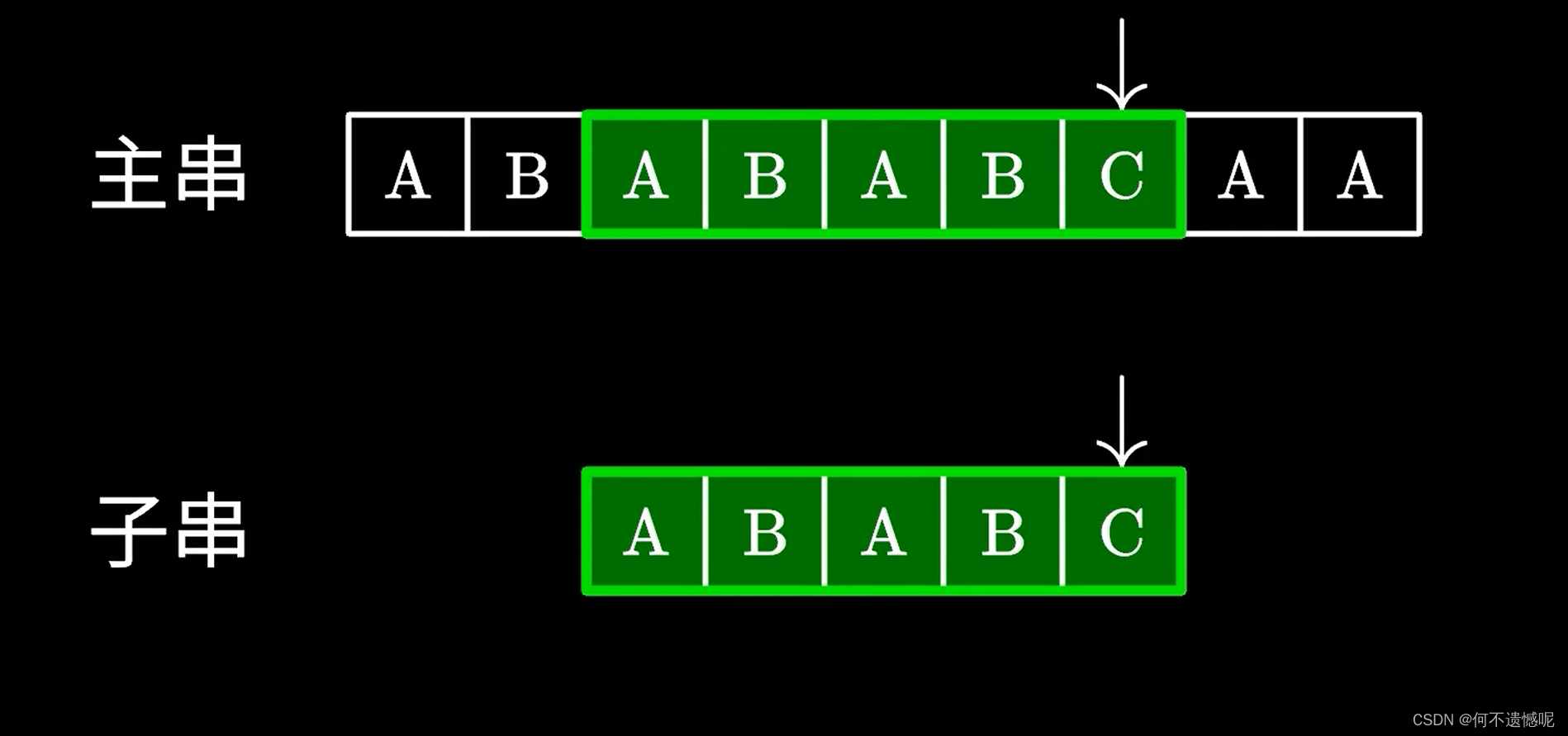
那么我们应该怎么知道该将子串前进几个元素重新与主串比对呢？

这就需要我们引入一个next数组，前进几个元素取决于当出现不匹配的元素的前一个元素的所对应的next数组值。

2.next数组

1.构建部分匹配表（next 数组）：遍历模式串，对每个位置计算最长相同前缀后缀的长度。这个长度表示了在当前位置失配时，应该移动模式串的位置以继续匹配。

那么什么是前后缀数组呢？

首先给出示例字符串：ababcbcab

它的前缀集合：{a,ab,aba,abab,ababc,ababcb,ababcbc,ababcbca}

它的后缀集合：{a,ab,cab,bcab,cbcab,bcbcab,abcbcab,babcbcab}

注意不能算是它本身，不然最长长度一直都是自己了。

看了上面的示例，那么对前后缀有了一个清晰的认识了吧！

这里相同的前后缀是ab，它的长度是2，那么此时的next数组里面是2。

现在给出求next数组的代码：

void get_next() //求出next数组 
{ 
    int i=0,j=-1;
    next1[0]=-1;
    while(i<len2) 
        if(j==-1 || s2[i]==s2[j]) 
            next1[++i]=++j;
        else j=next1[j];
} 

我们现在给出一个示例字符串：ABABACAB

1.第1个元素直接是0。

2.第2个元素的前缀合集合是{A}，后缀是{B}，没有共同，第二个是0。

3.第3个元素的前缀合集合是{A,AB}，后缀是{A,BA}，有相同的"A"，那么是1。

4.第4个元素的前缀合集合是{A,AB,ABA}，后缀是{B,AB,BAB}，相同的是"AB"，那么是2。

5.第5个元素的前缀合集合是{A,AB,ABA,ABAB}，后缀是{A,BA,ABA,BABA}，相同的是"ABA"，那么是3。

6.第6个元素的前缀合集合是{A,AB,ABA,ABAB,ABABA}，后缀是{C,AC,BAC,ABAC,BABAC}，没有相同的，那么是0。

7.第7个元素的前缀合集合是{A,AB,ABA,ABAB,ABABA,ABABAC}，后缀是{A,CA,ACA,BACA,ABACA,BABACA}，相同的是"A",那么是1。

8.第8个元素的前缀合集合是{A,AB,ABA,ABAB,ABABA,ABABAC,ABABACA}，后缀是{B,AB,CAB,ACAB,BACAB,ABACAB,BABACAB}，相同的是"AB",那么是2。

那么我们计算出的next数组是：0 0 1 2 3 0 1 2

现在我们看代码运行结果。

代码计算出来也与我们手算的结果一样。

3.总结

匹配过程：在主文本串中从左往右逐个字符地与模式串进行比较。当发生不匹配时，根据部分匹配表的值来移动模式串的位置，而不是直接回溯到起始位置重新开始比较。

这时我们看看KMP的核心代码：

void KMP() //KMP 
{ 
    int i=0,j=0;//从第一个元素开始匹配 
    while(i<len1) 
    { 
        if(j==-1 || s1[i]==s2[j]) //匹配成功 
            i++,j++;
        else j=next1[j]; //失配 
        if(j==len2)
		{
			cout<<i-len2+1<<endl;//此时i-len2+1为匹配成功的第一个元素位置 
			j=next1[j];//匹配成功，再失配 
		} 
    }  
} 

总的来说，KMP 算法通过预处理模式串构建部分匹配表，然后利用这个表在匹配过程中避免不必要的回溯，从而提高了字符串匹配的效率。

下面我们可以做一道题来巩固我们的学习结果。

P3375 【模板】KMP - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

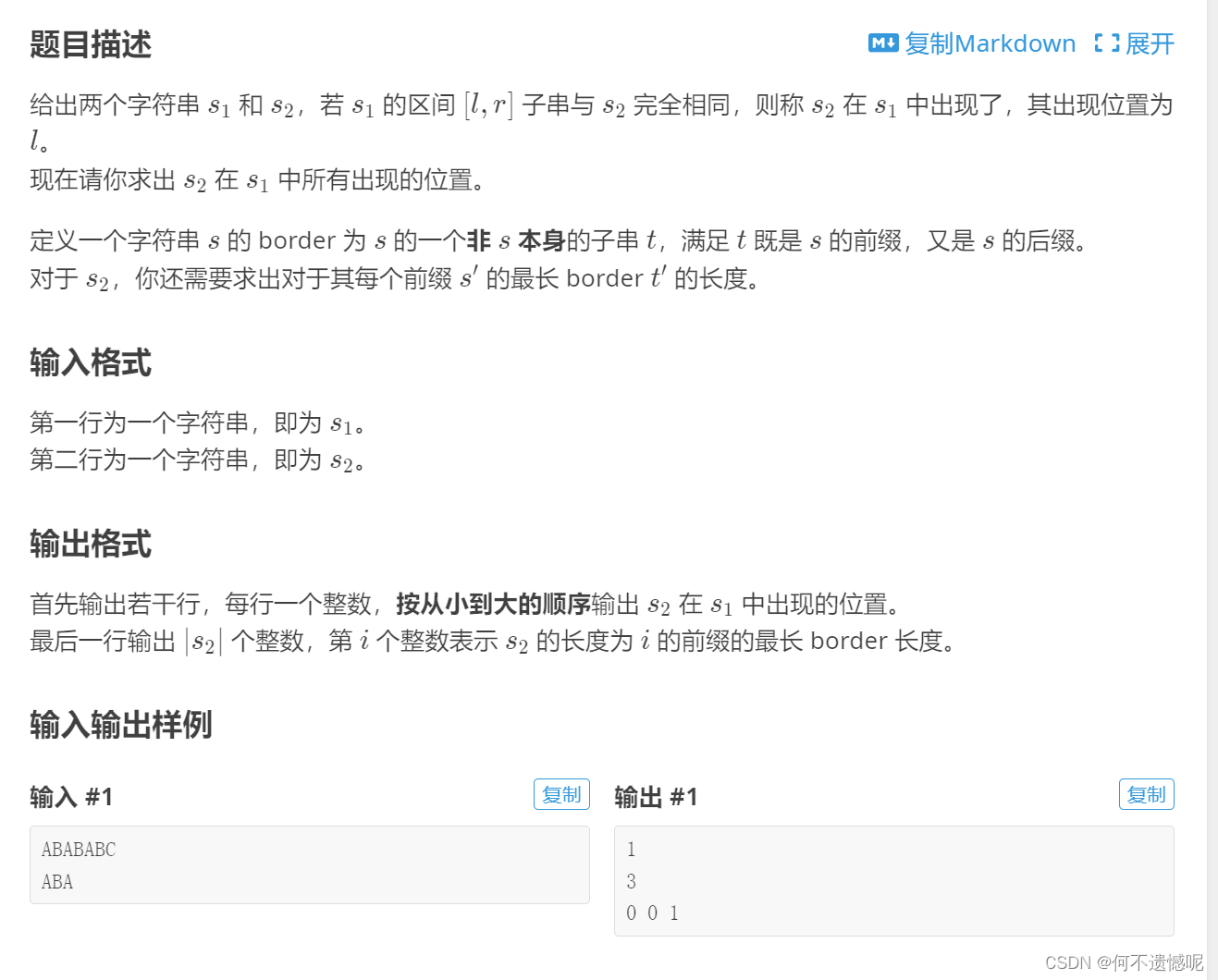
输入数据：

ABABABC
ABA

下面AC完整代码：

#include<bits/stdc++.h>
using namespace std;
int len1,len2;
int next1[1000001];
char s1[1000001];
char s2[1000001];
void get_next() //求出next数组 
{ 
    int i=0,j=-1;
    next1[0]=-1;
    while(i<len2) 
        if(j==-1 || s2[i]==s2[j]) 
            next1[++i]=++j;
        else j=next1[j];
} 
void KMP() //KMP 
{ 
    int i=0,j=0;//从第一个元素开始匹配 
    while(i<len1) 
    { 
        if(j==-1 || s1[i]==s2[j]) //匹配成功 
            i++,j++;
        else j=next1[j]; //失配 
        if(j==len2)
		{
			cout<<i-len2+1<<endl;//此时i-len2+1为匹配成功的第一个元素位置 
			j=next1[j];//匹配成功，再失配 
		} 
    }  
} 
int main(){ 
    cin>>s1>>s2;
    len1=strlen(s1);
    len2=strlen(s2);
    get_next();
    KMP();
    for(int i=1;i<=len2;++i) 
        cout<<next1[i]<<" ";//输出next数组 
    return 0;
}