为什么需要位置表示
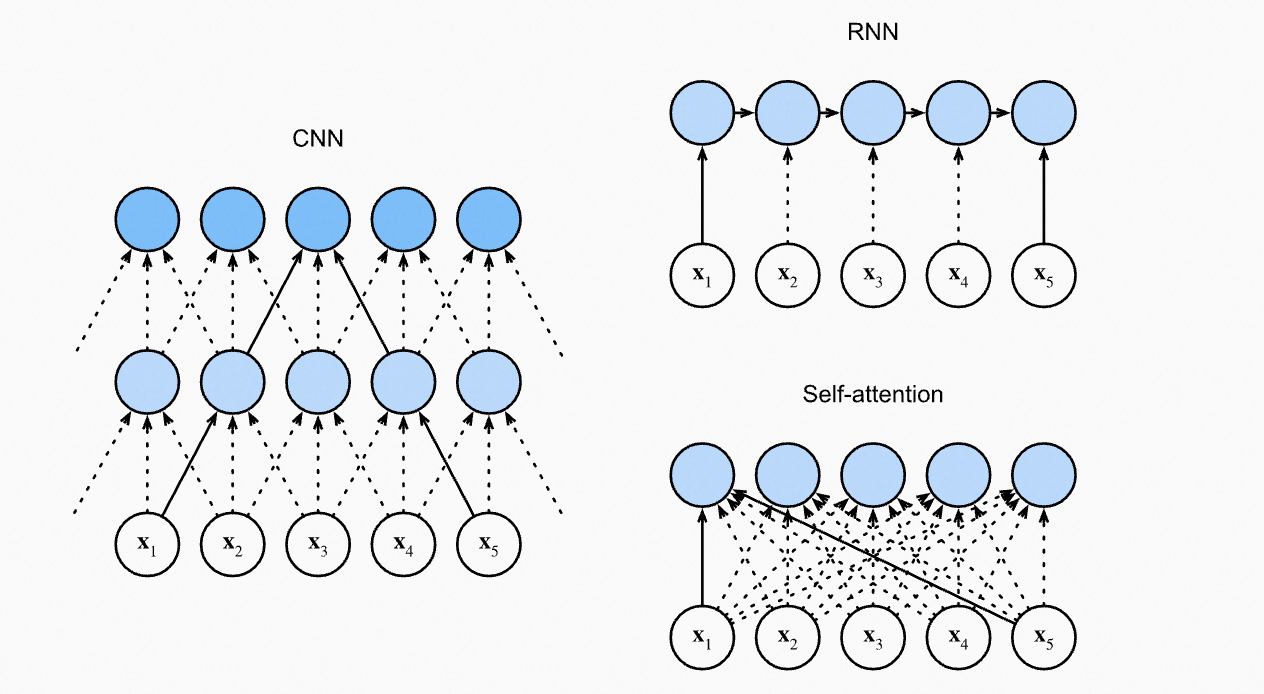
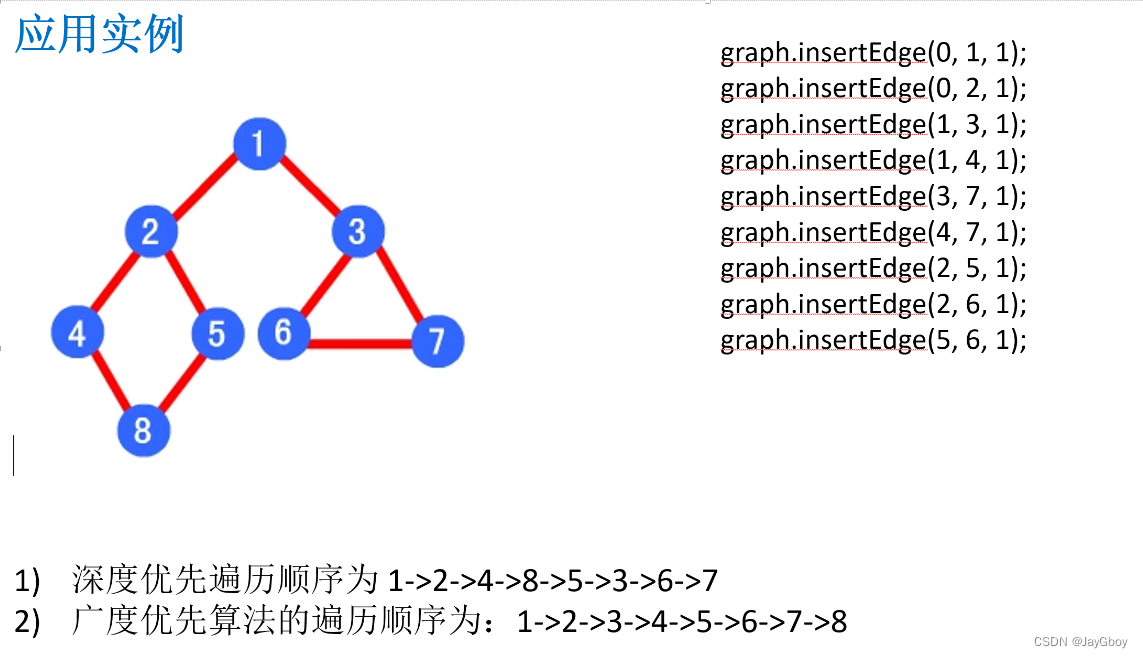
对比CNN、RNN和Self-Attention:
CNN处理相邻窗口的内容;RNN天然是序列操作,考虑了位置先后关系;Self-Attention的计算时是无序的,所以需要位置表示来知道Token之间的位置信息。
绝对位置表示
典型如:Bert/Roberta/GPT2的位置表示,将位置如 0~512 像词一样做embedding,需要训练position向量矩阵

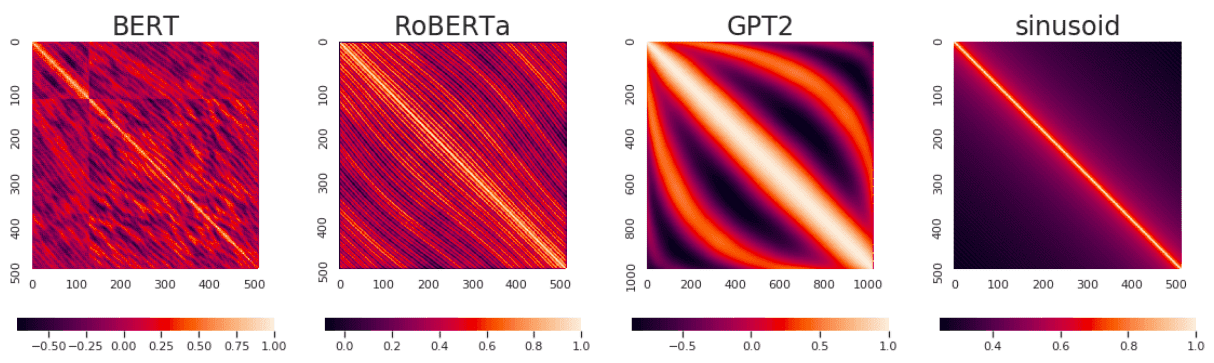
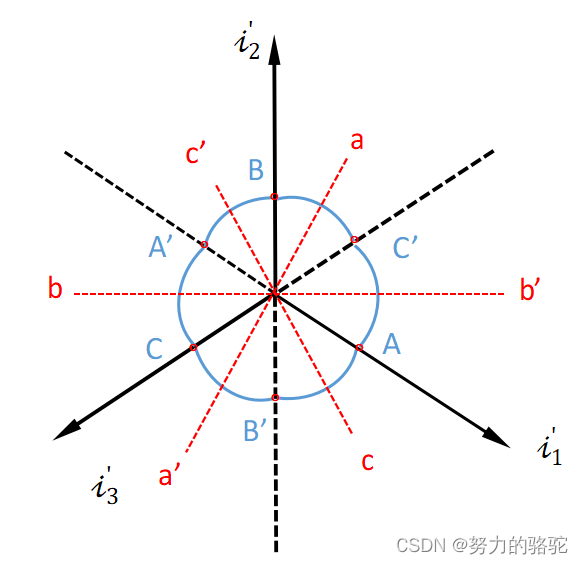
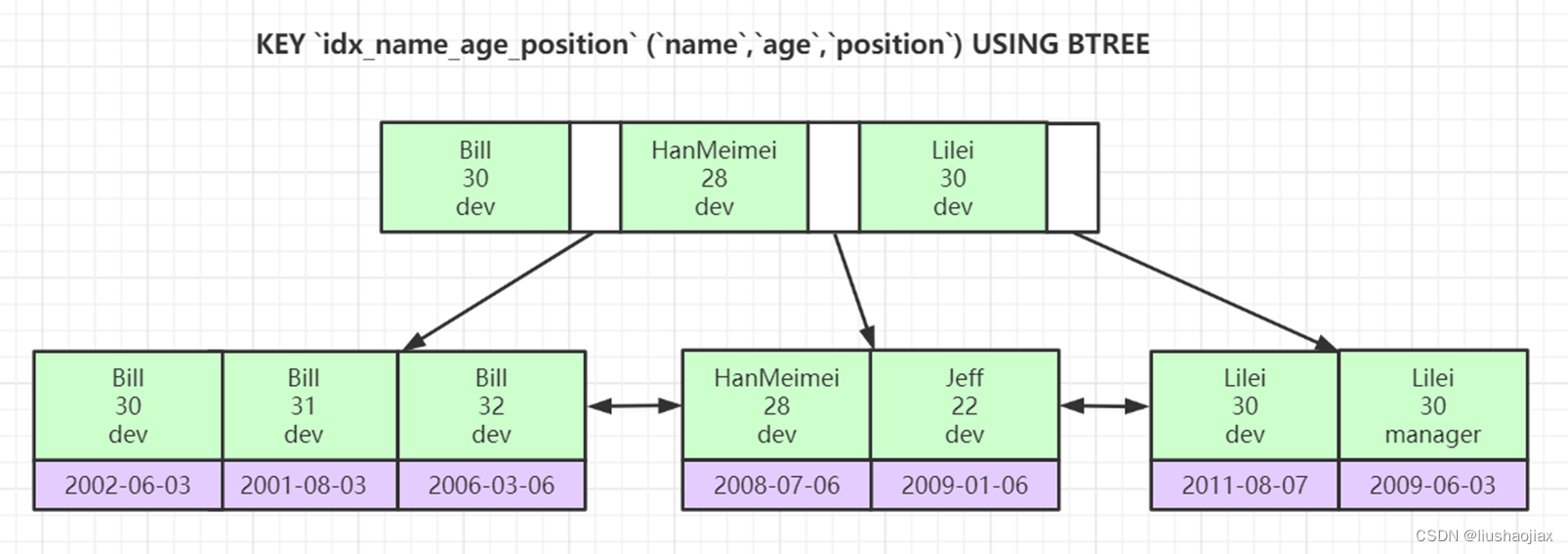
不同模型训练出来的位置表示之间的相似性,对角线是1
优势:简单
劣势:无法处理超出长度的句子,必须截断
相对位置表示
位置n的旋转位置编码(RoPE),本质上就是数字n的β进制编码!- 苏剑林
为什么需要进制编码?我们先看进制编码的格式:
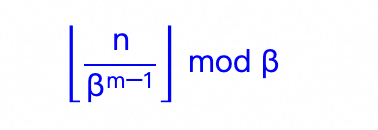
我们再回到RoPE的公式:pos是位置,i是表示向量的维度
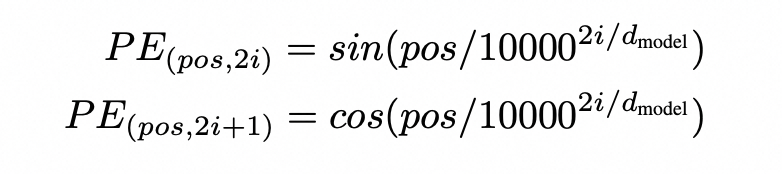
令 \beta=10000^2,那么RoPE就是下面这种表示,也就是完整的进制编码表示:
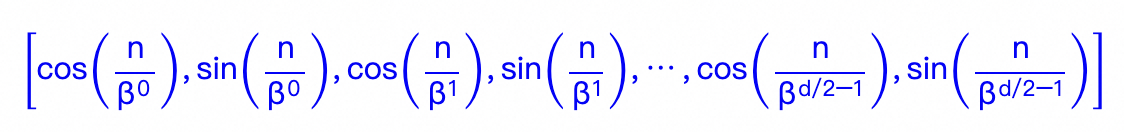
我们再看下位置表示的可视化,发现当表示向量的维度上升,曲线更加稠密;
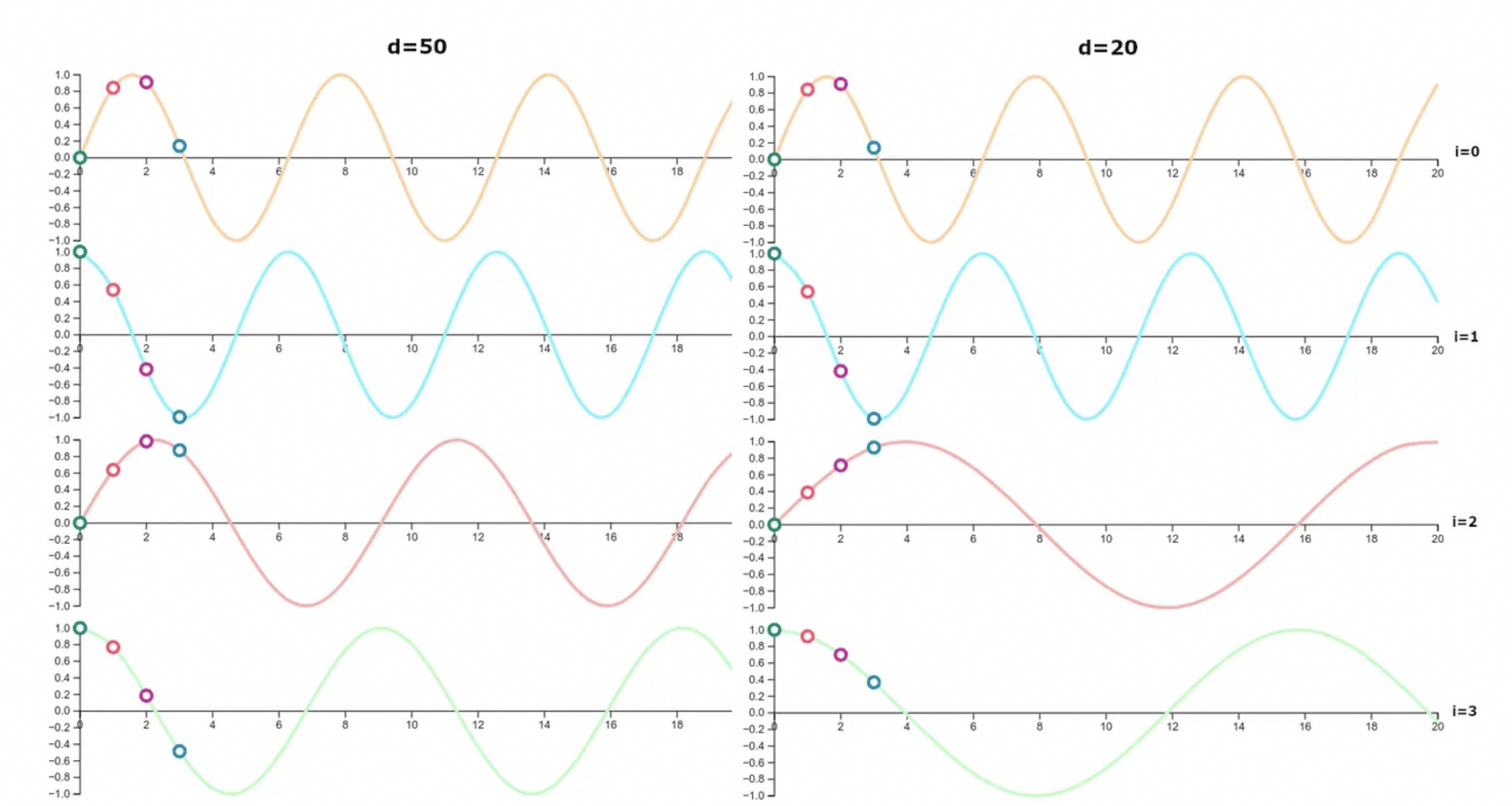
为什么要用周期进制表示:
-
进制在表示相对位置时和绝对位置表示是一样的效果,如「我们知道10的相邻数据是9和11」
-
周期进制表示方式,更加的稠密;就像10/16进制一样,进制越高,表示信息越大
-
周期进制可以做推理:假设我们已经学习过0~200的表示,那么对于200~299,直接就知道他们的位置和关系;甚至于200~999也是可以直接知道含义的
如何扩展位置表示
直接外推
如果我们学习过position 在0~200之间的表示,那么对于200~299的长度,可以直接扩展,甚至 200~999的位置表示,也可以直接外推。但是如果是1000~以上的范围,那么效果就不好了,因为千位的维度没有训练过。
优点是:在预留的维度上,是可以直接外推,不需要训练的;
缺点:超出范围的,性能下降极大
线性内插
如果我们学习过position 在0~200之间的表示,我们需要表示更长,一种是我们每隔0.5就做一个表示,这样表示能力扩展到 0~400了,这样还是保持学习范围之内,但是问题是表示更加拥挤,当处理范围进一步增大时,相邻差异则更小,这样位置表示的作用就减弱了。
优点是:原则上可以无限内插下去
缺点:差异小了,PE的效果降低
Neural Tangent Kernel—NTK-aware
内插 + 外插叠加:在低位的时候,基本和原来一致,不影响原始表示,这个就是外插;在高位的时候,往里面内插,虽然信息降低,但是也可以表示