一、什么是堆?
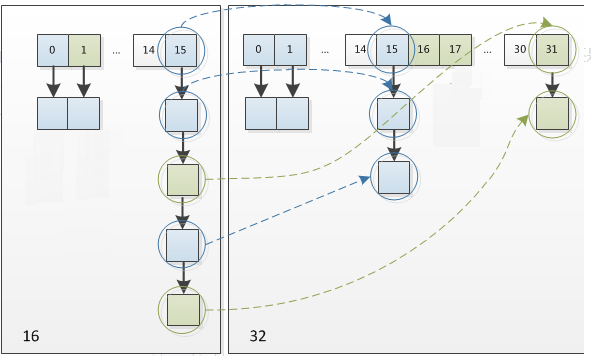
堆是将数组看作一颗完全二叉树
大堆:任意一个父亲大于等于孩子

小堆:任意一个父亲小于等于孩子
有序数组一定是堆
但是堆不一定有序
注意:此“堆”是一个数据结构,用来表示完全二叉树
还有另外一个“堆”,是内存区域的划分,是我们动态申请内存的内存区域,属于操作系统的概念
属于不同学科中的同名概念而已
二、堆的应用场景
1、堆排序,O(N*logN)(在一堆数据中找到某个数据)
2、top K问题(一堆数据中找到前K个最大或者最小的数据)
堆二叉树插入值:向上调整,和其祖先进行比较
数组可以建立堆的核心是,利用完全二叉树的父子和左右孩子下标的关系特点
同时,在实际的物理存储中是数组,但是想象中,我们处理的是逻辑结构中的完全二叉树
堆的删除默认是删除堆顶
向下调整算法:删除堆顶元素,数组尾和堆顶元素交换,删除尾巴,然后交换过去的堆顶又向下调整(这里要注意数组越界的问题)
fscanf:将数据流(一般是从文件中读取,就是文件指针)中的数据放到对应格式的位置上去
fscanf(文件指针,格式%d,写入的位置&x);
fprintf();写文件
(free就算传入的是空,也没有问题,因为free对空进行了检查)
正数数据类型:size_t
调试:结构体内部情况struct.a,8(这个8代表的是a中的8个数据值)
三、堆的基本操作源代码
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
//交换函数
void Swap(HPDataType* a, HPDataType* b);
//向下调整
void AdujustDown(HPDataType* a, int size,int parent);
//向上调整
void AdujustUp( HPDataType* a, int child);
//初始化堆
void HeapInit(Heap* hp);
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//堆排序
void HeapSort(int* a, int n);#include"Heap.h"
//大堆
//初始化堆
void HeapInit(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
void Swap(HPDataType* a, HPDataType*b)
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
//向下调整
void AdujustDown(HPDataType* a, int size, int parent)
{
//假设左孩子比较大
int child = parent * 2 + 1;
while(child < size)
{
if (child + 1 < size && a[child + 1] > a[child])
{
//更改比较大孩子
++child;
}
if (a[parent] < a[child])
{
Swap(&a[parent],&a[child]);
parent = child;//更新父节点
child = parent * +1;//依旧将孩子更新为左孩子
}
else
{
break;
}
}
}
//向上调整
void AdujustUp(HPDataType* a, int child)
{
//从孩子位置开始向上调整
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child],&a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (tmp ==NULL)
{
perror("malloc fail");
exit(-1);
hp->_a = tmp;
hp->_size = n;
hp->_capacity = n;
}
//每插入一个值,就调整一个值
for (int i = 0;i<n;++i)
{
AdujustUp(a,i);
}
for (int i = 0;i<n;++i)
{
HeapPush(&hp->_a,a[i]);
}
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_capacity = 0;
hp->_size = 0;
printf("Destory Succeed\n");
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
//扩容
if (hp->_capacity == hp->_size)
{
int newCapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->_a,sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail ");
exit(-1);
}
hp->_a = tmp;
hp->_capacity = newCapacity;
}
hp->_a[hp->_size] = x;
hp->_size++;
//插入后向上调整
AdujustUp(hp->_a,hp->_size - 1);
}
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
//先交换,再向下调整
Swap(&hp->_a[0],&hp->_a[hp->_size - 1]);
hp->_size--;
AdujustDown(hp->_a,hp->_size,0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
return hp->_size == 0;
}
//交换数据,对剩下的数据进行向调整
void HeapSort(int* a, int n)
{
//for (int i = 0;i<n;++i)
//{
// AdujustUp(a,i);
//}
// O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdujustDown(a, n, i);
}
while(n>0)
{
Swap(&a[n - 1], &a[0]);
AdujustDown(a, n-1, 0);
n--;
}
}
、
#include"Heap.h"
int main()
{
int a[] = { 0,3,5,7,2,9,4,4,6 };
int n = sizeof(a) / sizeof(int);
HeapSort(&a,n);
for (int i = 0; i < n; ++i)
{
printf("%d ",a[i]);
}
return 0;
}