说明:这是一个机器学习实战项目(附带数据+代码+文档+视频讲解),如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景
霍尔特季节性平滑模型是指数平滑技术的一种扩展形式,由E. S. Holt和P. R. Winters分别独立提出并进一步发展。该模型旨在处理具有趋势和季节性的时间序列数据,它结合了霍尔特线性趋势指数平滑(Holt's Linear Trend Method)以及对季节性成分的估计。
在霍尔特-温特斯季节性指数平滑模型中,包含了三个基本成分:
水平(Level):代表时间序列的基本水平或平均值。
趋势(Trend):描述时间序列中的长期上升或下降趋势。
季节性(Seasonality):反映周期性的波动,如每个季度、每月或每周的变化规律。
本项目通过Holt算法来构建时间序列分析霍尔特季节性平滑模型。
2.数据获取
本次建模数据来源于网络(本项目撰写人整理而成),数据项统计如下:
| 编号 | 变量名称 | 描述 |
| 1 | DATE | |
| 2 | y |
数据详情如下(部分展示):
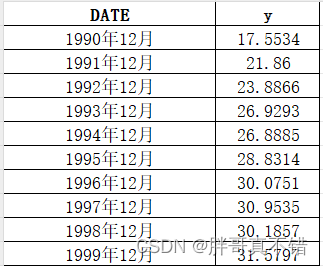
3.数据预处理
3.1 用Pandas工具查看数据
使用Pandas工具的head()方法查看前五行数据:

关键代码:

3.2 数据缺失查看
使用Pandas工具的info()方法查看数据信息:
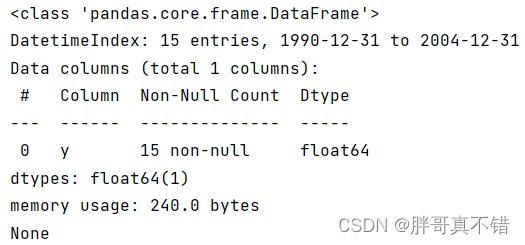
从上图可以看到,总共有1个变量,数据中无缺失值,共15条数据。
关键代码:

3.3 数据描述性统计
通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。
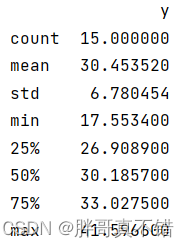
关键代码如下:

4.探索性数据分析
4.1 变量直方图
用Matplotlib工具的hist()方法绘制直方图:
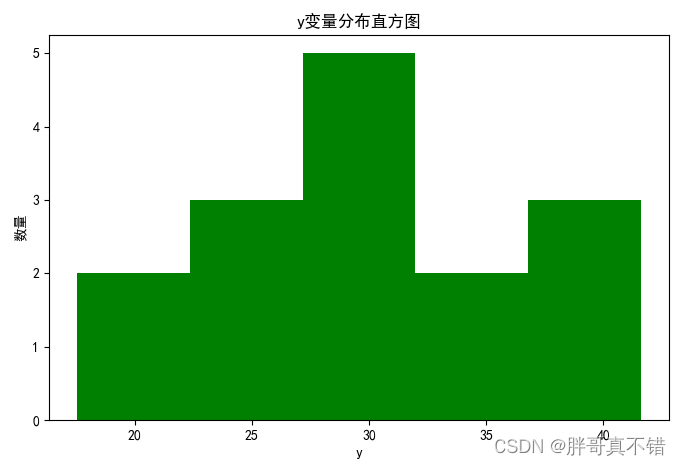
从上图可以看到,变量主要集中在20~40之间。
4.2 折线图

从上图中可以看到,数据呈逐步上升趋势。
5.构建霍尔特季节性平滑模型
主要使用Holt算法,用于时间序列分析霍尔特季节性平滑模型。
5.1 构建模型
| 编号 | 模型名称 | 参数 |
| 1 | 霍尔特季节性平滑模型 | initialization_method="estimated" |
| 2 | smoothing_level=0.8 | |
| 3 | smoothing_trend=0.2 | |
| 4 | optimized=False |
5.2 模型摘要信息一
为指定指数参数的模型摘要信息:
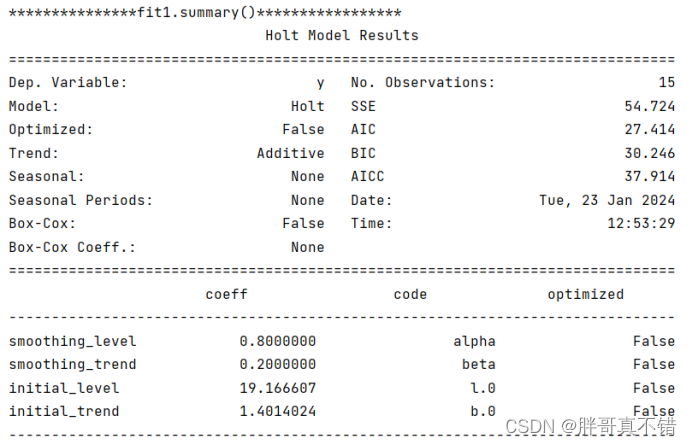
5.3 模型摘要信息二
指定指数参数的模型摘要信息:

5.4 模型摘要信息三
采用阻尼趋势的模型摘要信息:

6.模型评估
6.1 真实值与预测值比对图
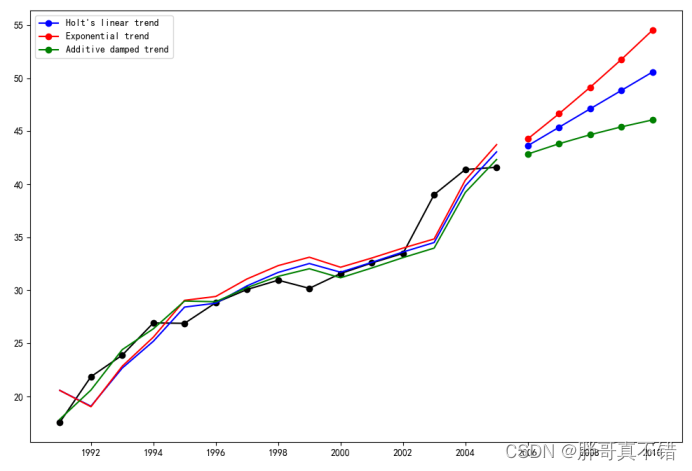
7.结论与展望
综上所述,本文采用了Holt算法来构建时间序列分析霍尔特季节性平滑模型,最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。
# 本次机器学习项目实战所需的资料,项目资源如下:
# 项目说明:
# 获取方式一:
# 项目实战合集导航:
https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2
# 获取方式二:
链接:https://pan.baidu.com/s/16X-Ia86L4XvvXhc-4NxDCQ
提取码:rsy6