碳化硅模块使用烧结银双面散热DSC封装的优势与实现方法
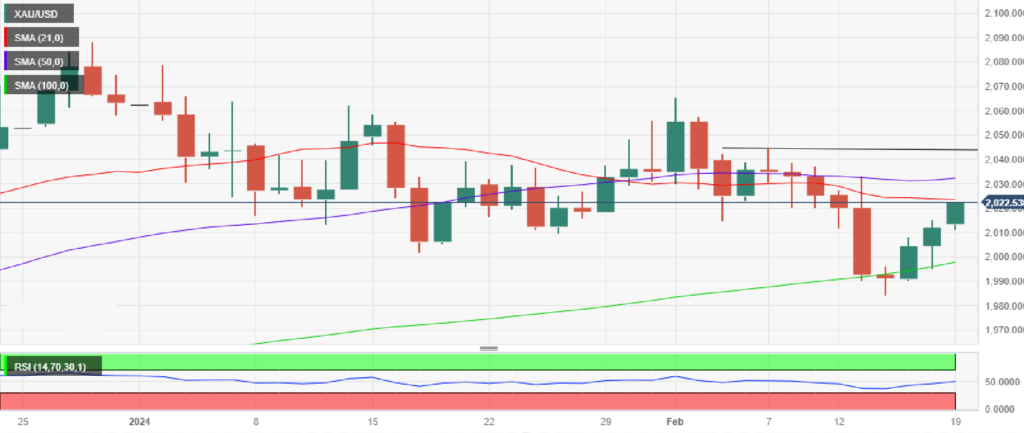
新能源车的大多数最先进 (SOTA) 电动汽车的牵引逆变器体积功率密度范围从基于 SSC-IGBT 的逆变器的 <10 kW/L 到基于 SSC-SiC 的逆变器的约 25 kW/L。100 kW/L 代表了这一关键指标的巨大飞跃。
当然,随着新能源车碳化硅的广泛应用,散热问题成为制约发展的瓶颈问题,双面散热方案被提到日程上来了。
一 碳化硅双面散热的优势
双面散热 SiC 模块方面所做的工作,与传统的相比,该模块可以显示牵引逆变器性能的巨大改进单侧冷却模块。利用双面散热模块改进的性能,可以显著减少SiC芯片数量,从而带来功率密度和成本优势。
1碳化硅芯片数量减少:从24颗减少到12颗或者16颗;
2热阻降低30% 以上;
3电感降低70%:由于不使用铜键合线;
4面积缩小50%;
5综合以上因素,可以提高接近40%的功率密度。
二 碳化硅双面散热的实现方法
碳化硅双面散热 DSC来说,碳化硅芯片通常夹在两个导电导热基板之间。以前的顶部连接方法使用覆盖器件区域一部分的短金属柱,已经尝试了许多材料用于金属柱,例如铜、钼等材料。
对于背面芯片来说,烧结银AS9377比焊接有在连接方面有优势,无压烧结银形成的致密银层具有更高的导热性和导电性以及更高的可靠性。使用无压烧结银膏的一个关键优点是:顶部接触的散热系统形成过程中很容易变形,从而适应几何变化,例如基板厚度的差异。
与用于芯片连接的其他焊料相比,烧结银的许多优点现在也转移到了顶部连接,以及低弹性模量的优点,因此比铜或钼柱有更低的机电应力。
三用于碳化硅芯片焊接的无压纳米烧结银
烧结银AS9377在 260°C 或更低的温度下使用固态扩散,可以在没有压力辅助的情况下达到高达50MPA的剪切强度和280W/M.K的导热率。
银烧结比传统焊接方法具有多种优势。比如低温固化高温服役;导热系数高;剪切强度大;环保无铅;性能可靠等优势。
结论
双面散热的功率模块封装的创新可以提高功率密度并减少 SiC 和等材料,从而在电动汽车应用中实现更低的成本和更可持续的功率转换。
本文介绍的使用无压烧结银AS9377的创新的碳化硅双面散热 DSC 方法可以成为用于提高电动汽车性能的众多解决方案之一。