- 周一,金价在本周初延续了其复苏模式;
- 随着投资者重新评估美联储降息押注,美元跟随美债收益率走软;
- 黄金买家需要突破21日移动均线2025美元,RSI指数稳定在50以下;
随着买家将上周的复苏模式延续到周一,黄金价格在新的一周走高。金价的上行轨迹受到美元普遍走软的推动,在市场情绪好坏参半的情况下,美元跟随美债收益率走低。
中国交易员在为期一周的农历新年假期后满怀乐观地重返市场,但亚洲其它股市交易谨慎。投资者重新评估美联储降息预期,尤其是在美国CPI和PPI数据超出预期之后,这有助于将他们对美联储3月至6月降息的预期推后。CME的Fed Watch Tool显示,市场目前预计6月份降息的可能性为77%。
尽管市场对美联储降息的预期比此前预期的要晚,但在美元普遍疲软的情况下,非收益黄金价格仍保持弹性,恢复了复苏势头。美元在新一周伊始仍处于守势,因交易商在周三美联储2月会议纪要公布前重新调整仓位。此外,美国市场周一因纪念总统日而放假,美元受风险情绪支配。
此外,金价正在利用美债收益率的低迷表现和中东地缘政治紧张局势。与此同时,对全球经济增长的担忧也继续成为传统避险资产金价的推动力。上周,英国和日本的GDP数据显示,在连续两个季度出现负增长后,这两个经济体都陷入了技术性衰退。
展望未来,金价可能会守住自两个月低点1984美元的升势,在假日交易清淡的情况下,不排除出现夸张的走势。本周的关键焦点仍然是周三的美联储会议纪要和周四的美国标准普尔全球商业PMI数据。
黄金技术分析
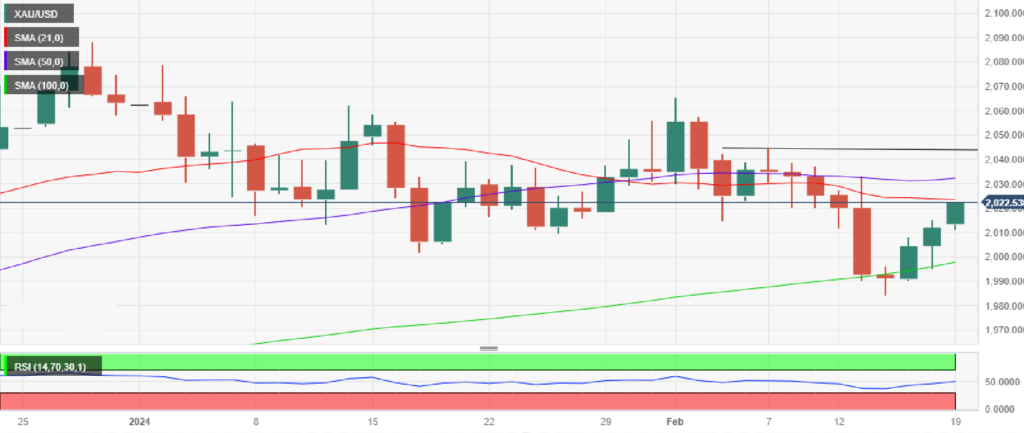
从日线图上可以看出,黄金价格需要在21日简单移动平均线上方得到接受,目前日收盘价为2025美元,以延续复苏。14日RSI也在遵循恢复模式,测试上行的中线。如果RSI指标能够持续突破中线,那么趋势可能会朝着有利于黄金买家的方向转变。下一个上行障碍见于50日移动均线2032美元,如果21日移动均线2025美元被令人信服地突破的话。
进一步看,如果金价看向2050美元的心理障碍,2月7日的高点2044美元将测试看跌承诺。
在下行方面,如果金价跌破21日移动均线,可能会吸引黄金卖家,即时支撑位见于日低点2011美元。如果后者让步,将有可能重新测试2000美元的门槛。黄金买家的最后一道防线将是100日移动均线1998美元,这是上周金价的防线。