1. 模型背景  

    由于可转债自身的属性较多，因此对其定价的难度也会加大，在诸多影响因素中，未来的股价占比最高。由于股价的不可预测性，导致了可转债的定价在实际交易中作用非常有限。随着可转债发行数量和规模的增大，越来越多的机构参与到其中，这也使得越来越多的人开始研究可转债定价，可转债的投机属性降低。随着量化投资的火爆，越来越多的可转债影响因素被标准化，推动了可转债模型定价的迭代的发展。基于市场扩容和技术进步，可转债定价有效性在逐渐加大。目前常见的可转债估值模型有3种：BS模型，二叉树模型，蒙特卡罗模型。本文主要分享二叉树模型的估值逻辑，并复现其代码。

2. 模型公式

3. 模型代码

import numpy as np


class Convertible_Bond(object):
    def __init__(self, T, vol, market, st, rate, r, coupon, r_, dt, up, down, lp):
        self.T = T  # 期限
        self.vol = vol  # 波动率
        self.market = market  # 面值
        self.st = st  # 股票价格
        self.rate = rate  # 转换比率
        self.r = r  # 无风险利率
        self.coupon = coupon  # 票息
        self.r_ = r_  # 信用利差
        self.dt = dt  # 赎回间隔
        self.up = up  # 上涨空间
        self.down = down  # 下跌空间
        self.lp = lp  # 赎回价格

    # 计算风险中性概率
    def risk_p(self):
        a = np.e ** (self.r * self.dt)
        return (a - self.down) / (self.up - self.down)

    # 计算到期价值
    def expire_value(self, expire_price):
        # expire_price:到期股票价格
        # 计算到期转换价值
        change_value = expire_price * self.rate + self.market * self.coupon
        # 计算含票息的价值
        coupon_value = self.market * (1 + self.coupon)
        V = max(change_value, coupon_value)
        return V

    # 计算每一个节点的连续价值
    def continuous_value(self, expire_up, expire_down):
        # expire_down:下一节点下跌对应的可转债到期价值
        # expire_up:下一节点上涨对应的可转债到期价值
        b = np.e ** (-(self.r + self.r_) * self.dt)
        risk_p = self.risk_p()
        coupon_v = self.market * self.coupon
        H = b * (risk_p * expire_up + (1 - risk_p) * expire_down) + coupon_v
        return H

    # 计算当前的节点价值
    def really_value(self, expire_price, H):
        # 计算提前兑付值，假设在赎回时获得票息收入
        C = self.market * self.coupon
        K = self.market + C
        V = max(self.rate * expire_price + C, min(H, K))
        return V

4. 模型实例 

 某可赎回可转债要素如下：（为简化起见，模型暂不考虑部分可转债的特性，使用两步长的最基础的可转债作为案例。）

可赎回-可转债要素
期限	2年	波动率	20%
面值	100	股票价格	100
转换比例	0.8	利率	3%
票息率	3%	信用利差	1%
赎回条款	只在第一年	上涨比例	1.2214
赎回价格	100	下跌比例	0.8187

 首先，对函数进行传参，同时计算s1到s5的值：

if __name__ == '__main__':
    T, vol, market, st, rate, r = 2, 0.2, 100, 100, 0.8, 0.03
    coupon, r_, dt, up, down, lp = 0.03, 0.01, 1, 1.2214, 0.8187, 100
    model = Convertible_Bond( T, vol, market, st, rate,
                              r, coupon, r_, dt, up, down, lp)
    # 分别计算股票s1,到s5的值
    s1 = round(st*up,2)
    s2 = round(st*down,2)
    s3 = round(s1*up,2)
    s4 = round(s1*down,2)
    s5 = round(s2*down,2)

计算得到的结果为：

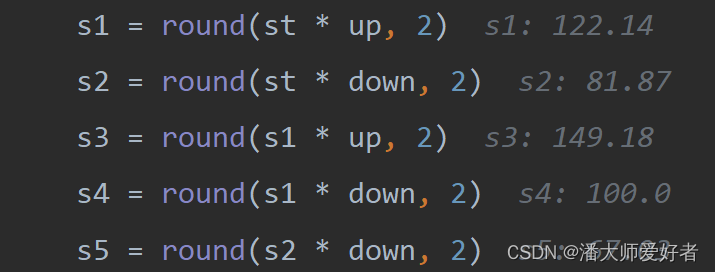
然后，根据 s3,s4,s5的值可以计算出对应节点债券的到期价值：

接下来，根据b3到b5的到期价值，计算b1,b2节点上的连续价值H1,H2：

 随后，考虑可赎回性，根据s1,s2和H1，H2,计算b1,b2节点上的 节点价值1，V2：

紧接着，使用V1和V2的 值计算当前节点的连续价值H，根据H和s1计算当前节点可赎回债券的估值V：

本章节的完整代码为：

if __name__ == '__main__':
    T, vol, market, st, rate, r = 2, 0.2, 100, 100, 0.8, 0.03
    coupon, r_, dt, up, down, lp = 0.03, 0.01, 1, 1.2214, 0.8187, 100
    model = Convertible_Bond(T, vol, market, st, rate,
                             r, coupon, r_, dt, up, down, lp)
    # 分别计算股票s1,到s5的值
    s1 = round(st * up, 2)
    s2 = round(st * down, 2)
    s3 = round(s1 * up, 2)
    s4 = round(s1 * down, 2)
    s5 = round(s2 * down, 2)

    # 计算债券b3,b4,b5的值
    b3 = round(model.expire_value(s3), 2)
    b4 = round(model.expire_value(s4), 2)
    b5 = round(model.expire_value(s5), 2)

    # 计算H1和H2的值
    H1 = round(model.continuous_value(b3, b4), 2)
    H2 = round(model.continuous_value(b4, b5), 2)

    # 计算b1,b2节点上的节点价值
    V1 = model.really_value(s1, H1)
    V2 = model.really_value(s2, H2)

    # 计算当前节点的连续价值H
    H = round(model.continuous_value(V1, V2), 2)
    # 计算当前节点可转债的估值
    V = model.really_value(st, H)

 本期分享结束，有何问题欢迎随时交流。