C++ 离散化算法（详解）+ 例题

news2025/1/20 16:59:21

1、性质

把无限空间中有限的个体映射到有限的空间中去，以此提高算法的空间效率。通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的压缩。
适用范围：数的跨度很大，用的数很稀疏
例如：值域：1~10^9，个数：10^5，值域很大，但是用到个数相对很少，这个时候就可以离散化
比如：将
a[i] : 1 3 100 2000 50000//这里需要注意可以离散化的前提是数组元素必须是有序的
  i  : 0 1  2    3    4  //上面数字映射（离散化）后对应的下标

2、实现方式

我觉得离散化（映射）最大的难点是前后的映射关系，如何能够将不连续的点映射到连续的数组的下标。此处的解决办法就是开辟额外的数组（alls[]）存放原来的数组下标(被离散化的数的下标)。
手动模拟如下：
- ```
对于一组数如 ：[1,3,2000,50000,-99,2000,3,30],首先排序去重后----->[-99,1,3,30,2000,50000]
从排序去重后数组可以得到关系：-99 --> 0, 1 --> 1 , 3 --> 2, 30 -->3 ..........
上面对应的0，1，2，3，......都是此数字映射后对应的相对下标
```
- 离散化基本步骤可分为：
  
  1、离散化一定是有序的去离散化（排序）
  
  2、alls[]中可能存在重复元素（所以去重）
  
  3、如何算出X（求映射的下标）离散化后的值 (二分查找)
  
  注意：对于上述第三条，可以理解为去找这个数映射后的数组下标。

代码模板：

vector<int> alls; //存储所有待离散化的值
sort(alls.begin(),alls.begin());//将所有值排序
alls.erase(unique(alls.begin(),alls.end()),end());//去掉重复元素

//二分求出X对应的离散化的值（数组下标）
int find(int x)//找到第一个（最小）大于等于x的位置
{
    int l=0,r=alls.size()-1;
    while(l<r)
    {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r+1;//这里加1映射到（1，2，3，4.......n）,不加1的话映射到(0,1,2,3.....n)
}

关于代码中的unique函数和erase函数：

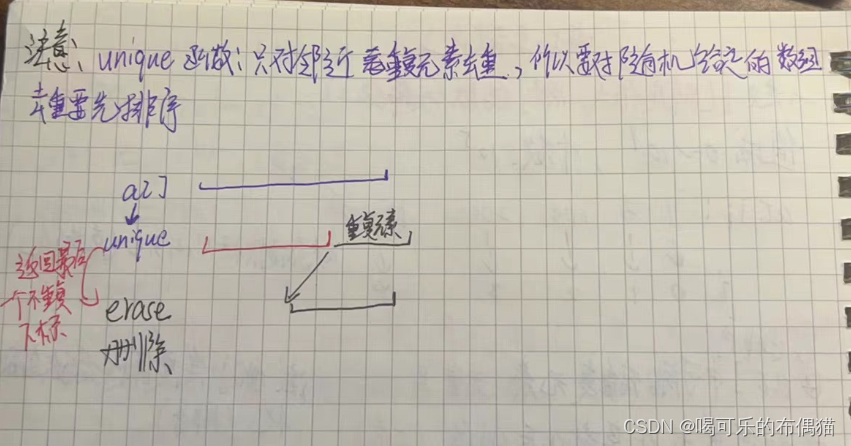如何自己实现unique函数：

例如：[1,1,2,2,2,3,4,5,5,5,6];
分为两步：
1、首先它是第一个元素
2、a[i] != a[i+1]

unique函数实现代码(双指针算法)：

vector<int> ::interator unique(vector<int> &a)
{
    for(int i=0;j=0;i<a.size();i++)
    {
        if(!i || a[i] != a[i-1])
        {
            a[j++] = a[i];
        }
    }
    //a[0]~a[j-1]中存的所有a[i]中不重复的数
    rerturn a.begin()+j;
}

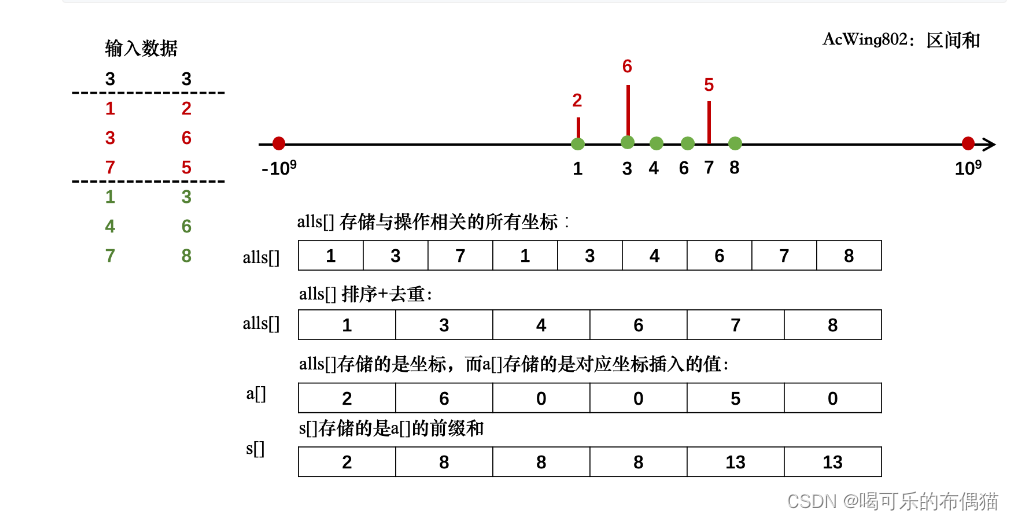
3、例题：802. 区间和 - AcWing题库

假定有一个无限长的数轴，数轴上每个坐标上的数都是 00。

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r。

输出格式

共 m行，每行输出一个询问中所求的区间内数字和。

数据范围

−10^9≤x≤10^9

1≤n,m≤10^5

−10^9≤l≤r≤10^9

−10000≤c≤10000

输入样例：

输出样例：

8
0
5

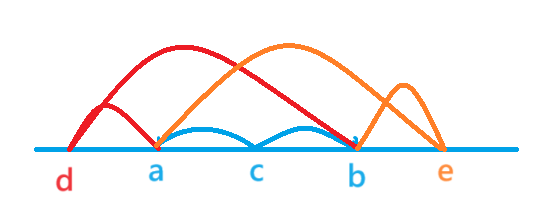
图解+分析(来源于大佬的题解分析)：

AC代码：

#include<iostream>
#include<algorithm>
#include<vector>
#include<utility>

using namespace std;

typedef pair<int, int> PII;

//这里开30W是因为n个x操作和2*m个坐标
const int N = 3e5+10;
int a[N],s[N];//前缀和数组
int n,m;
vector<int> alls;//离散化数组（对应下标值）
vector<PII> add,query;

int find(int x)//找到第一个最小的大于等于x的数
{
    int l = 0,r = alls.size()-1;
    while(l<r)
    {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    //如果+1映射从1，2，3........
    //否则从0，1，2，3、、、、、、、
    return r + 1;//返回映射
}

int main()
{
    cin >> n >> m;
    for(int i=0;i<n;i++)
    {
        int x,c;
        cin >> x >> c;
        //添加该位置加c的
        add.push_back({x,c});
        //把坐标放进离散化数组
        alls.push_back(x);
    }
    
    for(int i=0;i<m;i++)
    {
        int l,r;
        cin >> l >> r;
        //插入访问坐标
        query.push_back({l,r});
        //放入离散化数组里
        alls.push_back(l);
        alls.push_back(r);
    }
    
    //离散化板子
    sort(alls.begin(),alls.end());//排序
    //unique:返回去重后最后一个不重复元素的位置
    alls.erase(unique(alls.begin(),alls.end()),alls.end());//去重
    for(auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }
    
    //处理前缀和数组
    for(int i=1;i<=alls.size();i++) s[i] = s[i-1] + a[i];
    
    //处理询问
    for(auto item : query)
    {
        int l = find(item.first),r = find(item.second);
        cout << s[r] - s[l-1] << endl;
    }
    return 0;
}