在三维空间中,将曲线向曲面投影通常涉及复杂的几何计算。这个过程可以通过多种方法实现,但最常见的是使用数学和几何库,如OpenCASCADE,来处理这些计算。
在OpenCASCADE中,投影曲线到曲面通常涉及以下步骤:
定义曲线(Curve)和曲面(Surface)。
使用适当的算法或类(如BRepProj_Projection)来执行投影。
获取投影后的曲线。
下面是一个简化的例子,展示了如何使用OpenCASCADE的API来将一条曲线投影到一个曲面上:
#include <Geom_BezierCurve.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <TopoDS_Edge.hxx>
#include <BRep_Tool.hxx>
#include <BRepLib.hxx>
#include <TopoDS_Face.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#include <BRepBuilderAPI_Transform.hxx>
#include <gp_Ax3.hxx>
#include <gp_Cylinder.hxx>
#include <Geom_CylindricalSurface.hxx>
#include <BRepProj_Projection.hxx>
#include"Viewer.h"
int main(int argc, char* argv[])
{
//Non Rational B-Spline
gp_Pnt points1[8] = {
gp_Pnt(0.0,-100.0,0.0),
gp_Pnt(10.0,10.0,0.0),
gp_Pnt(30.0,-100.0,0.0),
gp_Pnt(100.0,0.0,0.0),
gp_Pnt(150.0,50.0,0.0),
gp_Pnt(200.0,0.0,0.0),
gp_Pnt(400.0,200.0,0.0),
gp_Pnt(450.0,0.0,0.0)
};
NCollection_Array1<gp_Pnt> points(points1[0], 1, 8);//Control points
Standard_Real realsWeight[8] = { 1.0,1.0,1.0,1.0,1.0,1.0,10.0,1.0 };
NCollection_Array1<Standard_Real> weight(realsWeight[0], 1, 8);//权系数,倒数第二个点的权系数是其他的10倍。
Geom_BezierCurve bezier(points); //Non-Rational
Handle(Geom_BezierCurve) bezier1 = &bezier;
TopoDS_Edge E = BRepBuilderAPI_MakeEdge(bezier1);
Handle(Geom_CylindricalSurface) aCylinder = new Geom_CylindricalSurface(gp::YOZ(), 200);
TopoDS_Shape Cylinder = BRepBuilderAPI_MakeFace(aCylinder->Cylinder(), 0, 2*M_PI, -200, 500);
BRepProj_Projection prj(E, Cylinder, gp_Dir(0.0, 0.0, 1.0));
//prj.Current();
Viewer vout(50, 50, 500, 500);
vout << E;
vout << Cylinder;
vout << prj.Current();
vout.StartMessageLoop();
return 0;
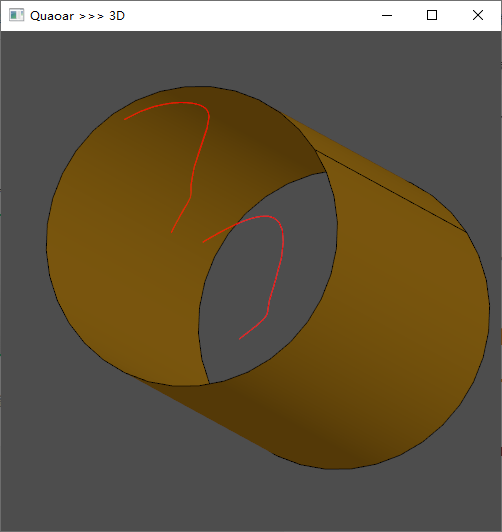
}



![[Flink03] Flink安装](https://img-blog.csdnimg.cn/img_convert/3bc059e0490c0289ab0fa93eb4313fe3.png)