👑作者主页：@进击的安度因
🏠学习社区：进击的安度因（个人社区）
📖专栏链接：有营养的算法笔记

一、前言

时隔多日，算法笔记终于又开始恢复更新了。今天 $anduin$ 为大家带来的是 高精度算法 。

高精度算法是解决大数运算的一把利器。虽然这个名字听起来挺高大上的，但是高精度算法的原理其实并不难，就和我们平时算计算题一样。所以学习起来还是十分愉快的。

高精度算法分为四大类，高精度加法，高精度减法，高精度乘法，高精度除法。它们各自有各自的优点。而今天，我们就来学习这四种算法。

二、高精度加法

1、思想及模板

高精度加法说白了就是两个大数之间相加，数字长度不超过 $10^6$ 。注意这里是长度，而不是数据大小哦！

但是这种数字如果放到变量中肯定是存不下的，所以我们一般用数组来存储，在 C++ 中一般用 vector 容器。

如果存入数组中，就需要考虑存储顺序，究竟应该正着存还是倒着存。

实际上，我们这边 倒着存 是很合适的，因为对于数组来说，给一个数的后面一个数加 $1$ 很简单，但是在一个数的前面加上 $1$ 就很麻烦。

就比如这张图：

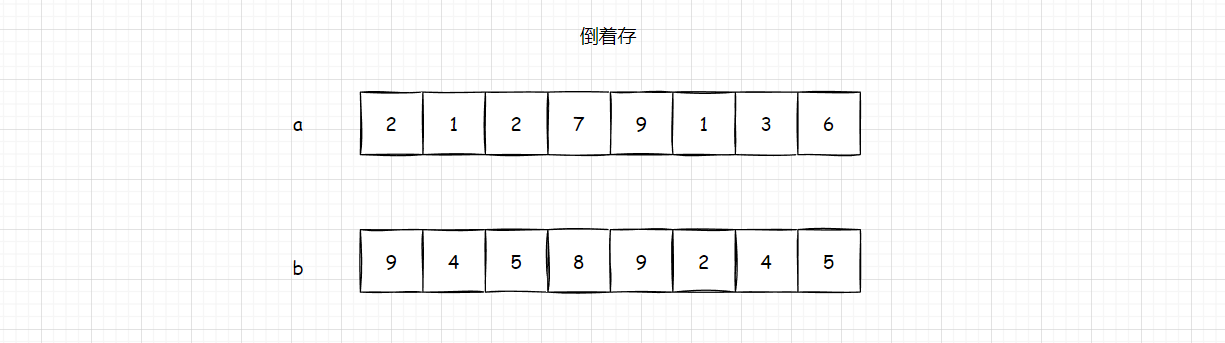
如果我们 倒着存 那么 a[0] + b[0] = 11 ，是需要进位的。如果倒着存就可以 很快的进行进位 ，直接在下标 $1$ 处进行自增即可；但是如果正着存，那么进位就需要到 $-1$ 下标了，这样就不麻烦，我们算法就是为了更快解决问题，所以自然选择最合适的方式：倒着存 。

而高精度加法运算其实就像我们小学列 竖式 一样：

从最低位开始计算，如果两个数相加超过 $10$ ，就需要进位。竖式我就不带着大家列了，相信以小伙伴的脑袋瓜很容易想明白。

我这边就讲一下思想：

假如数组 $a$ 和 $b$ 分别用来存数据，$c$ 用来存储答案。

通过循环同时遍历 $a$ 、$b$ 数组，在遍历的同时，使用 $t$ 来判断是否进位。将 a[i] + b[i] 的数据累加到 $t$ 中。

数据相加有两种结果：

• 如果 a[i] + b[i] < 10 ，直接将 t 放入 $c$ ，让 t /= 10 ，以便下一次计算。
• 如果 a[i] + b[i] = 10 ，将 t % 10 = 0 放入 $c$ ，让 t /= 10 。
• 如果 a[i] + b[i] > 10 ，将 t % 10 放入 $c$ 数组，将 t /= 10 作为 进位 ，下一次 $t$ 初始就是 $1$ 。

就拿这张图理解：

这里就是对最后一位进行运算时，所做的进位操作。

而 $t\%10$ 最终的结果肯定在 $0\sim 9$ 之间，如果 $t<10$ 小，那么 $\%10$ 不会对运算结果产生影响；对于 $t>10$的情况，则会将结果控制到 $0\sim 9$ 之间。

这种做法就像是计算机在模拟我们日常的操作，所以高精度加法在力扣上有一题被归为 模拟算法 的范畴：415. 字符串相加 。就比如这道题目，就是经典的高精度加法。

模板 ：

vector<int> Add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i++) {
        if (i < A.size()) {
            t += A[i];
        }
        if (i < B.size()) {
            t += B[i];
        }
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) {
        C.push_back(1);
    }
    return C;
}

简单讲一下模板在干什么：

$a$ 和 $b$ 是倒着存的，并同步遍历，由于数据大小不确定，所以只要 $a$ 和 $b$ 有一个符合条件，则就可以被 $t$ 累加。

每次将 $t$ 尾插到结果数组 $c$ 中，然后将 $t/10$ ，以便下次运算，如果有进位，那么下次 $t$ 的初值就为 $1$ 。

最后循环结束后，再判断一下是否还有进位没进，如果有进位，则将 $1$ 尾插到 $c$ 中。

2、代码实现

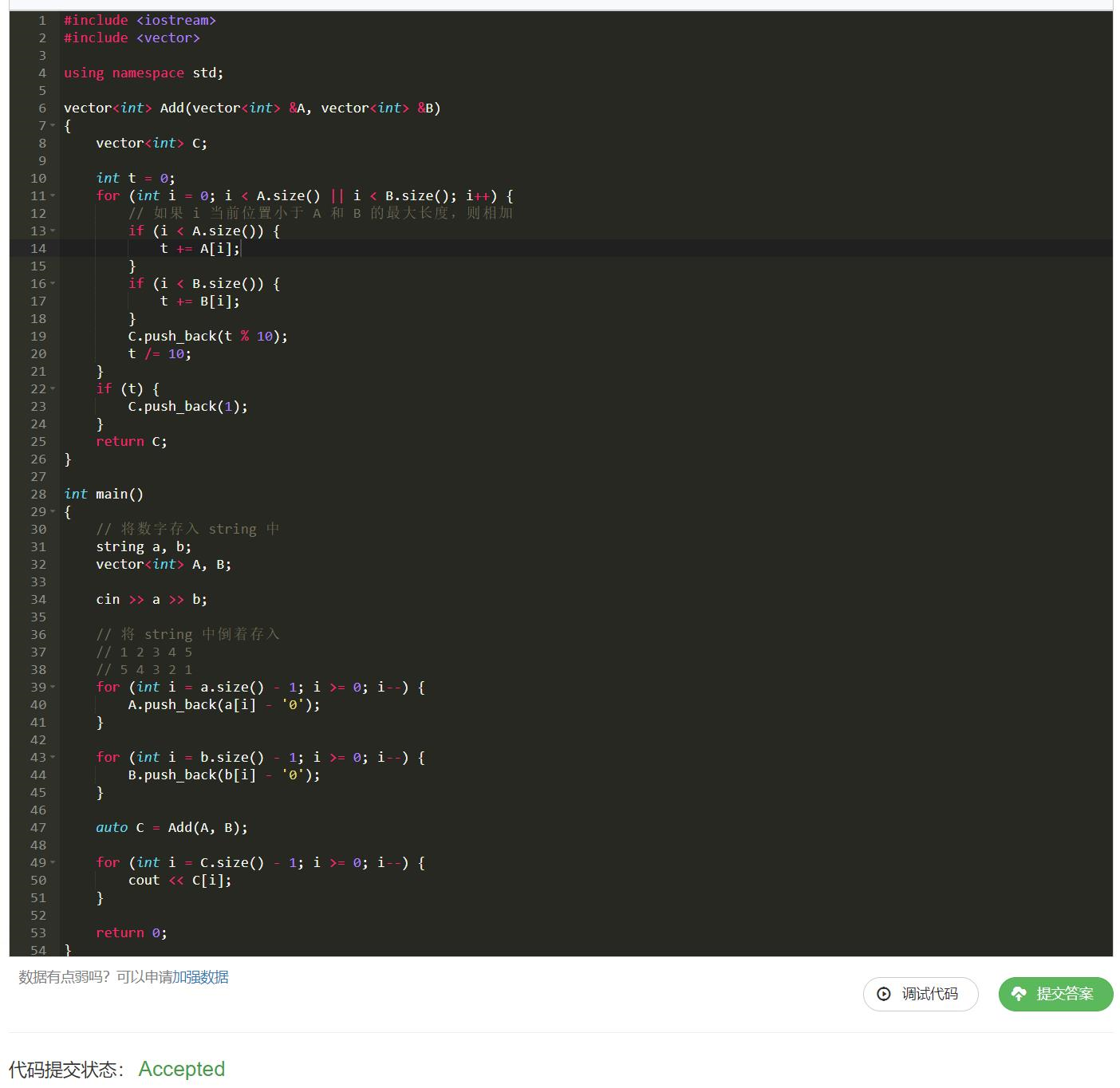
链接：791. 高精度加法

描述：

给定两个正整数（不含前导 $0$），计算它们的和。

输入格式：

共两行，每行包含一个整数。

输出格式：

共一行，包含所求的和。

数据范围：

$1\le$ 整数长度 $\le 100000$

输入样例：

12
23

输出样例：

35

思路 ：

思路我们基本已经讲完了，在经过模板中的处理后，将数据倒着打印出来即可。

三、高精度减法

1、思路及模板

高精度减法是对大整数的减法，数据长度不超过 $10^6$ 。

我们讲解的 高精度减法是基于对正整数的算法 ，如果计算的是负数，那么需要微调。

高精度减法使用的存储方式为 倒序存储 。还是和我们的竖式计算十分相似。

假设我们现在还是两个数组：$a,b$ ，当 $a[i]-b[i]<0$ 时，则需要 借位 ；如果 $a[i]-b[i]>=0$ ，则无需处理。

就比如这幅图就是 $a[i]-b[i]<0$ 的一个经典样例：

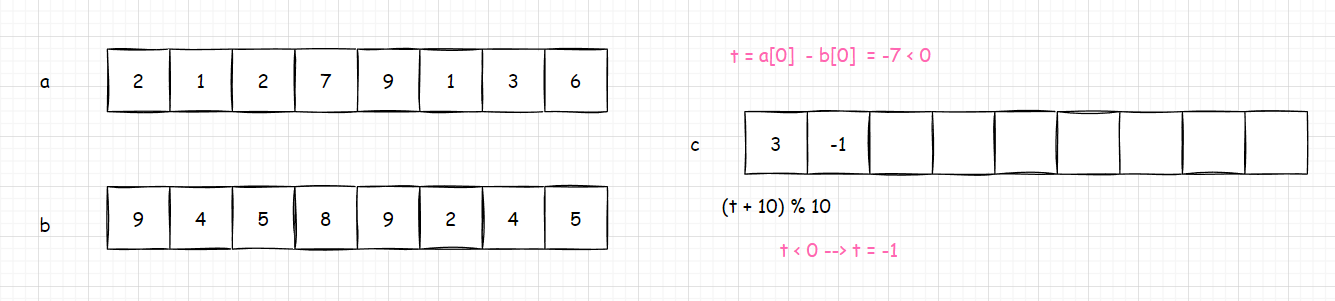
如果 $a[i]-b[i]<0$ ，则说明需要借位，就是 $+10$ ，为了防止 $+10$ 后超过 $10$ 而放不进数组，所以需要 $\%10$ 。然后判断 $t$本身是否小于 $0$ ，将借位更新一下：$t=-1$ ，方便下一次计算。

如果 $a[i]-b[i]\ge 0$ ，上面的方式也能完全适应，因为对于 $0\sim 9$ 的正数来说先 $+10$ 再 $\%10$ 是不变的，所以方法完全适配。在这种情况下 $t\ge 0$ ，所以无需进位 $t=0$ 。

但是在进行高精度减法之前，我们需要知道两个数的大小：

• 若 $a<b$ ，则 $a-b$ 结果为负数
• 若 $a\ge b$ ，则 $a-b$ 结果为整数或 $0$

所以我们需要预处理比较两个数的大小，如果 $a<b$ 的话，就需要交换它们的值，因为它俩原结果就相当于 $-(b-a)$ 。

再来看看模板：

// 比较 a 和 b 的大小
bool cmp(vector<int> &A, vector<int> &B)
{
    // 如果 A 的位数小于或等于 B 的位数
    if (A.size() != B.size()) {
        return A.size() > B.size();
    }
    // A 的位数大于 B 的位数
    for (int i = A.size() - 1; i >= 0; i--) {
        if (A[i] != B[i]) {
            return A[i] > B[i];
        }
    }
    // 此时 A == B
    return true;
}

vector<int> Sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t += A[i];
        if (i < B.size()) {
            t -= B[i];
        }
        // 相减结果可能为负数 % 10 可以得到 0~9 的位数
        // 此时是需要借位的
        C.push_back((t + 10) % 10);
        // 如果 t < 0 说明要借位
        if (t < 0) {
            t = -1;
        } else {
            t = 0;
        }
    }
    while (C.size() > 1 && C.back() == 0) {
        C.pop_back();
    }
    return C;
}

这段模板里的大部分我们都讲过了，下面讲一下这块是什么意思：

while (C.size() > 1 && C.back() == 0) {
        C.pop_back();
}

由于我们的数据时是倒着存放的，而两个数相减结果为 $0$ ，就会在该位填上 $0$ 。

比如 $666\sim 665$ 在经过上方的高精度运算后，$c$ 中结果为 $100$ ，所以这种情况就需要去前导0 。

上面的操作就是检查长度是否至少为 $1$ ，且 $c$ 尾部是否为 $0$ 。

2、代码实现

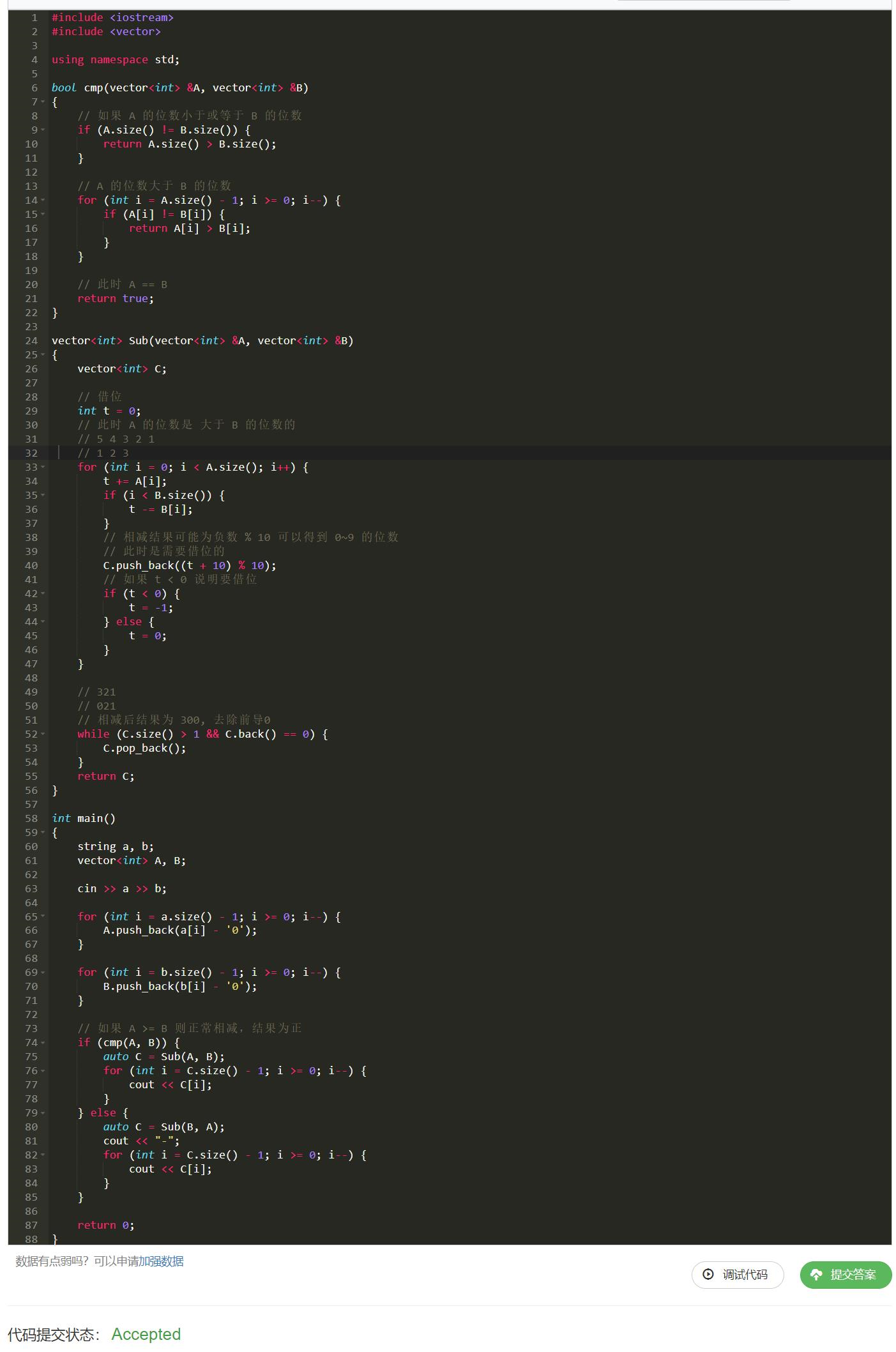
链接 ：792. 高精度减法

给定两个正整数（不含前导 $0$ ），计算它们的差，计算结果可能为负数。

输入格式：

共两行，每行包含一个整数。

输出格式：

共一行，包含所求的差。

数据范围：

$1\le 整数长度\le 10_5$

输入样例：

32
11

输出样例：

21

思路我们都讲过了，接下来就直接上代码，注意点都在注释里：

四、高精度乘法

1、思路及模板

我们这里讲的高精度乘法为大整数 $\times$ 小整数，大整数长度不超过 $10^6$，小整数数据范围不超过$10^9$。

高精度乘法，就不只是单单的数学计算了，这里有些不同。

首先大数 $a$ 倒序存储到 vector 中，这样也是为了方便进位，首先设定进位 $t$ 。

再看一个例子，了解一下进位规则：

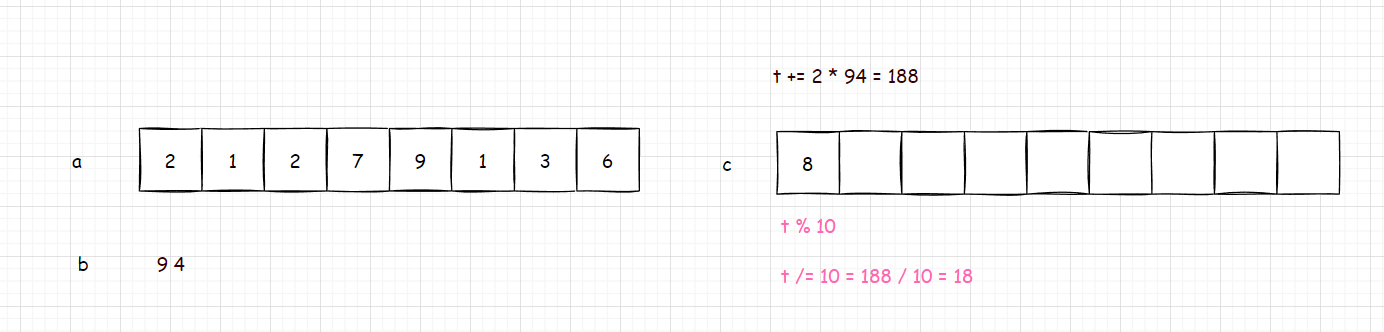
就比如这个例子，大数 $a$ 的单独位数直接和 $b$ 相乘，将结果累加到 $t$ 中，将乘得的结果 $\%10$ 存放到 $c$ 数组中，然后 $t/=10$ ，将进位去掉一位 。其实这里的进位也很好理解，无非就是要让 $t$ 到下一位，而下一位是当前位次 $\times 10$ ，所以 $t$ 要前进一位就要 $/10$ 。

这就是高精度乘法的运算规则，也不需要分类讨论啥的，就记住这个规律就好。虽然运算方法和我们从前计算方式有些不同，但是最终计算结果是相同的。

由于这个过程不太好模拟，所以不懂的小伙伴们可以下去自己模拟一下，操作很简单，但是不好表示。

模板 ：

vector<int> Mul(vector<int> &A, int b) 
{
    vector<int> C;
    
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    while (t) {
        C.push_back(t % 10);
        t /= 10;
    }
    
    // 去除前导 0 
    while (C.size() > 1 && C.back() == 0) {
        C.pop_back();
    }
    return C;
}

我们再来讲讲模板里面的部分内容：

第一部分：

while (t) {
    C.push_back(t % 10);
    t /= 10;
}

这一部分就是在处理进位，因为运算结束之后，很可能还有进位没有处理。所以循环结束需要额外处理一下。

第二部分：

// 去除前导 0 
while (C.size() > 1 && C.back() == 0) {
    C.pop_back();
}

乘法也是会出现前导 $0$ 的，比如任何一个数和 $0$ 相乘结果都会是 $0$，所以这里也需要去一下前导 $0$ 。

2、代码实现

链接：793. 高精度乘法

描述：

给定两个非负整数（不含前导 $0$ ） $A$ 和 $B$ ，请你计算 $A\times B$ 的值。

输入格式：

共两行，第一行包含整数 $A$ ，第二行包含整数 $B$ 。

输出格式：

共一行，包含 $A\times B$ 的值。

数据范围：

$1\le A的长度\le 100000$
$0\le B\le 10000$

输入样例：

2
3

输出样例：

6

由于上面我们基本上已经把代码讲过了，所以直接上代码，高精度乘法其实思路十分简单：

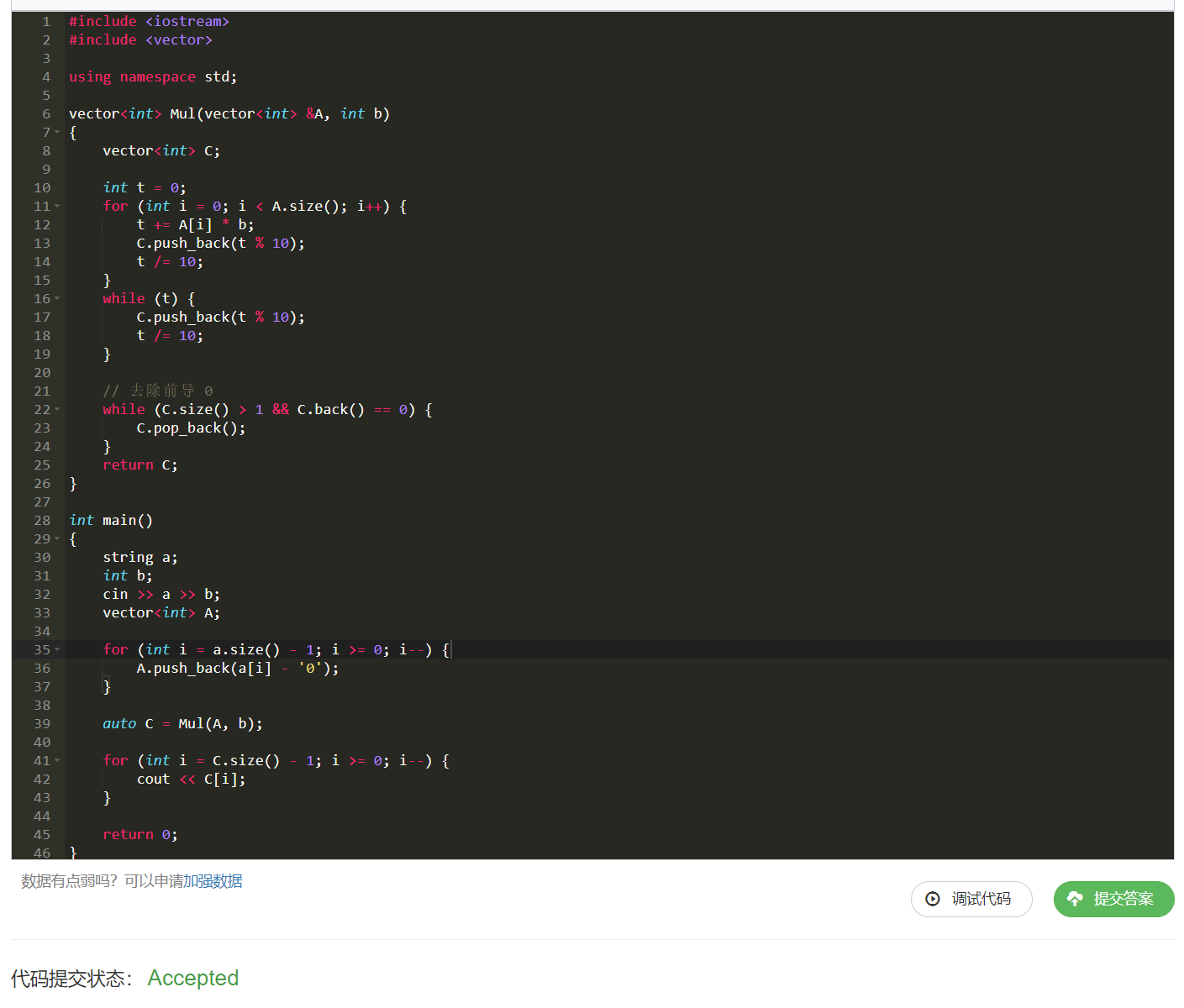
五、高精度除法

1、思路及模板

我们这里讲的高精度除法为大整数 $/$ 小整数，大整数长度不超过 $10^6$，小整数数据范围不超过$10^9$。

我们人在做除法时，会先看第一位，如果第一位大于除数，则在结果相应位置写下除以除数之后的数据，否则看下一位，这样以此类推。所以人算除法第一位都是有效数据位。

但是对于计算机不是这样，计算机则会默认从第一位算起，举个例子，比如 $1234/11$ ：如果以人的角度，第一位肯定为 $1$ ，但是计算机会从第一位开始看，第一位为 $0$ 。

而 除法可能产生余数 ，所以还需要一个变量来记录余数。

有了这个概念，我们先看模板：

我们的模板是倒着存数据的，但是高精度除法是可以正着存的，因为除法需要从第一位开始除，所以正着存完全没有问题，但是之后可能会有高精度的混合运算，所以我们这边保持标准，也是倒着存。

vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    
    r = 0;
    
    for (int i = A.size() - 1; i >= 0; i--) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    
    reverse(C.begin(), C.end());
    
    while (C.size() > 1 && C.back() == 0) {
        C.pop_back();
    }
    
    return C;
}

看完模板之后，我们对立面的一些代码进行讲解 ：

第一块：

for (int i = A.size() - 1; i >= 0; i--) {
    r = r * 10 + A[i];
    C.push_back(r / b);
    r %= b;
}

首先看着一步，高精度除法比另外三个算法难的原因就是出在这一步上，因为运算规则可能不太好理解。

我们知道，如果要做除法运算，那么后面就需要一定的 补位 ，r * 10 + A[i] 就是在补位，因为下一次的需要被除的数据，就是第一次相除后的余数 $\times 10$ ，然后加上当前元素 A[i] 。

而除之后的结果就是 $r/b$ ，每次除完都有相应的余数，所以 r %= b 。下面我们就用一张图演示一下：

通过这张图，我们就可以完美的解释代码究竟在干什么，实际上这就是一个计算的过程，过程设计补位，相除，得余数等操作…

而最后，在进行完所有的操作之后 $r$ 其实就是最终的余数。

第二块：

reverse(C.begin(), C.end());
    
while (C.size() > 1 && C.back() == 0) {
    C.pop_back();
}

这两步就是在去前导 $0$ ，上面的图中我们也可以发现，高精度除法也是有前导 $0$ 的，但是对于顺序表来说，前导 $0$不太好去，所以就逆置一下再去前导 $0$ 。

最后倒着输出 $c$ 即可。

2、代码实现

链接：794. 高精度除法

描述：

给定两个非负整数（不含前导 $0$ ） $A，B$ 请你计算 $A/B$ 的商和余数。

输入格式：

共两行，第一行包含整数 $A$ ，第二行包含整数 $B$ 。

输出格式：

共两行，第一行输出所求的商，第二行输出所求余数。

数据范围：

$1\le A的长度\le 100000$
$1\le B\le 10000$
$B$ 一定不为 $0$

输入样例：

7
2

输出样例：

3
1

思路我们说过了，接下来我把 倒着存 和 正着存 的两个版本都贴上来。

倒着存 ：

正着存：

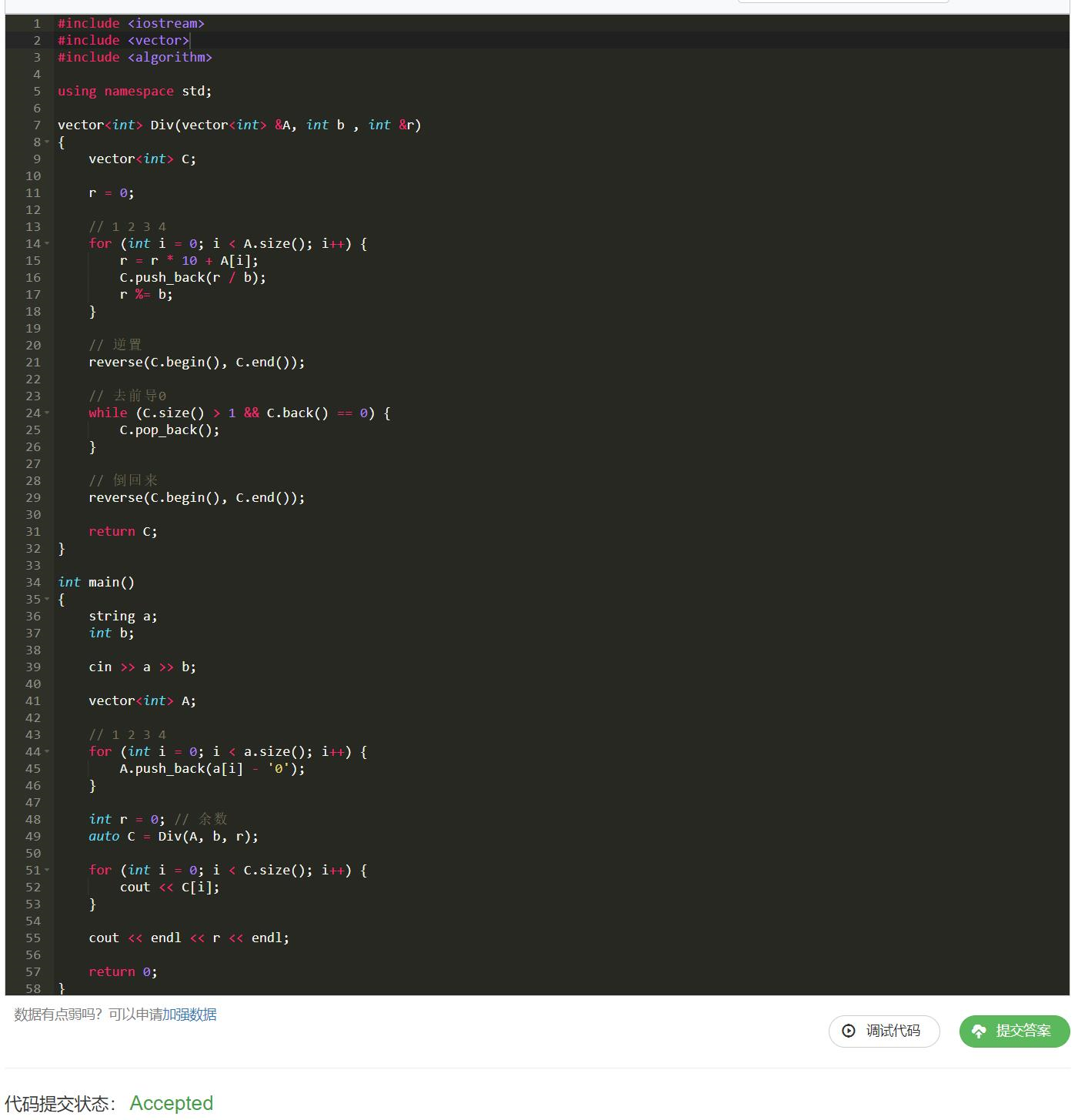
六、结语

到这里，本篇文章就到此结束了，实际上高精度算法这一块还是很容易理解的，因为我们可以模拟他们计算的过程，所以对于一些细节不太了解的小伙伴们可以下去模拟一下。

一般来说，只要背过模板做这类问题就信手拈来了。所以不必担心嘿嘿。

当然，小伙伴们最好也找两道高精度问题练练手。我们不仅要看懂，还要会写。

如果觉得 $anduin$ 写的还不错的话，可以点赞 + 评论 + 收藏支持一下，我们下期见~