阅读《scala编程》时，我们知道了类的类型参数是可以型变（variance）的。型变包含以下三种：

• 协变（convariant）：如果S是T的子类型，则C1[S]也是C1[T]的子类型，则称C1在类型参数T上是协变的。通过定义时再T前面加上+实现。class C1[+T]。P393
• 不变（nonvariant）：不同类型的队列之间永远不存在子类型关系。泛型默认是不变的。 P394
• 逆变（contravariance）：如果S是T的子类型，则C1[T]是C1[S]的子类型。通过定义时再T前面加上-实现。class C1[-T]。

类或特质定义中能出现类型参数的所有位置都会被归类成不同的“点”,这些点可分为

• 协变点(positive)
• 逆变点(negetive)
• 不变点(neutral)。

类型参数在使用上遵守以下规则：

• 用+注解的类型参数只能用在协变点。
• 用-注解的类型参数只能用在逆变点。
• 不用注解的类型参数，可以用再任意点。（也是唯一能用在不变点的类型参数）

令人困扰的是，如何确定，各个位置是什么类型的点呢？书中如下结论到底是怎么来的？

abstract class Cat[-T, +U] {
    def meow[W](volume: T, listener: Cat[U, T]): Cat[Cat[U, T], U]
}
// 书中给的各类型参数的结论如下：+表示协变点，-表示逆变点
abstract class Cat[-T, +U] {
    def meow[W-](volume: T-, listener: Cat[U+, T-]-): Cat[Cat[U+, T-]-, U+]+
}

确定点的类型有如下基本规则和例外情况，按照基本规则和例外情况就可以分析出所有点的类型了。

基本规则：

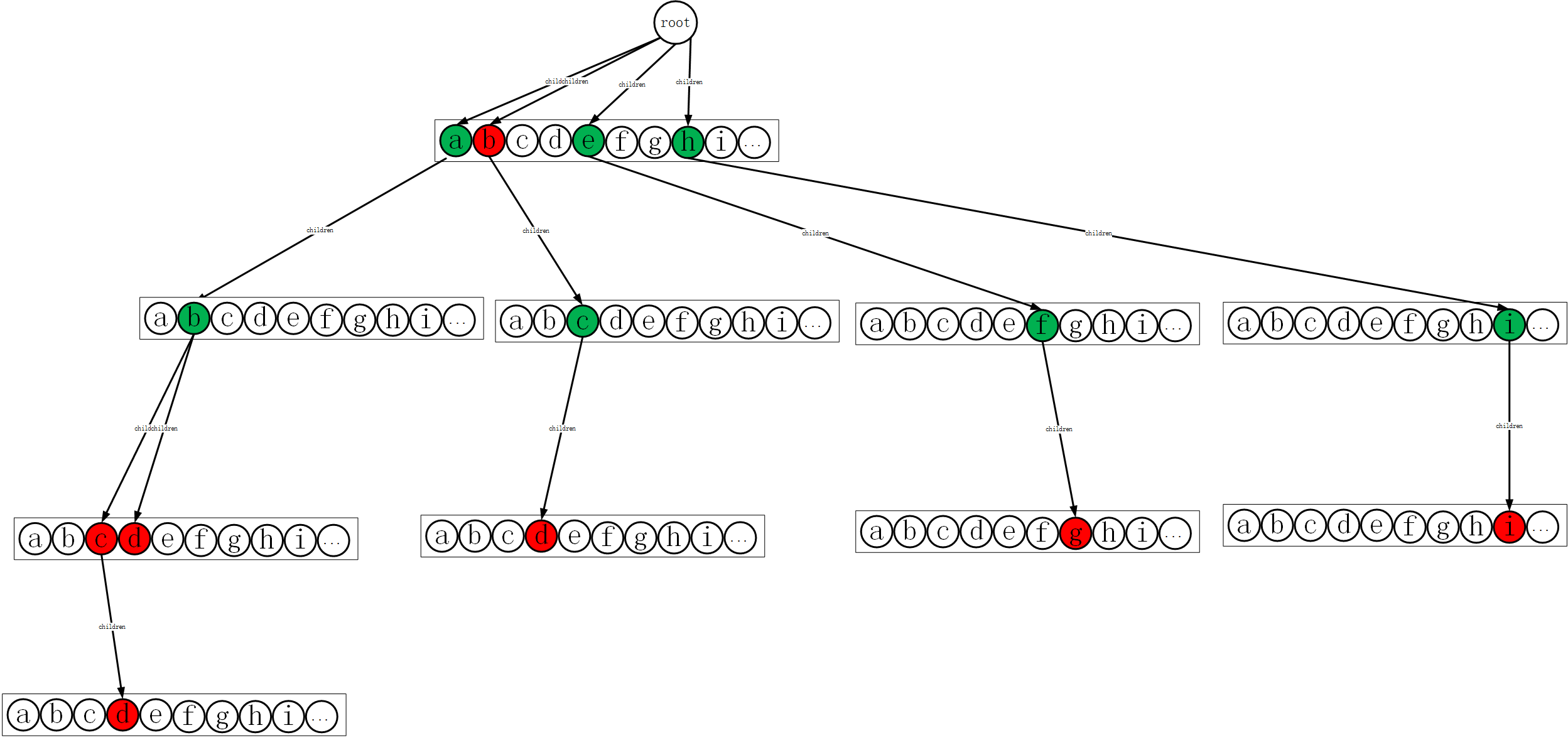
1. 从类（或特质）的定义处开始，所有类型参数按照类的嵌套定义生成一颗树。如下图所示。
2. 树顶部是协变点(positive)
3. 更深嵌套的层次的点默认跟它上一层的类型相同

如果有更多其他成员在meow一层定义（如def、 val、 var、 type等），则meow一层还有更多分支。

例外情况：

1. 方法入参的类型参数的位置被归纳为“翻转”类，具有以下性质：、
   • 逆变点翻转为协变点
   • 协变点翻转为逆变点
   • 不变点翻转后仍为不变点
2. 方法本身的类型参数的位置也属于“翻转”类。如def f[T]中T的位置。
3. 类型的类型参数的位置（原文是 type argument position of a type），如a: C[T]中的T，根据C在定义时,T的声明的型变决定，具体的：
   • +T 则类型保持不变
   • -T 则类型变为“翻转”
   • T 则类型变为“不变点”(neutral)

解释书中的样例

abstract class Cat[-T, +U] {
    def meow[W](volume: T, listener: Cat[U, T]): Cat[Cat[U, T], U]
}
// 书中给的各类型参数的结论如下：+表示协变点，-表示逆变点
abstract class Cat[-T, +U] {
    def meow[W-](volume: T-, listener: Cat[U+, T-]-): Cat[Cat[U+, T-]-, U+]+
}

具体解释，以下A-J表示位置：

// 顶点是+的，所以根据基本规则3，则应该有底层的A B C D四个位置都是+的
abstract class Cat[-T, +U] {
    def meow[A](volume: B, listener: C): D
}
// 根据例外情况2，则A翻转，由+变成-的
abstract class Cat[-T, +U] {
    def meow[A-](volume: B, listener: C): D
}

// 根据例外情况1,B，C都翻转成-的，D没有例外，仍是+
abstract class Cat[-T, +U] {
    def meow[A-](volume: B-, listener: C-): D+
}
//C位置继续往下嵌套为Cat[U, T]，所以Cat[E, F]的E，F两个位置根据基本规则3,继承C处类型-，
// 然后根据例外情况3，E处定义时为-T，需翻转为+；F处定义时为+U,保持不变为-，则C位置最终为Cat[E+, F-]-
abstract class Cat[-T, +U] {
    def meow[A-](volume: B-, listener: Cat[E+, F-]-): D+
}
// D位置也类似C位置的经过两步分析，第1步得到 Cat[G-, H+]+，第2步得到Cat[Cat[I+, J-]-, H+]+所以最终为：
abstract class Cat[-T, +U] {
     def meow[A-](volume: B-, listener: Cat[E+, F-]-): Cat[Cat[I+, J-]-, H+]+
}

把位置处带入类型参数，即为书本上的结果：
abstract class Cat[-T, +U] {
    def meow[W-](volume: T-, listener: Cat[U+, T-]-): Cat[Cat[U+, T-]-, U+]+
}

参考

• 参考1
• 参考2
• 参考3