题目

Trie（发音类似 “try”）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。
请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例

输入[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”][[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]输出[null, null, true, false, true, null, true]
解释Trie trie = new Trie();trie.insert(“apple”);trie.search(“apple”); // 返回 Truetrie.search(“app”); // 返回 Falsetrie.startsWith(“app”); // 返回 Truetrie.insert(“app”);trie.search(“app”); // 返回 True

题解：

字典树（前缀树）的介绍

字典树是什么？

字典树是一种树型结构，它是hash树的一种变种。其有大量的应用，比如搜索引擎中用于文本词频统计。其优点是利用字符串的公共前缀来减少查询时间，减少字符串的比较次数。

直接用列子来说明字典树是什么。现假设有有b，abc，abd，bcd，abcd，efg，hii 这6个单词。那么我们看看基于这几个单词如何来构建字典树。这里假设所有字符均是小写字母
对于单词b，构建结果如下图。

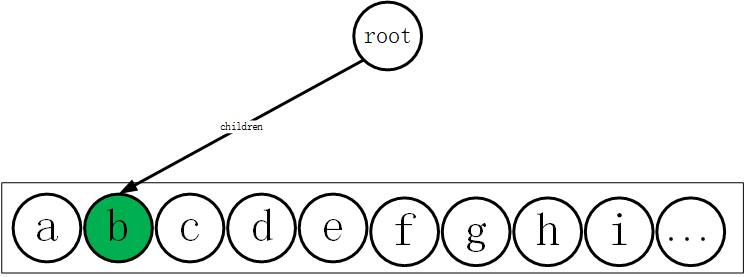
同时由于b也是该单词的重点因此需要对其进行标记，用红色标记为终止节点。

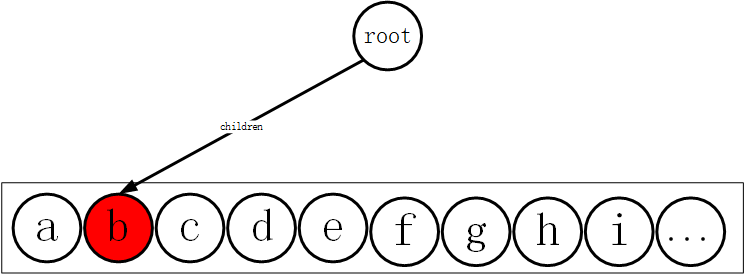
接下来看abc单词。

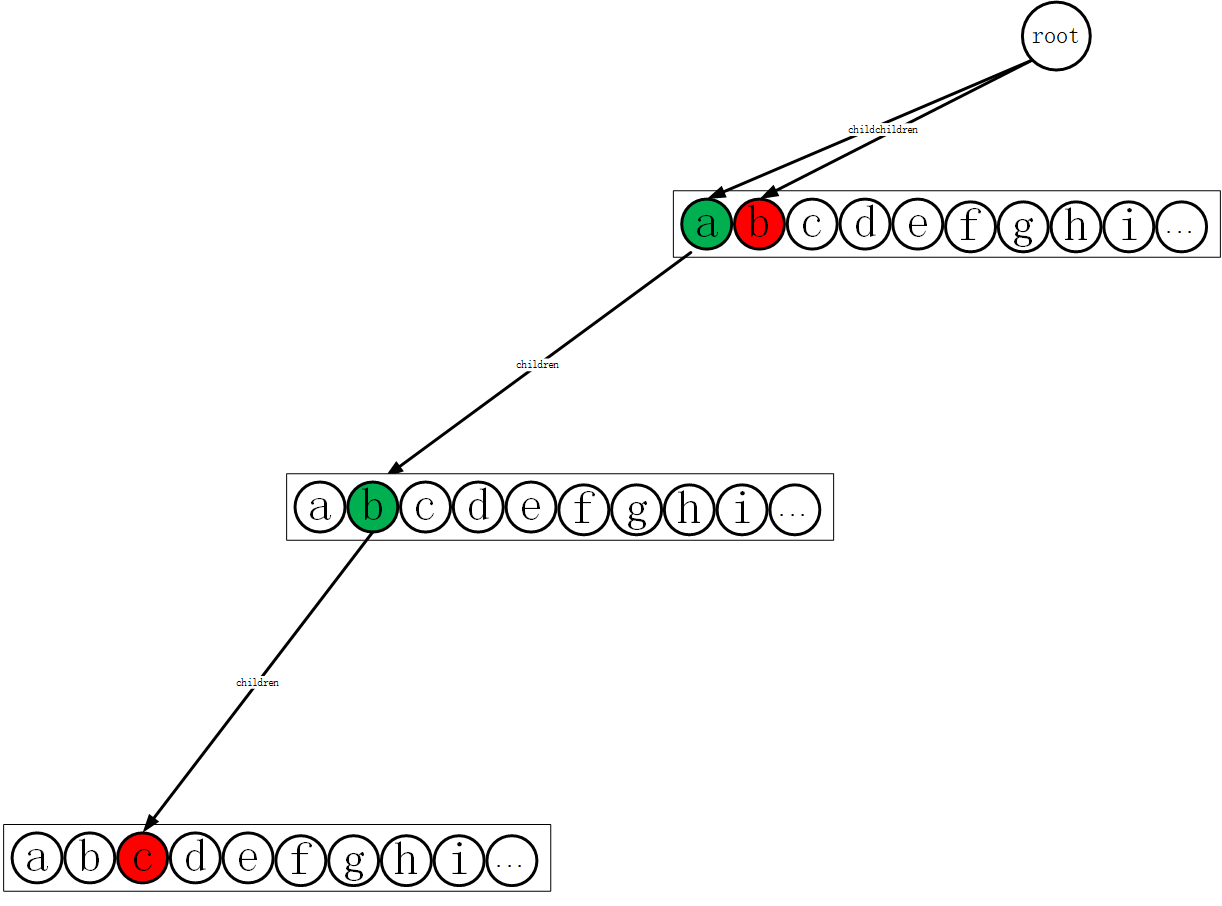
接下来把bcd单词插入到字典树中如下图所示。

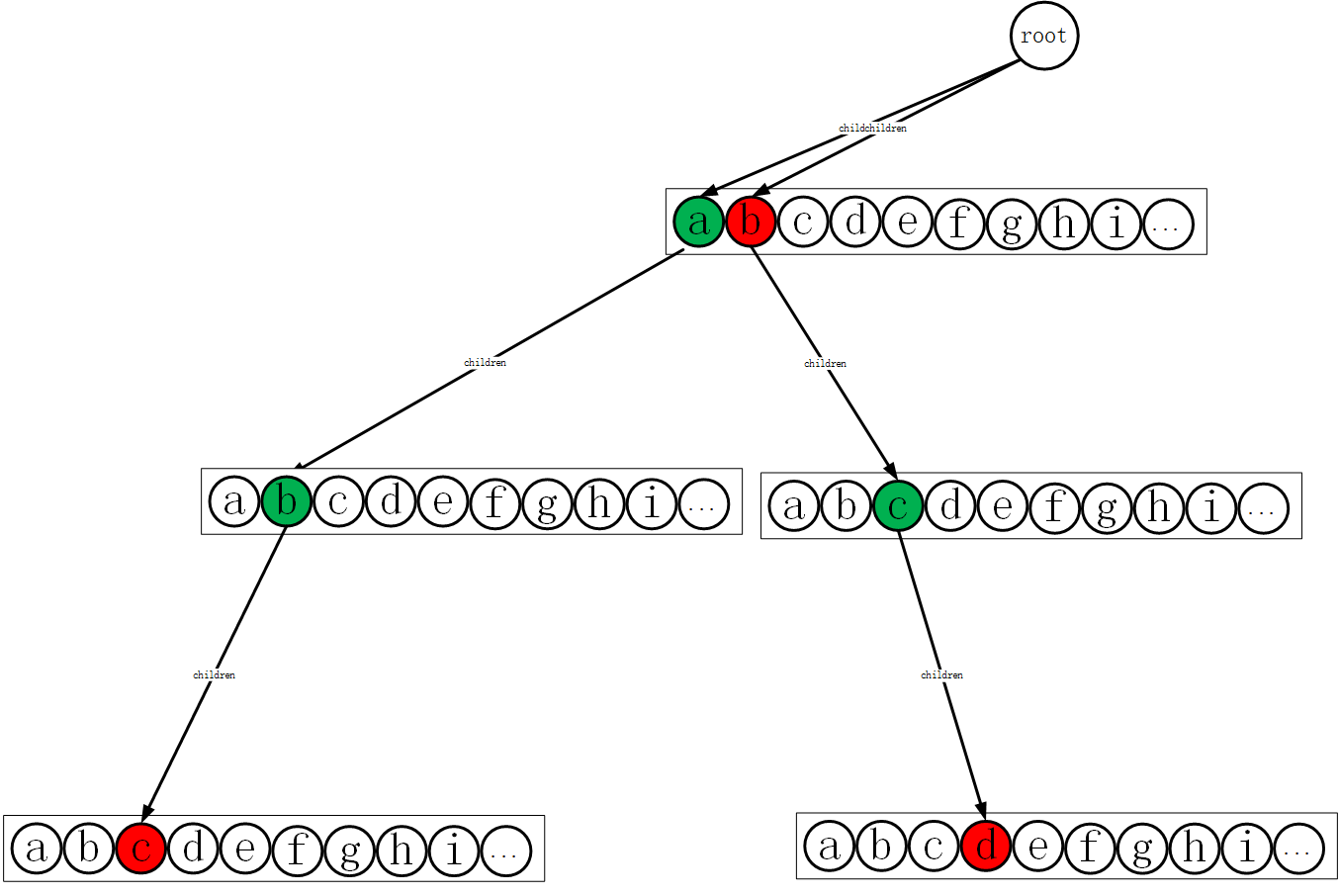
把所有的单词插入到字典树之后如下图所示。

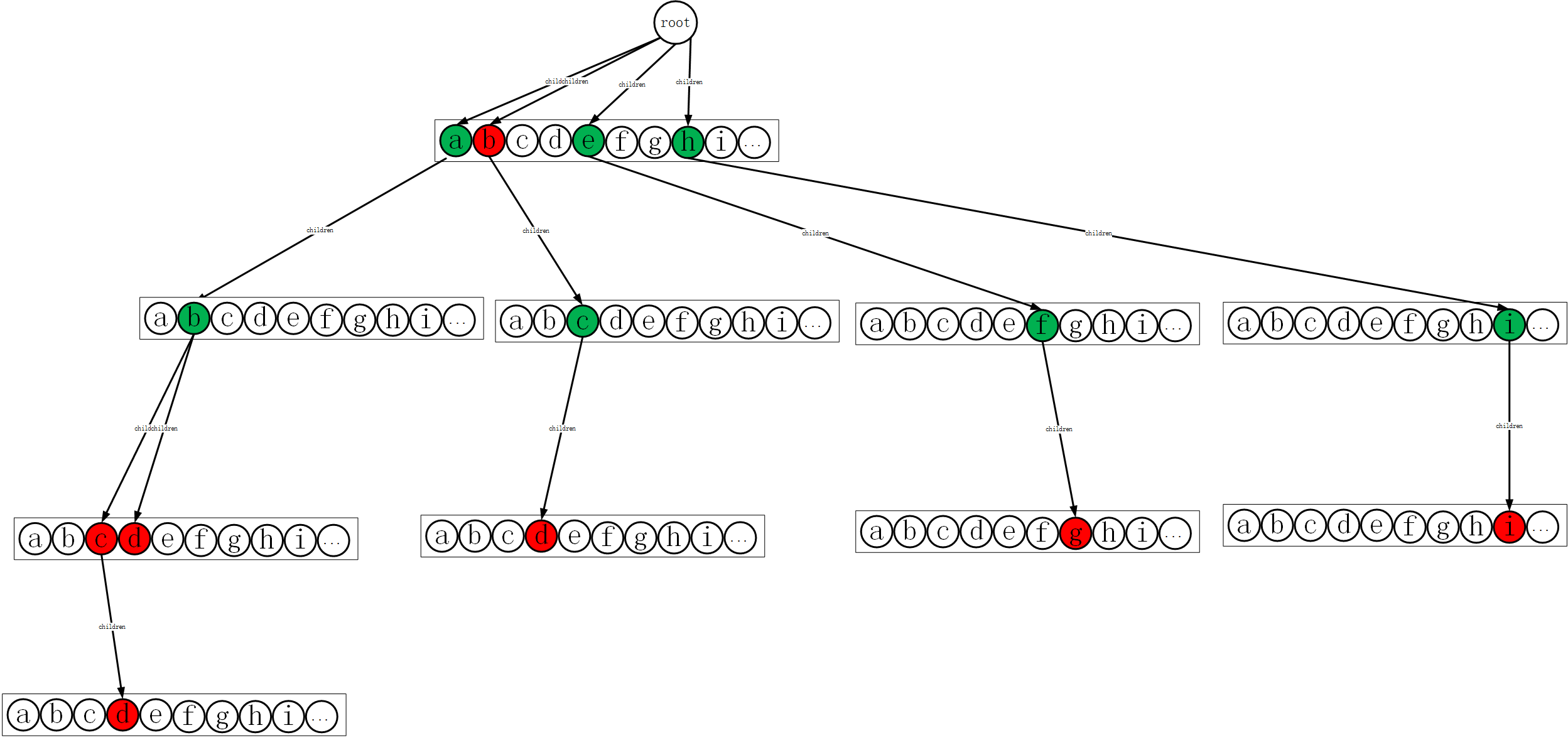
因此字典数据的构建就完成了。到这里其实就可以根据题目要求来写代码了。

题目分析

可见字典树的节点的数据结构有两个关键，一个是指向children的指针列表，一个是表示是否是字符串终点的flag
主要有三个函数：

插入字符串
主要有两种情况：1如果当前字符在子节点中存在则继续向下遍历，2 如果不存在则创建一个新子节点。这里遍历完所有字符最后别忘了把最后的节点标记为字符串终点。
搜索字符串
这个其实也类似也分两种情况，如果字符串没找到直接 false，如果找到最后一个不是字符串终点也是false，否则为true。
搜索前缀这个跟搜索字符串类似但是不用考虑是否是字符串终点了
代码如下：

class Trie:

    def __init__(self):
        #子节点
        self.children=[None]*26
        self.isEnde=False
        


    def insert(self, word: str) -> None:
        node=self
        for ch in word:
            num=ord(ch)-ord("a")
            #如果该字符不在其子节点中则创建一个
            if not node.children[num]:
                node.children[num]=Trie()
            #node跳到下一节点
            node = node.children[num]
        node.isEnde=True


    def search(self, word: str) -> bool:
        node =self
        for ch in word:
            num=ord(ch)-ord("a")
            if node.children[num]:

                node=node.children[num]
            else:
                return False
        if node.isEnde:
            return True
        return False
        


    def startsWith(self, prefix: str) -> bool:
        node = self
        for ch in prefix:
            num=ord(ch)-ord("a")
            if node.children[num]:
                node=node.children[num]
            else:
                return False
        return True