本文为Python算法题集之一的代码示例

题94：

1. 示例说明

• 给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

  示例 1：

  

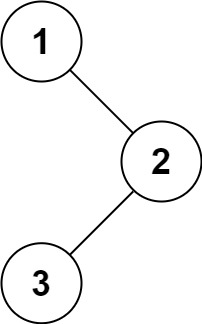
  输入：root = [1,null,2,3]
  输出：[1,3,2]
  

  示例 2：

  输入：root = []
  输出：[]
  

  示例 3：

  输入：root = [1]
  输出：[1]
  

  提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

  进阶: 递归算法很简单，你可以通过迭代算法完成吗？

---

2. 题目解析

- 题意分解

1. 本题为二叉树的中序遍历
2. 基本的设计思路是采用递归，首先遍历左子树，然后访问根结点，最后遍历右子树

- 优化思路

1. 通常优化：减少循环层次

2. 通常优化：增加分支，减少计算集

3. 通常优化：采用内置算法来提升计算速度

4. 分析题目特点，分析最优解

   1. 可以考虑采用迭代法改写递归，提高性能

---

- 测量工具

• 本地化测试说明：LeetCode网站测试运行时数据波动很大，因此需要本地化测试解决这个问题
• CheckFuncPerf（本地化函数用时和内存占用测试模块）已上传到CSDN，地址：Python算法题集_检测函数用时和内存占用的模块
• 本题本地化超时测试用例自己生成，详见【最优算法章节】

---

3. 代码展开

1) 标准求解【直接递归】

直接写明中序遍历次序的递归，左子树、根、右子树写在一行上

马马虎虎，超过77%

import CheckFuncPerf as cfp

class Solution:
 def inorderTraversal_base(self, root):
     if not root:
         return []
     return self.inorderTraversal_base(root.left) + [root.val] + self.inorderTraversal_base(root.right)

aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.inorderTraversal_base, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result'][0]))

# 运行结果
函数 inorderTraversal_base 的运行时间为 654.17 ms；内存使用量为 8284.00 KB 执行结果 = 81

2) 改进版一【函数递归】

编写递归子函数，减少递归时缓存的资源

性能良好，超过85%

import CheckFuncPerf as cfp

class Solution:
 def inorderTraversal_ext1(self, root):
     def inOrder(root, result):
         if root == None:
             return
         inOrder(root.left, result)
         result.append(root.val)
         inOrder(root.right, result)
     result = []
     inOrder(root, result)
     return result

aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.inorderTraversal_ext1, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result'][0]))

# 运行结果
函数 inorderTraversal_ext1 的运行时间为 489.10 ms；内存使用量为 9556.00 KB 执行结果 = 81

3) 改进版二【迭代遍历】

采用堆栈来模拟递归，减少资源消耗

极速狂飙，超过98%

import CheckFuncPerf as cfp

class Solution:
 def inorderTraversal_ext2(self, root):
     if not root:
         return []
     list_stack = []
     result = []
     while root or list_stack:
         if root:
             list_stack.append(root)
             root = root.left
         else:
             curnode = list_stack.pop()
             result.append(curnode.val)
             root = curnode.right

     return result

aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.inorderTraversal_ext2, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result'][0]))

# 运行结果
函数 inorderTraversal_ext2 的运行时间为 282.07 ms；内存使用量为 7436.00 KB 执行结果 = 81

---

4. 最优算法

根据本地日志分析，最优算法为第3种方式【迭代遍历】inorderTraversal_ext2

import random
ilen = 1000000
def generate_binary_tree(node_count):
    if node_count <= 0:
        return None
    root = TreeNode(random.randint(1, 100))
    left = generate_binary_tree(node_count // 2)
    right = generate_binary_tree(node_count // 2)
    root.left = left
    root.right = right
    return root
aroot = generate_binary_tree(ilen)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.inorderTraversal_base, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result'][0]))
result = cfp.getTimeMemoryStr(Solution.inorderTraversal_ext1, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result'][0]))
result = cfp.getTimeMemoryStr(Solution.inorderTraversal_ext2, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result'][0]))

# 算法本地速度实测比较
函数 inorderTraversal_base 的运行时间为 654.17 ms；内存使用量为 8284.00 KB 执行结果 = 81
函数 inorderTraversal_ext1 的运行时间为 489.10 ms；内存使用量为 9556.00 KB 执行结果 = 81
函数 inorderTraversal_ext2 的运行时间为 282.07 ms；内存使用量为 7436.00 KB 执行结果 = 81

一日练，一日功，一日不练十日空

may the odds be ever in your favor ~