今天学习了KMP算法。
KMP算法
这是一个字符串查找的算法,我们之前学习的字符串查找都是暴力穷举,然而这个效率太低,于是有三位大佬发明了线性的KMP算法。
算法说难不难,说简单也不简单。
算法的核心思想是找到最长的相等的前缀和后缀,然后可以直接跳到后缀的部分,继续进行比较,让母串的i不回退,从而减少复杂度。
打一个比方:
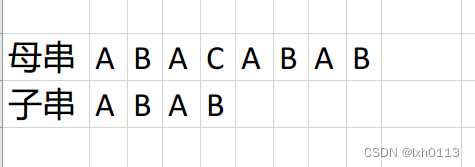
如果子串和母串是上面这个样子,如果用暴力会做一些无用功,因为他到B的位置也一定不同。
当我们比对到3的位置时,最长的前缀和后缀是 A,在4的下标时,就比对不上了。
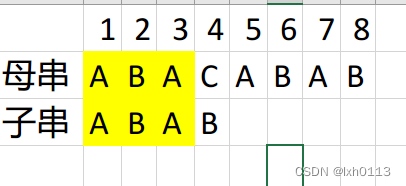
我们可以直接把子串移到3的位置,然后在母串的i 不变,j在4 的位置继续比较,我们发现j在4的位置是不匹配的,这里有一个重点:就是前缀和后缀的长度是不能大于等于前面字符的长度的,前面的长度是1,前缀和后缀恰好都是A,这是不行的。
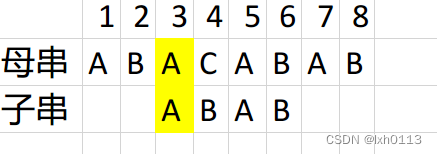
然后就是这样:
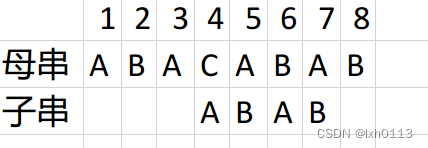
继续往后走:
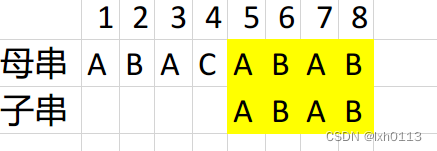
全部匹配。
那么重点来了:我们如何确立我们要跳的距离呢,这里说的是子串的 j位置。
这里就要借助next数组了,next数组存储的是你要跳的距离,next数组是针对子串的,所以next数组应该和子串长度相当,我看过很多博主说过next数组,有些是从1开始存储有些人是从0,有些人next数组下标第一个和第二个存储的是0 1,而有些人不然。我认为,从0 从1全看个人喜好,觉得能够理解就行。
接下来讲一讲next数组如何存放:
当next在1的位置的时候,因为不允许前缀和后缀长度大于等于前面字符的,所以第一个位置是0
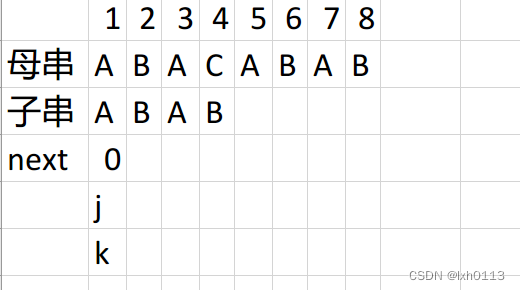
J往后走,此时很明显j的和k的起始位置相比,也就是A和B比较是不相等的,此时next数组2的位置上是0
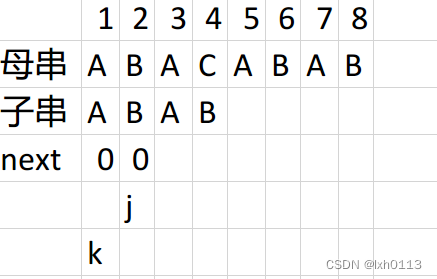
然后j到了3的位置,我们发现j的位置和k位置的字符是相等的,所以我们在next数组3的位置写上1并且k往后走。
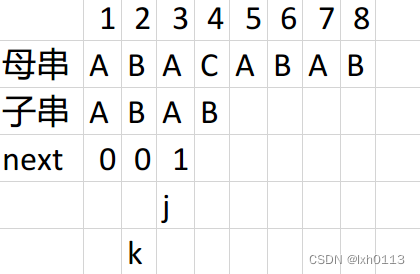
然后j会走到4的位置此时j的位置和k所在的位置是相等的,那么next数组第4个位置的地方存储的是2。
这里还没列出一个特殊情况。
比如:

当继续执行的时候,j++,k++,然后我们发现我们找的是前缀和后缀,此时不相等了,该怎么办,这个时候我们就要执行k=next[k]操作使它回退到A的初始位置1 然后继续比较即可。

这中情况会一直推到1的位置再开始比较。
C语言代码如下:(我代码写的是next数组从0开始存储,这个看个人喜好)
#include<stdio.h>
#define N 200
int js(char a[],int next[])
{
int i,j=0;
next[0]=0;
for(i=1;a[i];)
{
if(a[i]==a[j])
{
j++;
next[i]=j;
i++;
}
else if(j==0)
{
next[i]=j;
i++;
}
else
{
j=next[j];
}
}
}
int kmp(char a[],char b[])
{
int i,j=0;
int next[N]={0};
js(b,next);
for(i=0;a[i];)
{
if(a[i]==b[j])
{
i++;
j++;
}
else if(j==0)
{
i++;
}
else
{
j=next[j-1];
}
if(b[j]==0) return i-j+1;
}
return -1;
}
int main()
{
char str1[N],str2[N];
scanf("%s%s",str1,str2);
printf("%d\n",kmp(str1,str2));
return 0;
}C++代码如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
const int N = 200;
int js(char a[], int next[])
{
int i, j = 0;
next[0] = 0;
for (i = 1; a[i];)
{
if (a[i] == a[j])
{
j++;
next[i] = j;
i++;
} else if (j == 0)
{
next[i] = j;
i++;
} else
{
j = next[j];
}
}
return 0;
}
int kmp(char a[], char b[])
{
int i, j = 0;
int next[N] = {0};
js(b, next);
for (i = 0; a[i];)
{
if (a[i] == b[j])
{
i++;
j++;
}
else if (j == 0)
{
i++;
}
else
{
j = next[j - 1];
}
if (b[j] == 0) return i - j + 1;
}
return -1;
}
int main()
{
char str1[N], str2[N];
cin >> str1 >> str2;
cout << kmp(str1, str2) << endl;
return 0;
}