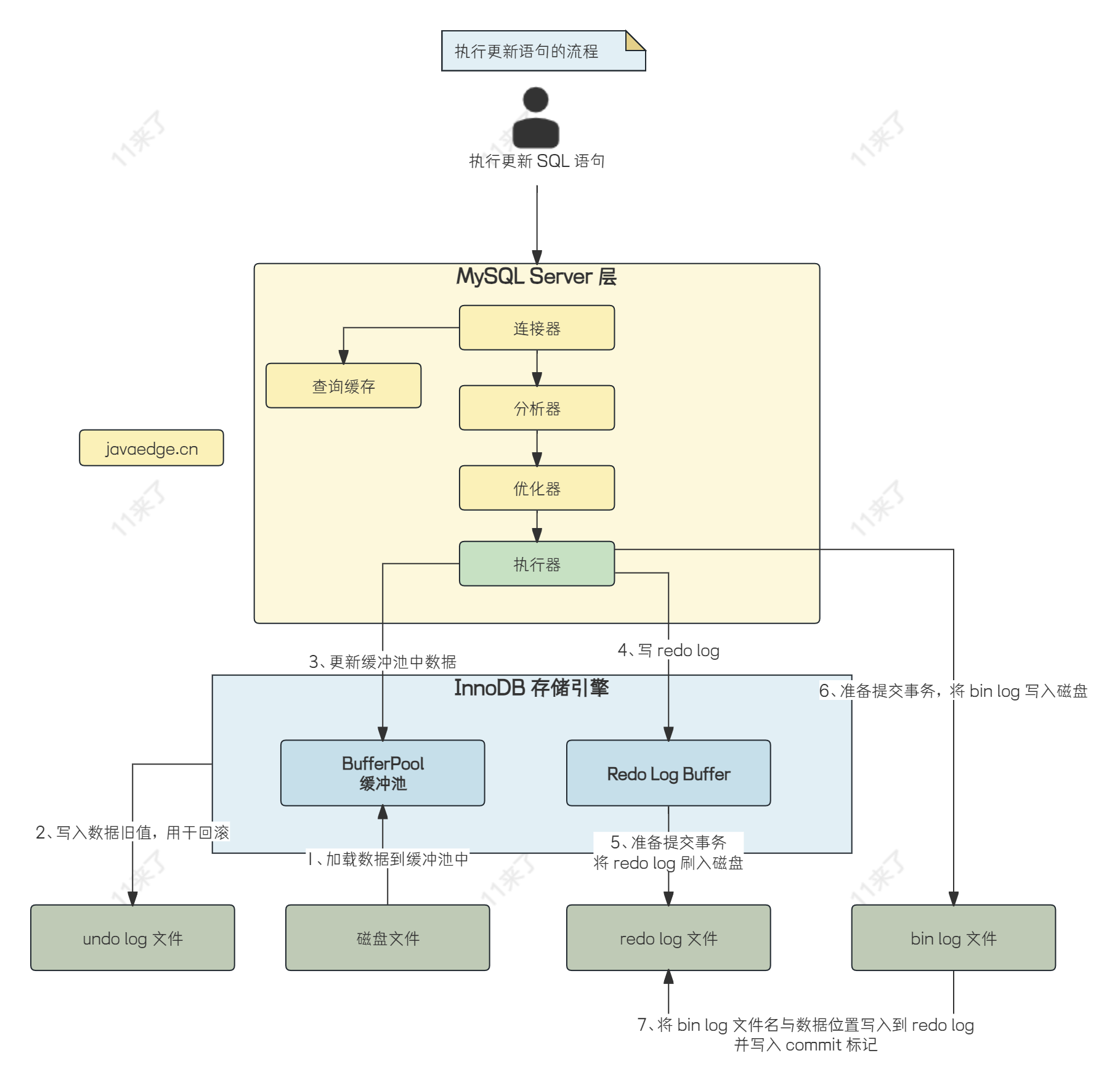
代码随想录Day44 | 完全背包 518 零钱兑换II 377 组合综合IV

完全背包
52.携带研究材料
518.零钱兑换II
377.组合总和Ⅳ

完全背包

文档讲解：代码随想录
视频讲解：
状态

物品的个数是无限个，即一个背包里可以存在同种物品。唯一区别就是遍历顺序。

dp数组
dp[j] 就表示容量为j的背包可以选择价值最大的结果
遍历顺序
我们01背包为什么要从后向前遍历，就是由于从前向后遍历会导致物品重复。所以对于完全背包问题我们对背包的遍历就可以从前向后遍历。
初始化
dp[j] = 0
递推公式
//当j >= 当前要加入物品价值时
dp[j] = max(dp[j],dp[j-weight[i]]+value[i]
打印dp

52.携带研究材料

文档讲解：代码随想录
视频讲解：
状态

本题主要区别就是每个研究材料可以无限选择，那么我们就可以更改遍历顺序，然后更新递推公式就可以求解

#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int N,V;
    cin >> N >> V;
    vector<vector<int>> coll(N,vector<int>(2,0));
    for(int i = 0;i<N;i++)
    {
        cin >> coll[i][0] >> coll[i][1];
    }
    
    //dp数组
    vector<int> dp(V+1,0);
    
    for(int i = 0;i<N;i++)
    {
        for(int j = 0;j<V+1;j++)
        {
            if(j >= coll[i][0])
                dp[j] = max(dp[j],dp[j-coll[i][0]]+coll[i][1]);
        }
    }
    
    cout << dp[V];
    
    return 0;
}

518.零钱兑换II

文档讲解：代码随想录
视频讲解：装满背包有多少种方法？组合与排列有讲究！| LeetCode：518.零钱兑换II
状态

相当于就是容量为amount的背包，从coins物品中选择刚好填满背包有多少种方法

dp数组
dp[j] 表示容量为j的背包有多少种方法填满
递推公式
当j > coins[i]时，dp[j]+=dp[j-coins[i]];
遍历顺序
先物品再背包，重复计算物品背包从前向后
循环是否能够调换–>组合还是排列，这道题的要求显然是组合问题，即不考虑元素顺序对结果的影响。所以不能够调换背包和物品的循环，如果是组合问题，那么就需要考虑顺序影响，那么调换循环的先后就没有关系。
初始化
dp[0] = 1
打印dp数组

//容量为amout的背包，有多少种选择方式
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount+1,0);
        dp[0] = 1;
        for(int i = 0;i<coins.size();i++)
        {
            //背包
            for(int j = 0;j<amount+1;j++)
            {
                if(j >= coins[i])
                {
                    dp[j] += dp[j-coins[i]];
                }
            }
        }
        return dp[amount];
    } 
};

377.组合总和Ⅳ

文档讲解：代码随想录
视频讲解：装满背包有几种方法？求排列数？| LeetCode：377.组合总和IV
状态

本题就属于是排列问题了，使用回溯方法来解决是超时的。
考虑动态规划

dp数组
dp[j]表示的就是对于和为j的话有多少种排列数
递推公式
如果j>nums[i] dp[j] += dp[j-nums[i]]
初始化
dp[0] = 1
遍历顺序
考虑排列，先背包再物品
打印dp

//动态规划
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target+1,0);
        dp[0] = 1;
        for(int j = 0;j<target+1;j++)
        {
            for(int i = 0;i<nums.size();i++)
            {
                if(j >= nums[i] && dp[j] <INT_MAX-dp[j-nums[i]])
                {
                    dp[j] += dp[j-nums[i]];
                }
            }
        }
        return dp[target];
    }
};

给定数组中可能存在两个数相加超过INT的情况