一、题目信息

二、思路分析

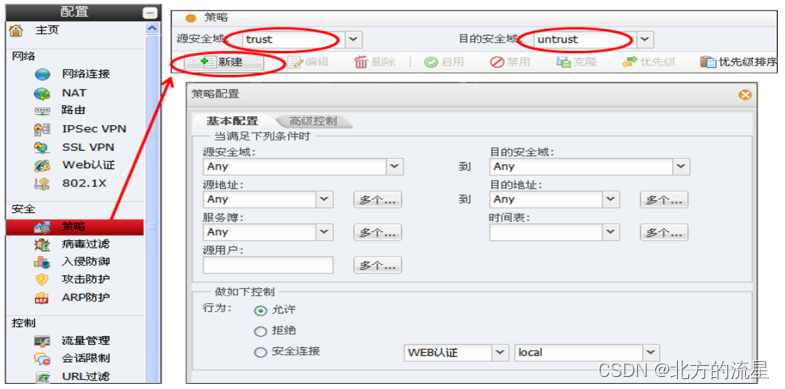
这道题的话，其实只看前一句话，我们应该用的是前缀和算法。但是这道题在此基础上做了改变，我们根据前缀和可以算出排序之前各个区间和的和。

根据题意，我们需要对数组重新排序，使得排序之后区间和的和最大。那么思路很简单，每个区间的和都会使用到这个数组中的元素，区间之间出现交集的话，那么某些元素就会重新使用。所以，我们只需要将出现次数最多的下标位置放我们最大的元素，以此类推。

而这个思路非常像我们之前在贪心章节中所讲解的排队打水问题。

我们假设一个数被用$C_i$次，元素中的元素是$a_i$。那么此时我们所有的区间和加起来的结果可以写成下面这个式子：

$$sum=c_1\ast a_1+c_2\ast a_2+...+c_i\ast a_i$$
这是一个非常经典的，在贪心章节中所讲解的排序不等式。

简单的说，这个不等式的结论就是让最大的出现次数去乘最大的元素。

接下来我们就需要统计一下，每个下标出现的次数。我们准备一个空的数组来记录各个元素的使用次数，如果区间是$[l,r]$。那么意思就是，这个区间里的元素会用到一次，也就是说把我们空数组的这些位置都+1。

而这个过程需要用到的则是和前缀和相反的差分算法。

三、代码实现

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll a[N],s[N],b[N],ms[N];
void insert(int l,int r,int a)
{
    b[l]+=a,b[r+1]-=a;
}
int main()
{
    int n,m;
    cin>>n;
    ll sum_0=0,sum_1=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",a+i);
        s[i]=s[i-1]+a[i];
    }
    cin>>m;
    for(int i=0;i<m;i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        insert(l,r,1);
        sum_0+=s[r]-s[l-1];
    }
    for(int i=1;i<=n;i++)
        b[i]+=b[i-1];
    
    sort(a+1,a+1+n);
    sort(b+1,b+1+n);
    for(int i=1;i<=n;i++)
    {
        sum_1+=(ll)a[i]*b[i];
    }
    cout<<sum_1-sum_0<<endl;
    return 0;
}