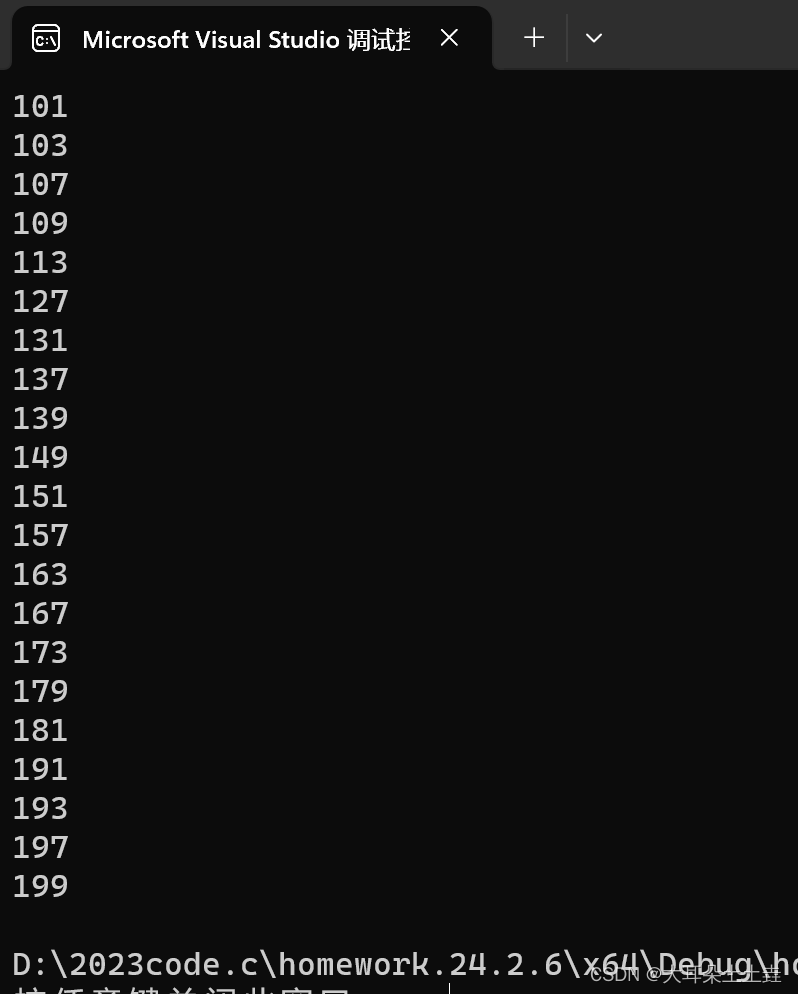
1请编程实现二又树的操作
1.1二又树的创建
1.2二又树的先序遍历
1.3二又树的中序遍历
1.4二又树的后序遍历
1.5二又树各个节点度的个数
1.6二叉树的深度

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <unistd.h>
typedef char datatype;

typedef struct Node
{
	datatype data;//数据域
	struct Node *l;//左孩子
	struct Node *r;//右孩子
}*Btree;
//创建节点
Btree create()
{
	Btree s=(Btree)malloc(sizeof(struct Node));
	if(s==NULL)
	return NULL;
	s->data='\0';
	s->l=NULL;
	s->r=NULL;
	return s;
}
//创建树和插入数据
Btree create_tree()
{
	datatype element;
	printf("please enter element:");
	scanf(" %c",&element);
	if(element=='#')
	{
		return NULL;
	}
	//创建根结点
	Btree tree=create();
	tree->data=element;
	//创建左孩子
	puts("左");
	tree->l=create_tree();
	//创建右孩子
	puts("右");
	tree->r=create_tree();
	//返回主函数
	return tree;
}
//先序遍历输出
void firstoutput(Btree tree)
{
	if(tree==NULL)
		return;
	//输出根
	printf("%c",tree->data);
	//遍历输出左孩子
	firstoutput(tree->l);
	//遍历输出右孩子
	firstoutput(tree->r);
}
//中序遍历输出
void midoutput(Btree tree)
{
	if(tree==NULL)
		return;
	//遍历输出左孩子
	firstoutput(tree->l);
	//输出根
	printf("%c",tree->data);
	//遍历输出右孩子
	firstoutput(tree->r);
}
//后序遍历输出
void lastoutput(Btree tree)
{
	if(tree==NULL)
		return ;
	//遍历输出左孩子
	firstoutput(tree->l);
	//遍历输出右孩子
	firstoutput(tree->r);
	//输出根
	printf("%c",tree->data);
}
//二叉树的各个度的节点个数
void count(Btree tree,int *n0,int *n1,int *n2)
{
	if(tree==NULL)
	return ;
	
	if(!tree->l && !tree->r)
		++*n0;
	else if(tree->l && tree->r)
		++*n2;
	else
		++*n1;
	//遍历左孩子
	count(tree->l,n0,n1,n2);
	//遍历右孩子
	count(tree->r,n0,n1,n2);
}
//计算树深度
int high(Btree tree)
{
	if(tree==NULL)
		return 0;
	//计算左深度
	int left=1+high(tree->l);
	//计算右深度
	int right=1+high(tree->r);
	if(left>right)
		return left;
	else
		return right;
}

int main(int argc, const char *argv[])
{
	//创建二叉树
	Btree tree=create_tree();
	//先序遍历
	printf("先序遍历\n");
	firstoutput(tree);
	puts("");
	//中序遍历输出
	printf("中序遍历\n");
	midoutput(tree);
	puts("");
	//后序遍历输出
	printf("后序遍历\n");
	lastoutput(tree);
	puts("");
	//二插树各个度的结点个数
	int n0=0,n1=0,n2=0;
	count(tree,&n0,&n1,&n2);
	printf("n0=%d n1=%d n2=%d sum=%d\n",n0,n1,n2,n0+n1+n2);
	//计算树的深度
	int len=high(tree);
	printf("二叉树深度为%d\n",len);
	return 0;
}

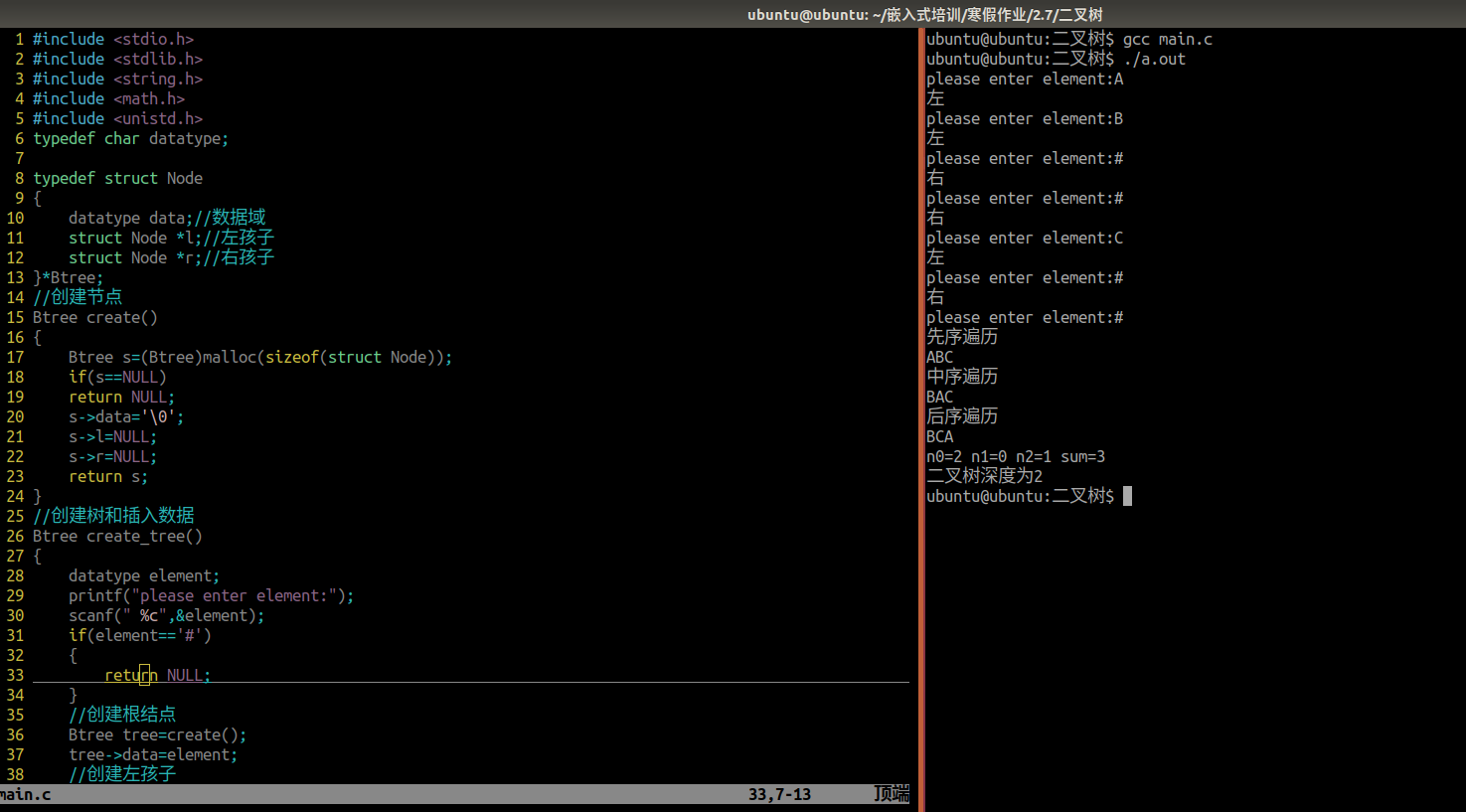
现象展示：